Unit - 2

Context Free Grammar

Q1) Compare RE and CFG?

A1) The difference between RE and CFG

Q2) How to eliminate ambiguity?

A2) Suppose we have a context free grammar G with production rules:

S->aSb|bSa|SS|ɛ

Left most derivation (LMD) and Derivation Tree:

Leftmost derivation of a string from staring symbol S is done by replacing leftmost

Non-terminal symbol by RHS of corresponding production rule.

For example:

The leftmost derivation of string abab from grammar G above is done as:

S =>aSb =>abSab =>abab

The symbols in bold are replaced using production rules.

Derivation tree: It explains how string is derived using production rules from S and

Is shown in Figure.

Fig 1: Derivation tree

Right most derivation (RMD):

It is done by replacing rightmost non-terminal symbol S by RHS of corresponding production rule.

For Example: The rightmost derivation of string abab from grammar G above

Is done as:

S =>SS =>SaSb =>Sab =>aSbab =>abab

The symbols in bold are replaced using production rules.

The derivation tree for abab using rightmost derivation is shown in Figure.

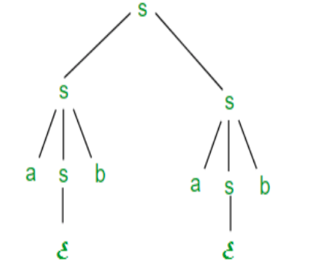
Fig 2: Right most derivation

A derivation can be either LMD or RMD or both or none.

For Example:

S =>aSb =>abSab =>abab is LMD as well as RMD But

S => SS =>SaSb =>Sab =>aSbab =>abab is RMD but not LMD.

Ambiguous Context Free Grammar:

●      A context free grammar is called ambiguous if there exists more than one

LMD or RMD for a string which is generated by grammar.

●      There will also be more than one derivation tree for a string in ambiguous grammar.

●      The grammar described above is ambiguous because there are two derivation Trees.

●      There can be more than one RMD for string abab which are:

S =>SS =>SaSb =>Sab =>aSbab =>abab

S =>aSb =>abSab =>abab

Q3) What is left recursion?

A3) Any non-terminal 'A' whose derivation contains 'A' itself as the left-most symbol makes a grammar left-recursive. For top-down parsers, left-recursive grammar is seen as a difficult scenario. Top-down parsers begin parsing with the Start symbol, which is non-terminal in and of itself. As a result, when the parser encounters the same non-terminal multiple times during its derivation, it becomes difficult for it to determine when to cease parsing the left non-terminal, and it enters an infinite loop.

Example

(1) A => Aα | β

(2) S => Aα | β

A => Sd

(1) is an example of immediate left recursion, where A represents a string of non-terminals and represents any non-terminal symbol.

(2) is an indirect-left recursion example.

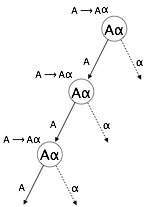
A top-down parser will first parse the A, which will result in a string containing solely of A, and the parser may repeat indefinitely.

Removal of left recursion

The following technique can be used to remove left recursion:

The show's production

A => Aα | β

Is transformed into the following products

A => βA'

A'=> αA' | ε

The strings obtained from the grammar are unaffected, but immediate left recursion is removed.

The following procedure, which should eliminate all direct and indirect left recursions, is the second method.

START

Arrange non-terminals in some order like A1, A2, A3,…, An

For each i from 1 to n

{

For each j from 1 to i-1

{

Replace each production of form Ai ⟹Aj𝜸

With Ai ⟹ δ1𝜸  | δ2𝜸 | δ3𝜸 |…| 𝜸

Where Aj ⟹ δ1 | δ2|…| δn  are current Aj productions

}

}

Eliminate immediate left-recursion

END

Q4) Explain left factoring?

A4) If a common prefix string exists in more than one grammar production rule, the top-down parser is unable to choose which of the production rules to use to parse the string at hand.

Example

When a top-down parser comes across a production like this,

A ⟹ αβ | α𝜸 | …

Because both productions start from the same terminal, it can't decide which one to use to parse the string (or non-terminal). We utilize a method known as left factoring to clear out the ambiguity.

Left factoring modifies the grammar so that top-down parsers can use it. In this method, we build one production for each common prefix and then add more productions to complete the derivation.

Example

The productions listed above can be written in a variety of ways.

A => αA'

A'=> β | 𝜸 | …

The parser now only has one production per prefix, making decision-making easier.

Q5) What regular expression?

A5) Regular expression

​​Simple expressions called Regular Expressions can readily define the language adopted by finite automata. This is the most powerful way of expressing any language.

●      Regular languages are referred to as the languages recognised by certain regular expressions.

●      A regular expression may also be defined as a pattern sequence that defines a series.

●      For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string.

A Regular Expression can be recursively defined as follows −

●      ε is a Regular Expression indicates the language containing an empty

String. (L (ε) = {ε})

●      φ is a Regular Expression denoting an empty language. (L (φ) = { })

●      x is a Regular Expression where L = {x}

●      If X is a Regular Expression denoting the language L(X) and Y is a Regular

●      Expression denoting the language L(Y), then

●      X + Y is a Regular Expression corresponding to the language L(X) ∪

L(Y) where L(X+Y) = L(X) ∪ L(Y).

●      X . Y is a Regular Expression corresponding to the language L(X) .

L(Y) where L(X.Y) = L(X) . L(Y)

●      R* is a Regular Expression corresponding to the language L(R*)

Where L(R*) = (L(R))*

●      If we apply any of the rules several times from 1 to 5, they are Regular

Expressions.

Unix Operator Extensions

Regular expressions are used frequently in Unix:

●      In the command line

●      Within text editors

●      In the context of pattern matching programs such as grep and egrep

Additional operators are recognized by unix. These operators are used for

Convenience only.

●      character classes: ‘[‘ <list of chars> ‘]’

●      start of a line: ‘^’

●      end of a line: ‘$’

●      wildcard matching any character except newline: ‘.’

●      optional instance: R? = epsilon | R

●      one or more instances: R+ == RR*

Q6) What is context free grammar?

A6) Context free grammar

Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.

It consists of:

●      a set of terminal symbols,

●      a set of non-terminal symbols,

●      a set of productions,

●      a start symbol.

Context-free grammar G can be defined as:

G = (V, T, P, S)

Where 

G - grammar, used for generate string,

V - final set of non-terminal symbol, which are denoted by capital letters,

T - final set of terminal symbols, which are denoted be small letters,

P - set of production rules, it is used for replacing non terminal symbol of a string in both side (left or right)

S - start symbol, which is used for derive the string

A CFG for Arithmetic Expressions -

An example grammar that generates strings representing arithmetic expressions with the four operators +, -, *, /, and numbers as operands is:

1. <expression> --> number

2. <expression> --> (<expression>)

3.<expression> --> <expression> +<expression>

4. <expression> --> <expression> - <expression>

5. <expression> --> <expression> * <expression>

6. <expression> --> <expression> / <expression>

The only non-terminal symbol in this grammar is <expression>, which is also the

Start symbol. The terminal symbols are {+, -, *, /, (, ), number}

●      The first rule states that an <expression> can be rewritten as a number.

●      The second rule says that an <expression> enclosed in parentheses is also an <expression>

●      The remaining rules say that the sum, difference, product, or division of two <expression> is also an expression.

Q7) Do left factoring in the following grammar - S → iEtS / iEtSeS / a?

A7) The left factored grammar is-

S → iEtSS’ / a

S’ → eS / ∈

E → b

Q8) Do left factoring in the following grammar - A → aAB / aBc / aAc?

A8) Step-01:

A → aA’

A’ → AB / Bc / Ac

Again, this is a grammar with common prefixes.

Step-02:

A → aA’

A’ → AD / Bc

D → B / c

This is a left factored grammar.

Q9) Do left factoring in the following grammar - S → bSSaaS / bSSaSb / bSb / a?

A9) Step-01:

S → bSS’ / a

S’ → SaaS / SaSb / b

Again, this is a grammar with common prefixes.

Step-02:

S → bSS’ / a

S’ → SaA / b

A → aS / Sb

This is a left-factored grammar.

Q10) Do left factoring in the following grammar - S → aSSbS / aSaSb / abb / b?

A10) Step-01:

S → aS’ / b

S’ → SSbS / SaSb / bb

Again, this is a grammar with common prefixes.

Step-02:

S → aS’ / b

S’ → SA / bb

A → SbS / aSb

This is a left-factored grammar.

Q11) Do left factoring in the following grammar - S → a / ab / abc / abcd?

A11) Step-01:

S → aS’

S’ → b / bc / bcd / ∈

Again, this is a grammar with common prefixes.

Step-02:

S → aS’

S’ → bA / ∈

A → c / cd / ∈

Again, this is a grammar with common prefixes.

Step-03:

S → aS’

S’ → bA / ∈

A → cB / ∈

B → d / ∈

This is a left factored grammar.

Q12) Consider the following grammar and eliminate left recursion-

A → ABd / Aa / a

B → Be / b

A12) The grammar after eliminating left recursion is-

A → aA’

A’ → BdA’ / aA’ / ∈

B → bB’

B’ → eB’ / ∈

Q13) Consider the following grammar and eliminate left recursion - E → E + E / E x E / a?

A13) The grammar after eliminating left recursion is-

E → aA

A → +EA / xEA / ∈

Q14) Consider the following grammar and eliminate left recursion-

E → E + T / T

T → T x F / F

F → id

A14) The grammar after eliminating left recursion is-

E → TE’

E’ → +TE’ / ∈

T → FT’

T’ → xFT’ / ∈

F → id

Q15) Consider the following grammar and eliminate left recursion-

S → (L) / a

L → L, S / S

A15) The grammar after eliminating left recursion is-

S → (L) / a

L → SL’

L’ → ,SL’ / ∈

Q16) Consider the following grammar and eliminate left recursion-

S → S0S1S / 01

A16) The grammar after eliminating left recursion is-

S → 01A

A → 0S1SA / ∈

Q17) Consider the following grammar and eliminate left recursion-

S → A

A → Ad / Ae / aB / ac

B → bBc / f

A17) The grammar after eliminating left recursion is-

S → A

A → aBA’ / acA’

A’ → dA’ / eA’ / ∈

B → bBc / f

Q18) Consider the following grammar and eliminate left recursion-

A → Ba / Aa / c

B → Bb / Ab / d

A18) This is a case of indirect left recursion.

Step-01:

First let us eliminate left recursion from A → Ba / Aa / c

Eliminating left recursion from here, we get-

A → BaA’ / cA’

A’ → aA’ / ∈

Now, given grammar becomes-

A → BaA’ / cA’

A’ → aA’ / ∈

B → Bb / Ab / d

Step-02:

Substituting the productions of A in B → Ab, we get the following grammar-

A → BaA’ / cA’

A’ → aA’ / ∈

B → Bb / BaA’b / cA’b / d

Step-03:

Now, eliminating left recursion from the productions of B, we get the following grammar-

A → BaA’ / cA’

A’ → aA’ / ∈

B → cA’bB’ / dB’

B’ → bB’ / aA’bB’ / ∈

This is the final grammar after eliminating left recursion.

Q19) Consider the following grammar and eliminate left recursion-

X → XSb / Sa / b

S → Sb / Xa / a

A19) This is a case of indirect left recursion.

Step-01:

First let us eliminate left recursion from X → XSb / Sa / b

Eliminating left recursion from here, we get-

X → SaX’ / bX’

X’ → SbX’ / ∈

Now, given grammar becomes-

X → SaX’ / bX’

X’ → SbX’ / ∈

S → Sb / Xa / a

Step-02:

Substituting the productions of X in S → Xa, we get the following grammar-

X → SaX’ / bX’

X’ → SbX’ / ∈

S → Sb / SaX’a / bX’a / a

Step-03:

Now, eliminating left recursion from the productions of S, we get the following grammar-

X → SaX’ / bX’

X’ → SbX’ / ∈

S → bX’aS’ / aS’

S’ → bS’ / aX’aS’ / ∈

This is the final grammar after eliminating left recursion.

Q20) Consider the following grammar and eliminate left recursion-

S → Aa / b

A → Ac / Sd / ∈

A20) This is a case of indirect left recursion.

Step-01:

First let us eliminate left recursion from S → Aa / b

This is already free from left recursion.

Step-02:

Substituting the productions of S in A → Sd, we get the following grammar-

S → Aa / b

A → Ac / Aad / bd / ∈

Step-03:

Now, eliminating left recursion from the productions of A, we get the following grammar-

S → Aa / b

A → bdA’ / A’

A’ → cA’ / adA’ / ∈

This is the final grammar after eliminating left recursion.