Unit - 5
Intermediate code generation
Q1) What is an intermediate representation?
A1) Intermediate language
Intermediate representation in three ways:
- Syntax tree
The syntax tree is nothing more than a condensed parse tree shape. The parse tree operator and keyword nodes are transferred to their parents, and in the syntax tree the internal nodes are operators and child nodes are operands, a chain of single productions is replaced by a single connection. Put parentheses in the expression to shape the syntax tree, so it is simple to identify which operand should come first.
Example –
x = (a + b * c) / (a – b * c )
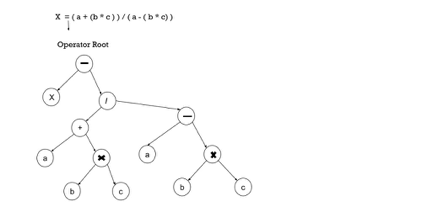
Fig 1: Syntax tree
2. Postfix notation
The standard way to write the sum of a and b is with the operator in the middle: a + b
For the same expression, the postfix notation positions the operator as ab + at the right end. In general, the consequence of adding + to the values denoted by e1 and e2 is postfix notation by e1e2 +, if e1 and e2 are any postfix expressions, and + is any binary operator.
In postfix notation, no parentheses are needed because the location and arity (number of arguments) of the operators enable only one way of decoding a postfix expression. The operator obeys the operand in postfix notation.
Example –
Representation of a phrase by postfix (a – b) * (c + d) + (e – f) is :
Ab – cd + *ef -+.
3. Three address code
Three address statements are defined as a sentence that contains no more than three references (two for operands and one for outcomes). Three address codes are defined as a series of three address statements. The type x = y op z is a three address statement, where x, y, z would have an address (memory location). A statement may often contain fewer than three references, but it is still considered a statement of three addresses.
Example –
The code of the three addresses for the phrase: a + b * c + d :
T 1 = b * c
T 2 = a + T 1
T 3 = T 2 + d
T 1, T 2, T 3 are temporary variables.
Advantages of three address code
● For target code generation and optimization, the unravelling of complex arithmetic expressions and statements makes the three-address code ideal.
● Using names for the intermediate values determined by a programme makes it easy to rearrange the three-address code - unlike postfix notation.
Q2) Write the synthesized and inherited attributes?
A2) Synthesized Attributes
A Synthesized attribute is an attribute of the non-terminal on the left-hand side of a production. Synthesized attributes represent information that is being passed up the parse tree. The attribute can take value only from its children (Variables in the RHS of the production).
For eg. Let’s say A -> BC is a production of a grammar, and A’s attribute is dependent on B’s attributes or C’s attributes then it will be a synthesized attribute.
Inherited attributes
An attribute of a nonterminal on the right-hand side of a production is called an inherited attribute. The attribute can take value either from its parent or from its siblings (variables in the LHS or RHS of the production).
For example, let’s say A -> BC is a production of a grammar and B’s attribute is dependent on A’s attributes or C’s attributes then it will be an inherited attribute.
Q3) Explain dependency graph?
A3) A dependency graph depicts the flow of information among the attribute instances in a particular parse tree; an edge from one attribute instance to another means that the value of the first is needed to compute the second. Edges express constraints implied by the semantic rules. In more detail:
● For each parse-tree node, say a node labeled by grammar symbol X , the dependency graph has a node for each attribute associated with X .
● Suppose that a semantic rule associated with a production p defines the value of synthesized attribute A.b in terms of the value of X.c (the rule may define A.b in terms of other attributes in addition to X.c). Then, the dependency graph has an edge from X.c to A.b. More precisely, at every node N labeled A where production p is applied, create an edge to attribute b at N, from the attribute c at the child of N corresponding to this instance of the symbol X in the body of the production.
Since a node N can have several children labeled X, we again assume that subscripts distinguish among uses of the same symbol at different places in the production.
● Suppose that a semantic rule associated with a production p defines the value of inherited attribute B.c in terms of the value of X.a. Then, the dependency graph has an edge from X.a to B.c.
● For each node N labeled B that corresponds to an occurrence of this B in the body of production p, create an edge to attribute c at N from the attribute a at the node M that corresponds to this occurrence of X. Note that M could be either the parent or a sibling of N.
Q4) Describe syntax directed transition?
A4) In syntax-directed translation, certain informal notations are associated with the grammar and these notations are called semantic rules.
Therefore, we may say that
Grammar + semantic rule = SDT (syntax directed translation)
● In syntax-directed translation, depending on the form of the attribute, each non-terminal may get one or more attributes, or sometimes 0 attributes.
● Semantic rules aligned with the output rule determine the value of these attributes.
● Whenever a construct meets in the programming language in Syntax driven translation, it is translated according to the semantic rules specified in that particular programming language.
Example:
Production | Semantic rule |
E → E + T | E.val := E.val + T.val |
E → T | E.val := T.val |
T → T * F | T.val := T.val + F.val |
T → F | T.val := F.val |
F → (F) | F.val := F.val |
F → num | F.val := num.lexval |
One of E's attributes is E.val.
The attribute returned by the lexical analyser is num.lexval.
Implementation of syntax directed translation
By building a parse tree and performing the acts first order in a left to right depth, syntax directed translation is implemented.
Syntax Directed Translation is an improved grammar law that makes semantic analysis easier. In the form of attributes attached to the nodes, SDT requires moving data bottom-up and/or top-down to the parse tree.
Syntax Directed translation rules use, in their meanings,
1) lexical values of nodes,
2) constants &
3) attributes associated with non-terminals.
The general approach to Syntax-Directed Translation is to create a parse tree or syntax tree and, by visiting them in some order, compute the attribute values at the nodes of the tree. In certain instances, without creating an explicit tree, translation can be achieved during parsing.
Example
Production | Semantic rule |
S → E $ | { printE.VAL } |
E → E + E | {E.VAL := E.VAL + E.VAL } |
E → E * E | {E.VAL := E.VAL * E.VAL } |
E → (E) | {E.VAL := E.VAL } |
E → I | {E.VAL := I.VAL } |
I → I digit | {I.VAL := 10 * I.VAL + LEXVAL } |
I → digit | { I.VAL:= LEXVAL} |
Parse tree for SDT:
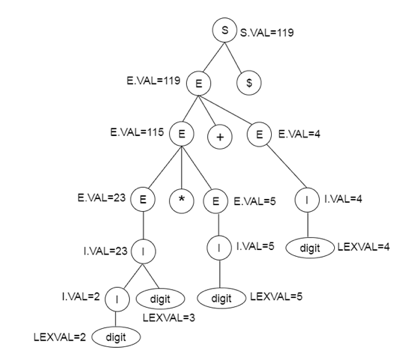
Fig 2: Parse tree for SDT
Q5) Define S and L attributed?
A5) S-attributed SDT refers to an SDT that solely employs synthesized attributes. S-attributed SDTs with their semantic actions written after the production are used to evaluate these characteristics (right hand side).
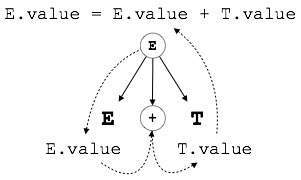
Fig 3: s attribute
As shown above, attributes in S-attributed SDTs are assessed via bottom-up parsing because the parent node values are dependent on the child node values.
L - attributed definitions
L-Attributed definitions are the L-Attribute class of Syntax Directed Definitions (SDD). The logic behind this class is that dependency-graph edges between attributes linked with a production body can go from left to right, but not right to left, therefore L-attribute.
Attribute grammars of the type L are a subset of attribute grammars. They allow the attributes to be assessed in a single left-to-right traversal of the SDD from depth to right. As a result, top-down parsing can easily incorporate attribute evaluation in L-attributed grammars.
Many computer languages have the letter L attached to them. Narrow compilers are special types of compilers that use some form of L-attributed grammar. S-attributed grammars are a strict superset of these. It's used to make code.
A non-terminal in a L-attributed SDT can obtain values from its parent, child, and sibling nodes.
Example:
Let following production
S -->ABC
S is capable of taking values from A, B, and C. (synthesized). A can only take values from S. B is able to take values from both S and A. S, A, and B can all provide values to C.
No non-terminal can obtain values from its right-hand sibling.
The depth-first and left-to-right parsing method is used to assess attributes in L-attributed SDTs.
Fig 4: S and L attribute definitions
Q6) What are polish notations?
A6) If the language given is expressions, the Postfix notation is a useful type of intermediate code.
● Postfix notation is sometimes referred to as 'reverse polish' and 'suffix notation'.
● A linear representation of a syntax tree is the Postfix notation.
● Any expression can be written unambiguously without parentheses in the postfix notation.
● The ordinary way (infix) to write the number of a and b is with the middle operator: a * b. In the postfix notation, however, we position the operator as ab * at the right end.
● The operator obeys the operand in postfix notation.
Q7) Write any example of polish notation?
A7) Production
- E → E1 op E2
- E → (E1)
- E → id
Semantic rule | Program fragment |
E.code = E1.code || E2.code || op | Print op |
E.code = E1.code |
|
E.code = id | Print id |
Example:
a := b * -c + b * -c
Postfix notation of given above statement:
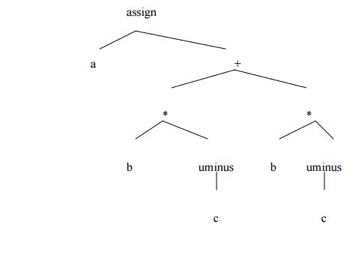
Fig 5: Postfix notation
Q8) What are quadruples?
A8) Quadruple
For the implementation of the three address codes, the quadruples have four fields. The quadruple field includes the name of the generator, the first operand source, the second operand source, and the output, respectively
Operator |
Argument 1 |
Argument 2 |
Destination |
Table: Quadruple field
Example
w := -x * y + z
The code with three addresses is as follows:
t1 := -x
t2 := y + z
t3 := t1 * t2
w := t3
These statements are expressed as follows by quadruples:
| Operator | Source 1 | Source 2 | Destination |
(0) | Uminus | x |
| t1 |
(1) | + | y | z | t2 |
(2) | * | t1 | t2 | t3 |
(3) | := | t3 |
| w |
Q9) What are triples?
A9) For the implementation of the three address code, the triples have three fields. The area of triples includes the name of the operator, the first operand of the source and the second operand of the source.
The outcomes of the respective sub-expressions are denoted by the expression location in triples. Although describing expressions, Triple is equal to DAG.
Operator |
Argument 1 |
Argument 2 |
Table: Triples field
Example:
w := -x * y + z
The three code addresses are as follows:
t1 := -x
t2 := y + zM
t3 := t1 * t2
w := t3
Triples represent these statements as follows:
| Operator | Source 1 | Source 2 |
(0) | Uminus | x |
|
(1) | + | y | z |
(2) | * | (0) | (1) |
(3) | := | (2) |
|
Q10) What are indirect triples?
A10) This is a better representation than the triples representation.
● It lists the pointers to the triples in the desired order using an additional instruction array.
● As a result, pointers are employed to store the results instead of positions.
● It enables optimizers to quickly reposition the sub-expression in order to generate optimal code.
The goto declaration modifies the control stream. We need to specify a LABEL for a statement if we enforce Goto statements. To this end, an output may be added:
S → LABEL : S
LABEL → id
Semantic action is attached to this production device to record the Mark and its meaning in the symbol table.
The following grammar is used to integrate flow-of-control structure constructs:
S → if E then S
S → if E then S else S
S → while E do S
S → begin L end
S→ A
L→ L ; S
L → S
S is a statement here, L is a statement-list, A is an assignment statement, and E is an expression valued by Boolean.
Q11) Write the Translation scheme for a statement that alters flow of controls?
A11) Translation scheme for statement that alters flow of controls
● As in the case of Boolean expression grammar, we add the marker non-terminal M.
● If so, this M is put before the statement in both. We need to put M before E in the case of while-do, as we need to return to it after executing S.
● If we test E to be valid in the case of if-then-else, first S will be executed.
● After this, we can make sure that the code after the if-then else is executed instead of the second S. Then, after first S, we put another non-terminal marker of N.
Grammar:
S → if E then M S
S → if E then M S else M S
S → while M E do M S
S → begin L end
S → A
L→ L ; M S
L → S
M → ∈
N → ∈
For this grammar, the translation scheme is as follows:
Production rule | Semantic action |
S → if E then M S1 | BACKPATCH (E.TRUE, M.QUAD) S.NEXT = MERGE (E.FALSE, S1.NEXT) |
S → if E then M1 S1 else M2 S2 | BACKPATCH (E.TRUE, M1.QUAD) BACKPATCH (E.FALSE, M2.QUAD) S.NEXT = MERGE (S1.NEXT, N.NEXT, S2.NEXT) |
S → while M1 E do M2 S1 | BACKPATCH (S1,NEXT, M1.QUAD) BACKPATCH (E.TRUE, M2.QUAD) S.NEXT = E.FALSE GEN (goto M1.QUAD) |
S → begin L end | S.NEXT = L.NEXT |
S → A | S.NEXT = MAKELIST () |
L → L ; M S | BACKPATHCH (L1.NEXT, M.QUAD) L.NEXT = S.NEXT |
L → S | L.NEXT = S.NEXT |
M → ∈ | M.QUAD = NEXTQUAD |
N→ ∈ | N.NEXT = MAKELIST (NEXTQUAD) GEN (goto_) |
Q12) Translate the following expression to quadruple, triple and indirect triple- a + b x c / e ↑ f + b x c?
A12) Three Address Code for the given expression is-
T1 = e ↑ f
T2 = b x c
T3 = T2 / T1
T4 = b x a
T5 = a + T3
T6 = T5 + T4
Now, we write the required representations-
Quadruple Representation-
Location | Op | Arg1 | Arg2 | Result |
(0) | ↑ | e | f | T1 |
(1) | x | b | c | T2 |
(2) | / | T2 | T1 | T3 |
(3) | x | b | a | T4 |
(4) | + | a | T3 | T5 |
(5) | + | T5 | T4 | T6 |
Triple representations
Location | Op | Arg1 | Arg2 |
(0) | ↑ | e | f |
(1) | x | b | c |
(2) | / | (1) | (0) |
(3) | x | b | a |
(4) | + | a | (2) |
(5) | + | (4) | (3) |
Indirect triple representation
Statement |
|
35 | (0) |
36 | (1) |
37 | (2) |
38 | (3) |
39 | (4) |
40 | (5) |
Location | Op | Arg1 | Arg2 |
(0) | ↑ | e | f |
(1) | x | b | e |
(2) | / | (1) | (0) |
(3) | x | b | a |
(4) | + | a | (2) |
(5) | + | (4) | (3) |
Q13) Translate the following expression to quadruple, triple and indirect triple - a = b x – c + b x – c?
A13) Three Address Code for the given expression is-
T1 = uminus c
T2 = b x T1
T3 = uminus c
T4 = b x T3
T5 = T2 + T4
a = T5
Now, we write the required representations-
Quadruple Representation-
Location | Op | Arg1 | Arg2 | Result |
(1) | Uminus | c |
| T1 |
(2) | x | b | T1 | T2 |
(3) | Uminus | c |
| T3 |
(4) | x | b | T3 | T4 |
(5) | + | T2 | T4 | T5 |
(6) | = | T5 |
| a |
Triple Representation-
Location | Op | Arg1 | Arg2 |
(1) | Uminus | c |
|
(2) | x | b | (1) |
(3) | Uminus | c |
|
(4) | x | b | (3) |
(5) | + | (2) | (4) |
(6) | = | a | (5) |
Indirect Triple Representation-
| Statement |
35 | (1) |
36 | (2) |
37 | (3) |
38 | (4) |
39 | (5) |
40 | (6) |
Location | Op | Arg1 | Arg2 |
(1) | Uminus | c |
|
(2) | x | b | (1) |
(3) | Uminus | c |
|
(4) | x | b | (3) |
(5) | + | (2) | (4) |
(6) | = | a | (5) |
Q14) Write Three Address Code for the following expression - a = b + c + d?
A14) The given expression will be solved as-
Three Address Code for the given expression is-
(1) T1 = b + c
(2) T2 = T1 + d
(3) a = T2
Q15) Write Three Address Code for the following expression -- (a x b) + (c + d) – (a + b + c + d)?
A15) Three Address Code for the given expression is-
(1) T1 = a x b
(2) T2 = uminus T1
(3) T3 = c + d
(4) T4 = T2 + T3
(5) T5 = a + b
(6) T6 = T3 + T5
(7) T7 = T4 – T6
Q16) Write Three Address Code for the following expression - If A < B then 1 else 0?
A16) Three Address Code for the given expression is-
(1) If (A < B) goto (4)
(2) T1 = 0
(3) goto (5)
(4) T1 = 1
Q17) Write Three Address Code for the following expression - If A < B and C < D then t = 1 else t = 0?
A17) Three Address Code for the given expression is-
(1) If (A < B) goto (3)
(2) goto (4)
(3) If (C < D) goto (6)
(4) t = 0
(5) goto (7)
(6) t = 1