Unit – 1
Function of one variable
Q1) What is Leibnitz’s theorem?
A1)
Successive differentiation-
The successive differential coefficients of y are denoted as follows-
 ……………….
……………….
The 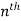 differential coefficient is-
differential coefficient is- 
Statements of Leibnitz’s Theorem-
If u and v are the function of x such that their nth derivative exists, then the nth derivative of their product will be
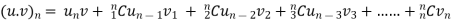
Q2) What is nth derivative of 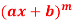 ?
?
A2)
Suppose y = 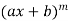
Differentiate with respect to x successively, we get

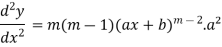

For n times differentiation, we get-
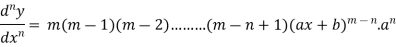
So we can say that its n’th derivative will be
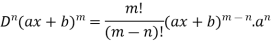
Q3) Find the nth derivative of sin(ax + b).
A3)
Suppose y = sin(ax + b)
Differentiate with respect to x successively, we get
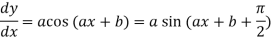
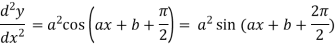

For n times differentiation, we get-

So we can say that its n’th derivative will be
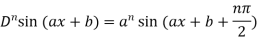
Q4) If y = l , then show that-
, then show that-
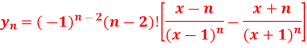
A4)
We have,
y = 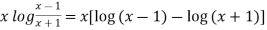
Differentiate y with respect to x, we get
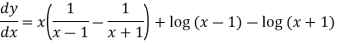
= 
Again diff. (n – 1) times w.r .t x , we get-
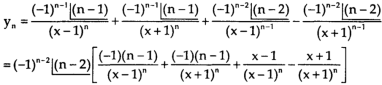
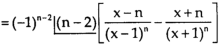
Q5) Find cos x cos 2x cos 3x.
A5)
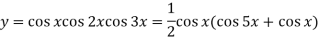
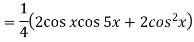
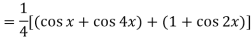
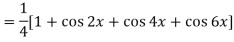
So that-
n’th derivative-
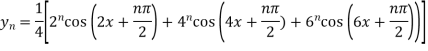
Q6) Find the  derivative of the following function-
derivative of the following function-
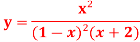
A6)
Partial fraction of the function y after splitting-
Suppose x – 1 = z, then

= 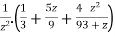
= 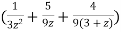
= 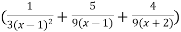
Here we can find its n’th derivative-
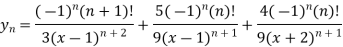
Q7) Find 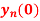 if
if 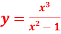
A7)
Here we have-
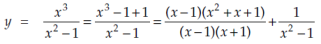
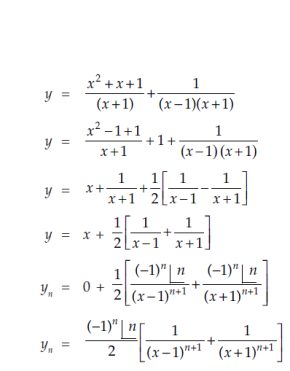
At x = 0,

When n is odd-
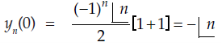
When n is even
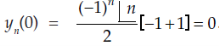
Q8) Find the nth derivative of sin3 x.
A8)
We know that sin 3x= 3sin x 4sin3 x = sin3x = 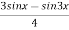
Differentiate n times w.r.t x,
 ( sin3 x) =
( sin3 x) = 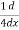 (3 sinx- sin3x)
(3 sinx- sin3x)
= ( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
Q9) If y= e-kx/2(a cosnx+ b sinnx) then show that.,y2+ ky1+(n2+ k2/4)y =0.
A9)
y= e-kx/2(a cosnx+ b sinnx)
Differentiating w.r.to. x.,
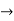 Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
 Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx)
Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx) 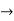 (1)
(1)
Differentiating w.r.to x.,
Y2+ k/2.y1 = ne-kx/2 (-k/2) ( -an sin nx + bn cos nx) + n e-kx/2(-an cosnx- bn sinnx).
= -(k/2) (y1+ k/2 y)- n2 y = - (k/2 y1)- ( k2/4)y- n2y.
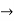 y2 + ky1 +(n2+ k2/4)y = 0.
y2 + ky1 +(n2+ k2/4)y = 0.
Q10) If y  , then prove that-
, then prove that-
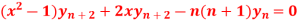
A10)
Here it is given that-
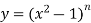
On differentiating-
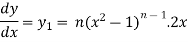
Or
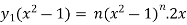
= ny.2x
Differentiate again with respect to x, we get-
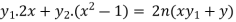
Or
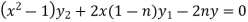 …………………. (1)
…………………. (1)
Differentiate each term of (1) by using Leibnitz’s theorem, we get-
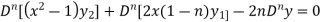
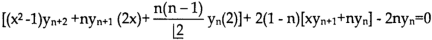
Therefore we get-
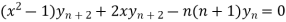
Hence proved.
Q11) If y =  , then prove that-
, then prove that-
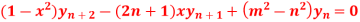
A11)
It is given that- y = 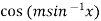
First derivative –
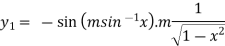
It becomes-
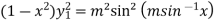
= 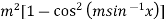
= 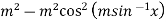
= 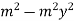
Becomes-
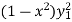 +
+ 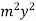 -
- 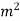 = 0
= 0
Om differentiating again we get-
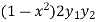 +
+ 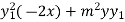 = 0
= 0
Or
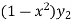 +
+  = 0
= 0
Differentiate n times by using Leibnitz’s theorem, we get-
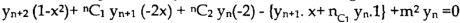
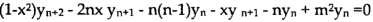
So that

Hence proved.
Q12) If  , then show that
, then show that
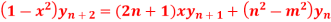
A12)
Also, find 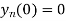
Here 
Differentiating with respect to x, we get
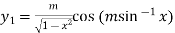 …(ii)
…(ii)
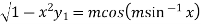
Squaring both side we get
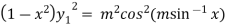
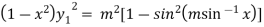
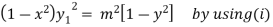
 …(iii)
…(iii)
Again differentiating with respect to x ,we get
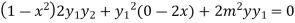
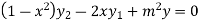
Using Leibnitz’s theorem we get
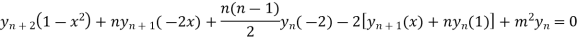

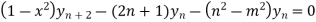 …(iv)
…(iv)
Putting x=0 in equation (i),(ii) and (iii) we get
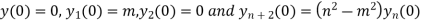
Putting n=1,2,3,4….
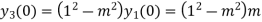
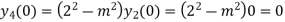
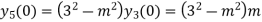
………………
Hence 
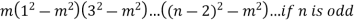
Q13) What is Maclaurin’s theorem.
A13)
Maclaurin’s series-
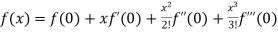 + …….
+ …….
Which is called Maclaurin’s theorem.
Note – if we put h = x - a then there will be the expansion of F(x) in powers of (x – a)
We get-
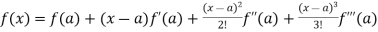 + ……
+ ……
Q14) Expand 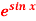 by using Maclaurin’s series.
by using Maclaurin’s series.
A14)
Let

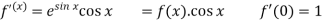
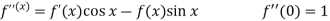
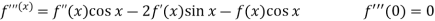
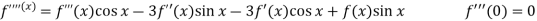
Put these values in Maclaurin’s series-
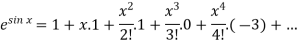
Or
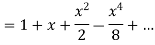
Q15) Expand 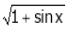 upto x6
upto x6
A15)
Here 

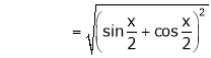
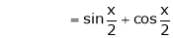
Now we know that
 … (1)
… (1)
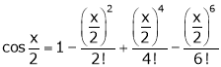 … (2)
… (2)
Adding (1) and (2) we get

Q16) Expand  in power of (x – 3)
in power of (x – 3)
A16)
Let 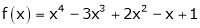
Here a = 3
Now by Taylor’s series expansion,
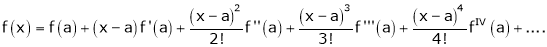 … (1)
… (1)
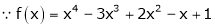

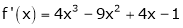
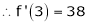

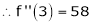
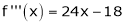
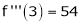
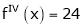
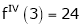
 equation (1) becomes.
equation (1) becomes.
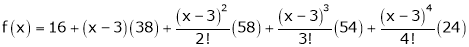
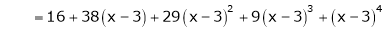
Q17) Using Taylors series method expand 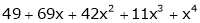 in powers of (x + 2)
in powers of (x + 2)
A17)
Here 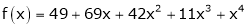
a = -2
 By Taylors series,
By Taylors series,
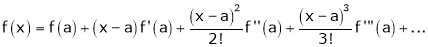 … (1)
… (1)
Since
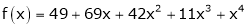
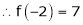
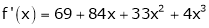
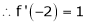
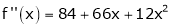
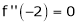
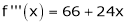

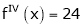
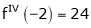 ,
, 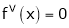 , …..
, …..
Thus equation (1) becomes

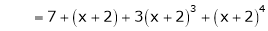
Q18) Using Taylors series method expand 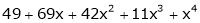 in powers of (x + 2).
in powers of (x + 2).
A18)
Here 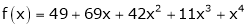
a = -2
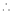 By Taylors series,
By Taylors series,
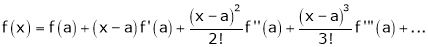 … (1)
… (1)
Since
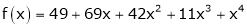
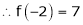
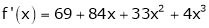
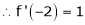
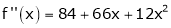
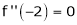

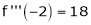
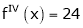
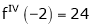 ,
,  , …..
, …..
Thus equation (1) becomes
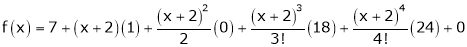
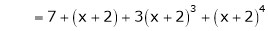
Q19) Evaluate 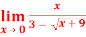
A19)
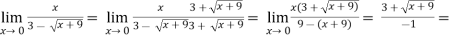 -6.
-6.
Q20) Calculate 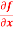 and
and 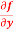 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
A20)
To calculate 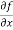 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
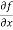 =
= 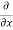 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
=  3x³] -
3x³] - 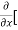 5y²] +
5y²] + 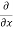 [2xy] -
[2xy] -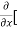 8x] +
8x] +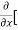 4y] -
4y] - 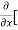 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
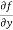 =
=  [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
=  3x³] -
3x³] -  5y²] +
5y²] + 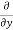 [2xy] -
[2xy] -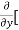 8x] +
8x] +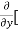 4y] -
4y] - 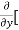 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Q21) Calculate 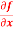 and
and  for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
A21)
To calculate  treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
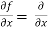 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8) (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50)cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
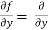 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)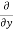 (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xy cos(y²x + 5x – 8)
Q22) if  , then show that-
, then show that- 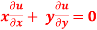
A22)
Here we have,
u = 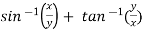 …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get

= 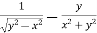
Or
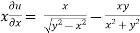 ………………..(2)
………………..(2)
And now,
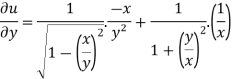
= 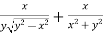
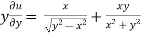 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
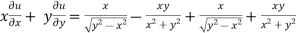 = 0
= 0
Hence proved.
Q23) If 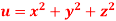 where
where  then find the value of
then find the value of 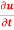 ?
?
A23)
Given 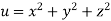
Where 
By chain rule
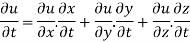
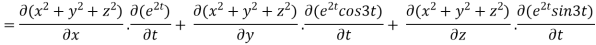
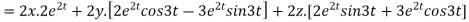
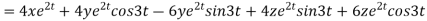
Now substituting the value of x ,y,z we get
 -6
-6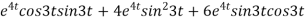
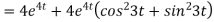
 8
8
Q24) If 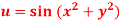 where the relation is
where the relation is  .
.
Find the value of 
A24)
Let the given relation is denoted by 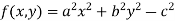
We know that 
Differentiating u with respect to x and using chain rule
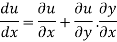
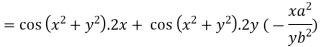
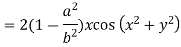
Q25) State and prove Euler’s theorem.
A25)
Statement – if u = f(x, y) be a homogeneous function in x and y of degree n , then
x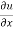 + y
+ y  = nu
= nu
Proof: Here u is a homogeneous function of degree n,
u = xⁿ f(y/x) ----------------(1)
Partially differentiate equation (1) with respect to x,
 = n
= n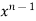 f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).( )
)
Now multiplying by x on both sides, we get
x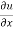 = n
= n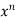 f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).( ) ---------- (2)
) ---------- (2)
Again partially differentiate equation (1) with respect to y,
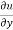 = xⁿ f’(y/x).
= xⁿ f’(y/x).
Now multiplying by y on both sides,
y 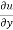 = xⁿ f’(y/x).
= xⁿ f’(y/x). ---------------(3)
---------------(3)
By adding equation (2) and (3),
x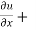 y
y 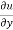 = n
= n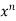 f(y/x) + + xⁿ f’(y/x).(
f(y/x) + + xⁿ f’(y/x).( ) + xⁿ f’(y/x).
) + xⁿ f’(y/x).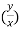
x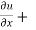 y
y 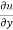 = n
= n f(y/x)
f(y/x)
Here u = f( x, y) is homogeneous function, then - u = 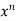 f(y/x)
f(y/x)
Put the value of u in equation (4),
x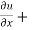 y
y 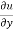 = nu
= nu
Which is the Euler’s theorem.
Q26) If u(x,y,z) = log( tan x + tan y + tan z) , then prove that ,
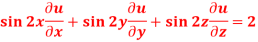
A26)
Here we have,
u(x,y,z) = log( tan x + tan y + tan z) ………………..(1)
Diff. Eq.(1) w.r.t. x , partially , we get
 ……………..(2)
……………..(2)
Diff. Eq.(1) w.r.t. y , partially , we get
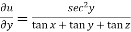 ………………(3)
………………(3)
Diff. Eq.(1) w.r.t. z , partially , we get
 ……………………(4)
……………………(4)
Now multiply eq. 2 , 3 , 4 by sin 2x , sin 2y , sin 2z respectively and adding , in order to get the final result,
We get,
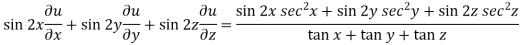

= 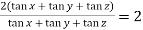
So that,
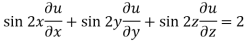
Hence proved.
Q27) Expand f(x , y) = 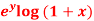 in powers of x and y about origin.
in powers of x and y about origin.
A27)
Here we have the function-
f(x , y) = 
Here , a = 0 and b = 0 then
f(0 , 0) = 
Now we will find partial derivatives of the function-
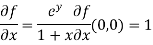


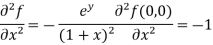
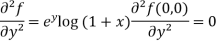
Now using Taylor’s theorem-
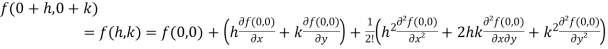 +………
+………
Suppose h = x and k = y, we get
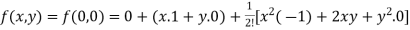 +…….
+…….
= 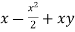 +……….
+……….
Q28) Find out the maxima and minima of the function
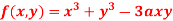
A28)
Given 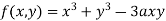 …(i)
…(i)
Partially differentiating (i) with respect to x we get
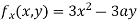 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
 ….(iii)
….(iii)
Now, form the equations 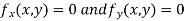
Using (ii) and (iii) we get

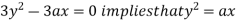
 using above two equations
using above two equations
Squaring both side we get
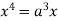
Or 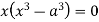
This show that 
Also we get 
Thus we get the pair of value as 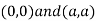
Now, we calculate
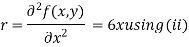
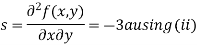
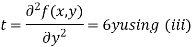
Putting above values in
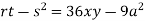
At point (0,0) we get
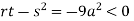
So, the point (0,0) is a saddle point.
At point 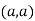 we get
we get
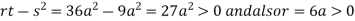
So the point 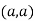 is the minimum point where
is the minimum point where 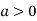
In case 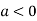
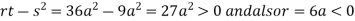
So the point 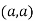 is the maximum point where
is the maximum point where 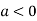
Q29) If 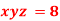 ,Find the value of x and y for which
,Find the value of x and y for which 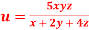 is maximum.
is maximum.
A29)
Given function is 
And relation is 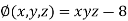
By Lagrange’s Method
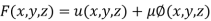
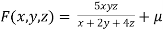 [
[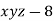 ] ..(i)
] ..(i)
Partially differentiating (i) with respect to x, y and z and equate them tozero
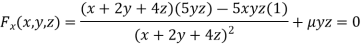
Or  …(ii)
…(ii)
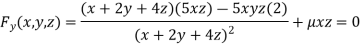
Or  …(iii)
…(iii)
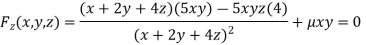
Or 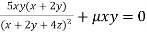 …(iv)
…(iv)
On solving (ii),(iii) and (iv) we get
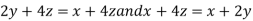
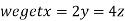
Using the given relation we get 
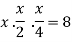
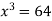
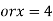
So that 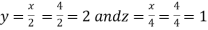
Thus the point for the maximum value of the given function is