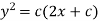Unit – 4
First order ordinary Differential Equations
Q1) What do you understand by exact differential equations?
A1)
An exact differential equation is formed by differentiating its solution directly without any other process,
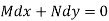
Is called an exact differential equation if it satisfies the following condition-
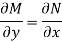
Here 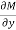 is the differential co-efficient of M with respect to y keeping x constant and
is the differential co-efficient of M with respect to y keeping x constant and  is the differential co-efficient of N with respect to x keeping y constant.
is the differential co-efficient of N with respect to x keeping y constant.
Q2) Solve  .
.
A2)
Here M =  and N =
and N = 
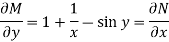
Then the equation is exact and its solution is-
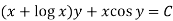
Q3) Solve-

A3)
We can write the equation as below-
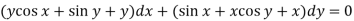
Here M = 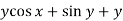 and N =
and N = 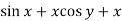
So that-

The equation is exact and its solution will be-
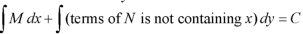

Or
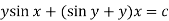
Q4) Solve (5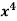 + 3
+ 3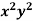 – 2x
– 2x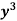 ) dx + (2
) dx + (2 y – 3
y – 3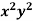 – 5
– 5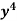 ) dy = 0
) dy = 0
A4)
Here, M = 5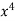 + 3
+ 3 – 2x
– 2x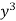 , N = 2
, N = 2 y – 3
y – 3 – 5
– 5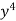
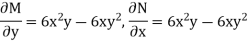
Since,  the given equation is exact.
the given equation is exact.
Now 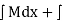 (terms
(terms  is not containing
is not containing  )
) 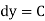 (y constant)
(y constant)
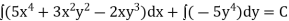
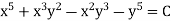
Q5) Solve
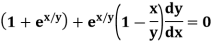
A5)
We 
 )
) 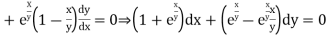
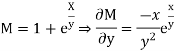

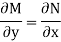
Given equation is exact.
Its solution is  (terms
(terms  not containing
not containing  )
) 
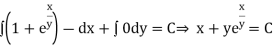
Q6) Solve) 
A6)
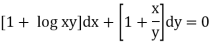
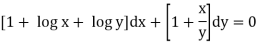
Which is in the form 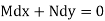
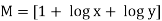 and
and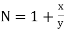
 and
and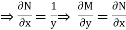
Hence the given differential equation is exact.
Solution is  (terms not containing x)
(terms not containing x) 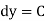
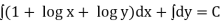
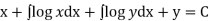 ... (1)
... (1)
Now, 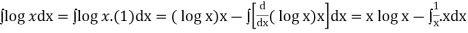
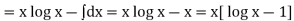
Equation (1) becomes 
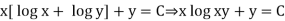
Q7) Solve-
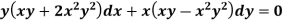
A7)
Here we have-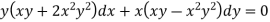
Now divide by xy, we get-

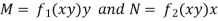
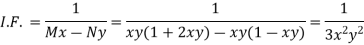
Multiply (1) by  , we get-
, we get-
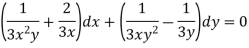
Which is an exact differential equation-
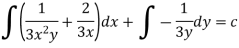
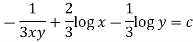
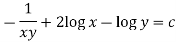
Q8) Solve-

A8)
Here given,
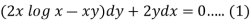
M = 2y and N = 2x log x - xy
Then-
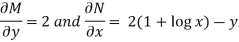
Here,
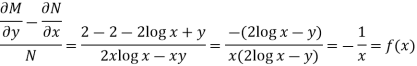
Then,
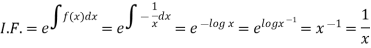
Now multiplying equation (1) by 1/x, we get-

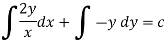
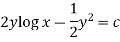
Q9) Solve 
A9)
Dividing throughout by (x+1),given equation becomes
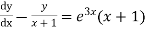 which is Leibnitz’s equation
which is Leibnitz’s equation
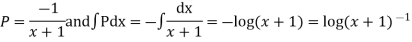
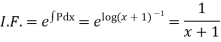
Thus the solution of (1) is 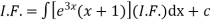
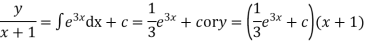
Q10) Solve 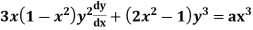
A10)
Putting 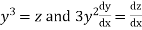 the given equation becomes
the given equation becomes
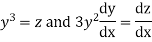
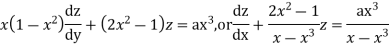
Which is Leibnitz’s equation in z.



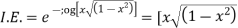
Thus the solution of (1) is
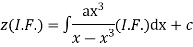
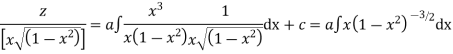
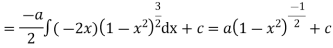
Hence the solution of the given equation is

Q11) Solve 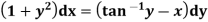
A11)
This equation contains 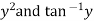 and is therefore not a linear in y, but since only z occurs, it can be written as
and is therefore not a linear in y, but since only z occurs, it can be written as
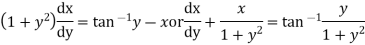
Which is a Leibnitz’s equation in z.
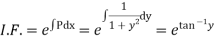
Thus the solution is 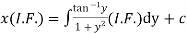
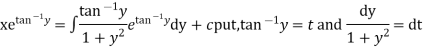
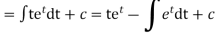
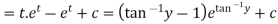
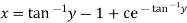
Q12) Solve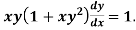
A12)
We can write the equation as-
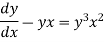
On dividing by 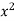 , we get-
, we get-
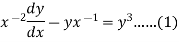
Put 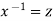 so that
so that 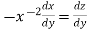
Equation (1) becomes,
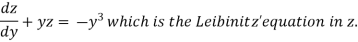
Here,

Therefore the solution is-
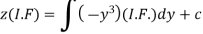
Or
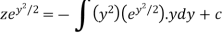
Now put 

Integrate by parts-
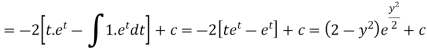
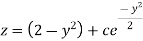
Or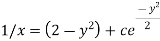
Q13) Solve 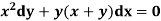
A13)
We have, 
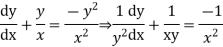
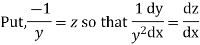
The given equation reduces to a linear differential equation in z.
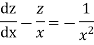
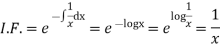
Hence the solution is
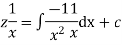
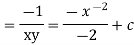
Q14) Solve 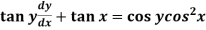
A14)
Here given,
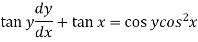
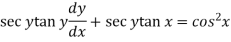
Now let z = sec y, so that dz/dx = sec y tan y dy/dx
Then the equation becomes-
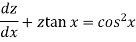
Here,
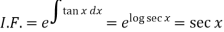
Then the solution will be-
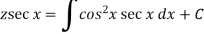
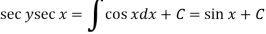
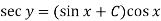
Q15) Use Euler’s method to find y(0.4) from the differential equation
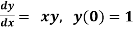 with h=0.1
with h=0.1
A15)
Given equation 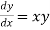
Here 
We break the interval in four steps.
So that 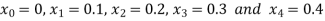
By Euler’s formula
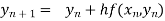 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
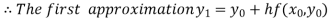

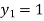
For n=1 in equation (i) we get
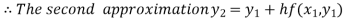

 .01
.01
For n=2 in equation (i) we get
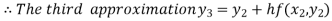
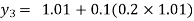
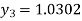
For n=3 in equation (i) we get
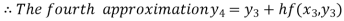
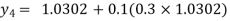
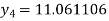
Hence y(0.4) =1.061106.
Q16) Given 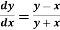 with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
A16)
Given equation is 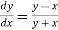
Here 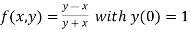
No. Of steps n=5 and so that 
So that 
Also 
By Euler’s formula
 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
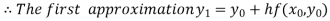
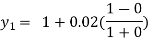

For n=1 in equation (i) we get
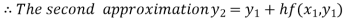


For n=2 in equation (i) we get

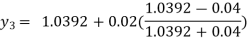

For n=3 in equation (i) we get

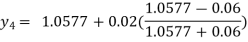

For n=4 in equation (i) we get
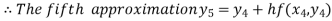
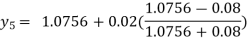
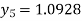
Hence 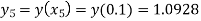
Q17) Use modified Euler’s method to compute y for x=0.05. Given that

Result correct to three decimal places.
A17)
Given equation 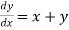
Here 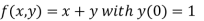
Take h = 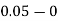 = 0.05
= 0.05
By modified Euler’s formula the initial iteration is
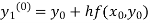
 )
)
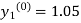
The iteration formula by modified Euler’s method is
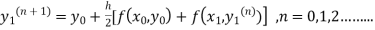 -----(i)
-----(i)
For n=0 in equation (i) we get
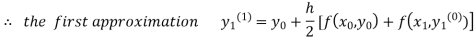
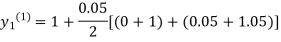
Where 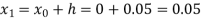 and
and 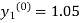 as above
as above
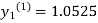
For n=1 in equation (i) we get
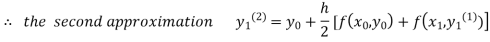
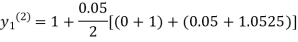
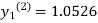
For n=3 in equation (i) we get
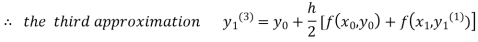
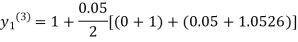
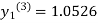
Since third and fourth approximation are equal .
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Q18) Solve 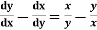
A18)
Given equation is  where
where 
Factorizing, 
Thus we have 
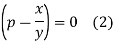
From (1) 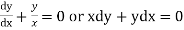
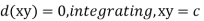
From (2) 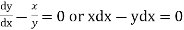
Integrating, 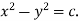 Thus x y=c or
Thus x y=c or  , constitute the required solution.
, constitute the required solution.
Otherwise combining these into one, the required solution can be written as
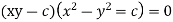
Q19) Solve 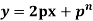
A19)
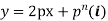
Differentiating it with respect to x we get
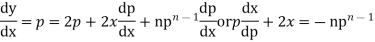
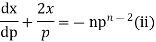
This is Leibnitz’s linear equation in x and p. Here 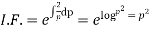
Therefore the solution of (ii) is

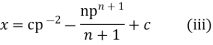
Substituting this value of x in (i) we get 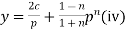
The equations (iii) and (iv) taken together with parameter p constitute the general solution (i).
Q20) Solve 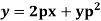
A20)

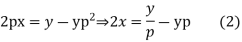
Differentiating (2) with respect to x we get

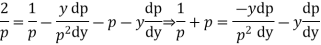
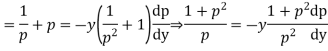
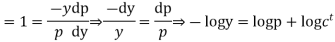
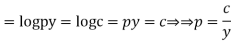
Putting the value of p in (1)