Unit - 1
Multivariable Integral Calculus
Q1) Evaluate  , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
A1)
Let, I = 
= 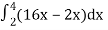
= 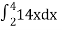
= 
= 84 sq. Unit.
Which is the required area.
Q2) Evaluate 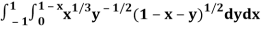
A2)
Let us suppose the integral is I,
I = 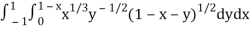
Put c = 1 – x in I, we get
I = 
Suppose, y = ct
Then dy = c
Now we get,
I = 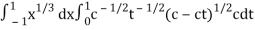
I = 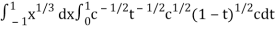
I = 
I = 
I =
As we know that by beta function,

Which gives,


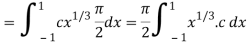
Now put the value of c, we get

= π/2 [ ¾ (1) – 3/7 (1) – ¾ (-1) + 3/7 (-1)] = π/2 [9/14] = 9π/28
Q3) Evaluate the following double integral

A3)
Let,
I = 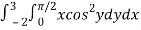
On solving the integral, we get
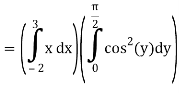
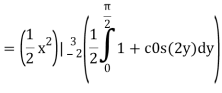
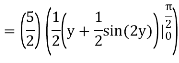
= 5π/8
Q4) Evaluate the following by changing to polar coordinates,
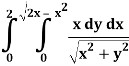
A4)
In this problem, the limits for y are 0 to  and the limits for are 0 to 2.
and the limits for are 0 to 2.
Suppose,
y = 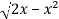
Squaring both sides,
y² = 2x - x²
x² + y² = 2x
But in polar coordinates,
We have,
r² = 2r cos θ
r = 2 cos θ
From the region of integration, r lies from 0 to 2 cos θ and θ varies from 0 to π / 2.
As we know in case of polar coordinates,
Replace x by r cos θ and y by r sin θ, dy dx by r dr dθ,
We get,
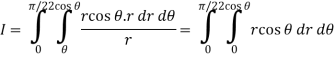
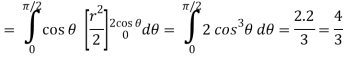
Q5) Evaluate the following integral by converting into polar coordinates.

A5)
Here limits of y,
y = 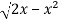
y² = 2x - x²
x² + y² = 2x
x² + y² - 2x = 0 ……………… (1)
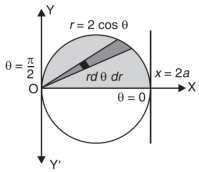
Eq. (1) represent a circle whose radius is 1 and centre is (1, 0)
Lower limit of y is zero.
Region of integration in upper half circle,
First, we will convert into polar coordinates,
By putting
x by r cos θ and y by r sin θ, dy dx by r dr dθ,
Limits of r are0 to 2 cos θ and limits of θ are from 0 to π / 2.
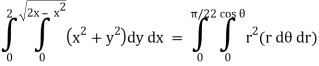

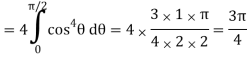
Q6) Evaluate 
A6)
Let the integral,
I = 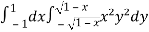
=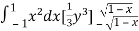
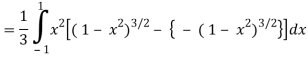



Put x = sin θ
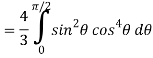
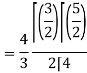
= π / 24 ans.
Q7) What is Triple integral?
A7)
Definition: Let f (x, y, z) be a function which is continuous at every point of the finite region (Volume V) of three-dimensional space. Divide the region V into n sub regions of respective volumes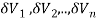 . Let (
. Let (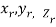 ) be a point in the
) be a point in the 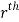 sub region then the sum:
sub region then the sum:
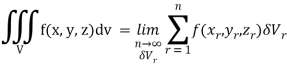
Is called triple integration of f (x, y, z) over the region V provided limit on R.H.S of above Equation exists.
Q8) Evaluate
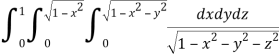
A8)
Let
I = 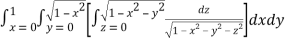
= 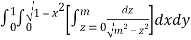
(Assuming m = 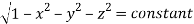 )
)
= 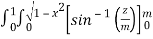 dxdy
dxdy
= 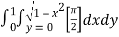
=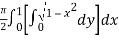
= 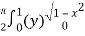 dx
dx
=  dx
dx
= 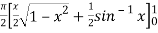
=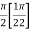
I =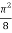
Q9) Evaluate 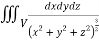 Where V is annulus between the spheres
Where V is annulus between the spheres 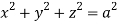 and
and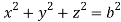 (
(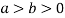 )
)
A9)
It is convenient to transform the triple integral into spherical polar co-ordinate by putting
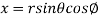 ,
, 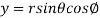 ,
, 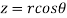
 , dxdydz=
, dxdydz=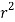 sin
sin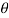 drd
drd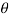 d
d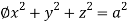 ,
,
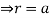 and
and

For the positive octant, r varies from r =b to r =a, 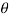 varies from
varies from 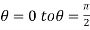
And varies from
varies from 
I= 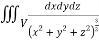
= 8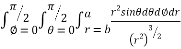
=8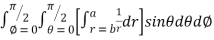
=8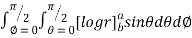
=8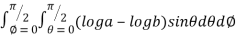
=8 log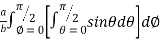
= 8 log
I= 8 log I = 4 log
I = 4 log
Q10) Evaluate 
A10)

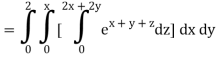

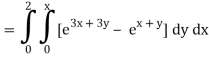

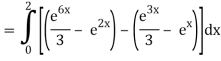
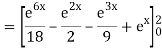
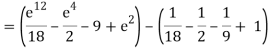
= 1/18 [e12 – 2e6 – 9e4 + 18e2 – 8]
Q11) Evaluate
 , taken through out the volume of the sphere x2 + y2 + z2 = 1 in positive octant.
, taken through out the volume of the sphere x2 + y2 + z2 = 1 in positive octant.
A11)
Put x = r sin θ sin , z = r cos θ, dx dy dz = r2 sin θ dr dθ d
θ = 0 to π/2, r= 0 to 1 and x2 + y2 + z2 = r2 φ = 0 to π/2
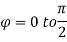

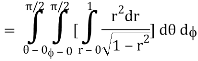

Where I1 = 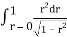 put r = sin t
put r = sin t
Dr = cos dt r 0 1
t 0 π/2
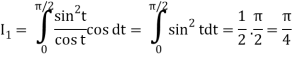
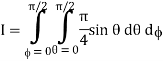
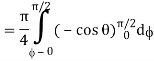
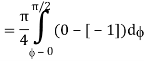
= π/4 . ()π/20
= π/4 . π/2
= π2/8
Q12) Find Volume of the tetrahedron bounded by the co-ordinate’s planes and the plane
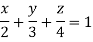
A12)
Volume =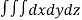 ………. (1)
………. (1)
Put  ,
, 
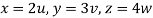
From equation (1) we have
V = 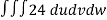
=24
=24 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 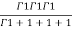
=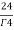 =
=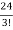 = 4
= 4
Volume =4
Q13) Find volume common to the cylinders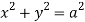 ,
,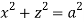 .
.
A13)
For given cylinders,
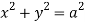 ,
, 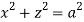 .
.
Z varies from
Z=- to z =
to z = 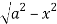
Y varies from
y= -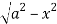 to y =
to y = 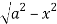
x varies from x= -a to x = a
By symmetry,
Required volume= 8 (volume in the first octant)
=8 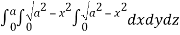
=8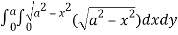
= 8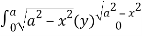 dx
dx
=8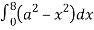
=8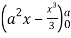
=8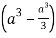
Volume = 16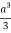
Q14) Evaluate
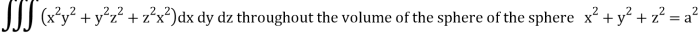
A14)
Put x = r sin θ cos , y = r sin θ sin , z = r cos θ
θ = 0 to π, = 0 to 2π, r = 0 to 1, dx dy dz = r2 sin θ dr dθ d
I = 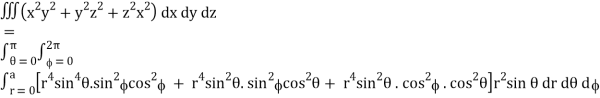
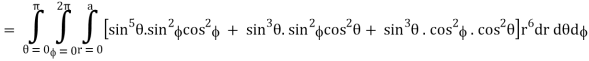
= 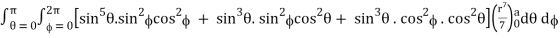
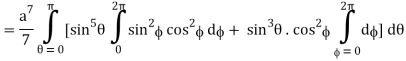
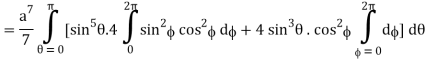


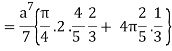
= 4a7π / 35
Q15) Integrate  through out the volume bounded x = 0, y=0, z = 0, x/a + y/b+z/c = 1.
through out the volume bounded x = 0, y=0, z = 0, x/a + y/b+z/c = 1.
A15)
x = au dx = a du
y = bv dy = b dv
z = cw dz = c dw
I = 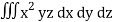
= 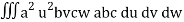
= a3 b2 c2 
= a3b2c2 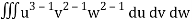
= a3b2c2 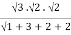
= a3b2c2 2!/7!
= a3b2c2/2520
Q16) Evaluate 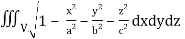 throught the volume of the ellipsoid
throught the volume of the ellipsoid 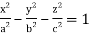
A16)
Put
x = ar sin θ cos
y = br sin θ sin
z = cr cos θ
Dxdydz = abc r2 drdθd
θ = 0 to π, = 0 to 2π, r = 0 to 1
I = 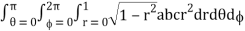
= abc 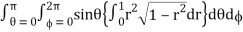
Put r = sin t dr = cos t dt
If r = 0 then t = 0 and r = 1 then t = π/2
Abc 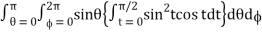
= abc 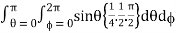
= abcπ/16 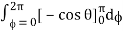
= abcπ/16 
= abcπ/8 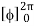
= abcπ2/4
Q17) Evaluate

By changing the order of integration.
A17)
The given limits are (inner) y from x to π/2; (Outer) x from 0 to π/2.
We use these to sketch the region of integration.
The given limits have inner variable y. To reverse the order of integration we use horizontal stripes. The limits in this order are
(inner) x from 0 to y; (outer) y from 0 to π/2.
So the integral becomes
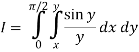
We compute the inner, then the outer integrals.
Inner: 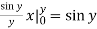 Outer: - cos
Outer: - cos  =1
=1
Q18) Change the order of integration in 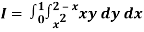 Of hence evaluate the same.
Of hence evaluate the same.
A18)
y = x2 & y = 2 - x
Pt. Of interaction:
x2 + x + 2 = 0
x = 1, 2
y = 1
(1, 1) is coordinate for A
Region of interaction is divided into 2 parts OAM and MAB
For region OAM:
0 ≤ y ≤ 1, 0 ≤ x ≤ y
For region MAB:
1 ≤ y ≤ 2, 0 ≤ x ≤ 2 –y
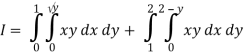
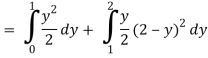
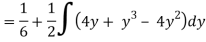
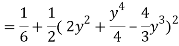
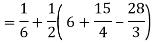
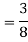
Q19) Change the order of integration of evaluate

A19)
y = x2/4a & y = 2ax
x2 = 4ay & y2 = 4ax
Pt. Of intersection
x4/16a2 = 4ax
x4 – 64 a3x3 = 0
x = 0, 4a
pts, are (0, 0), (4a, 4a)
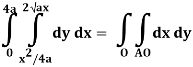
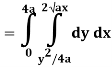
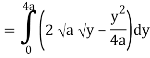
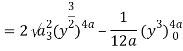
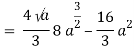
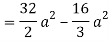

Q20) Evaluate 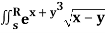 .dA
.dA
A20)
Here’s is the region bounded by the lines on the real lines
X+ y=0; x+ y=-1
x- y=0 ; x-y = 8
Let
u=x+ y , 0 u 1
v=x-y, 0 v 8
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
Solving for x and y
[ u = x+y] + [ v = x – y] = u + v = 2x
[ u = x+y ] – [ v = x – y] = u – v = 2y
X=1/2(u)+1/2(v) and y =1/2(u-1/2(v)
Using of inverse method:
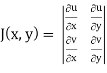 and J(x, y) . J(u, v) = 1
and J(x, y) . J(u, v) = 1
J(u, v) = 1/J(u, v)
J(u, v) = 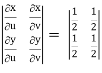
J(u, v) = (- ¼ ) – ( ¼ ) = - ½

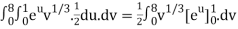
½ (e – 1) 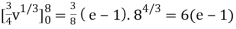
J(u, v) = 6(e – 1)
Q21) Evaluate 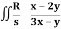 .dA
.dA
A21)
Here s is the region bounded by the lines on the real lines
X - 2y=0; x - 2y= 4
3x-y=1; 3 x-y = 8
Let
u=x – 2y
v= 3x- y
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
Using of inverse method:
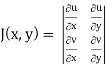 and J(x, y) . J(u, v) = 1
and J(x, y) . J(u, v) = 1
J(u, v) = 1/J(u, v)
J(u, v) = 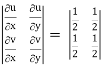
where u/x = 1, u/y = - 2, v/x = 3, v/x = - 1
J(x, y) = 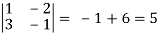
J(u, v) = 1/J(x, y) J(u, v) = 1/5
Q22) Given a plane z= 3x+4y+2 that lies above the rectangle [0,5] [1,4]. Find the surface area
A22)
The area of the surface with equation z=f(x,y),(x,y)∈ D ,where fx and fy are continuous,
Is A(S)=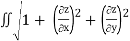 dA
dA
We have z=2+3x+4y.
Then, z/x = 3 and z/y = 4
A(S) = 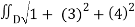 dA
dA
From the dimensions of the rectangle, we get the limits of x as (0,5) and the limits of y as(1,4)
On substituting the known values in the expression for area ,we get
A(S) = 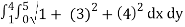
Evaluate the iterated integral.
A(S) =
= 
=15 26
Q23) Evaluate the following:
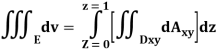
A23)
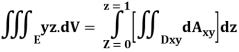


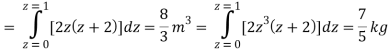
Q24) Evaluate the following:
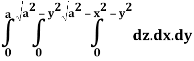
A24)
Let I = 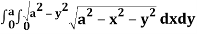
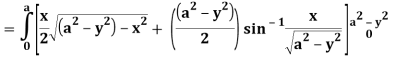
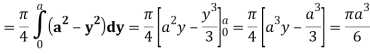
Q25) Evaluate the following triple integral

A25)
Let 
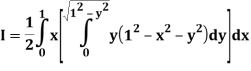
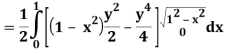

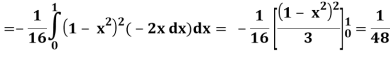
Q26) Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
A26)
Let,
y = 2 – x ………………. (1)
And y² = 2 (2 – x) ………………. (2)
On solving eq. (1) and (2)
We get the intersection points (2,0) and (0,2),
We know that,
Area = 
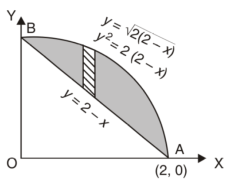
Here we will find the area as below,
Area = 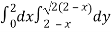
= 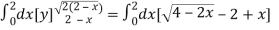
= 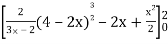
= 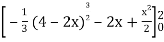
Which gives,
= (- 4 + 4 /2) + 8 / 3 = 2 / 3.
Q27) Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.
A27)
We know that,
Volume = 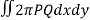
Here , PQ = 3 – x,
= 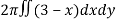
= 2π 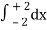
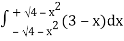
= 2π 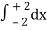 (3y – xy)+4-x2-4-x2
(3y – xy)+4-x2-4-x2
= 2π 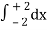 [34-x2 - x4-x2 + 34-x2 - x4-x2]
[34-x2 - x4-x2 + 34-x2 - x4-x2]
= 4π[3 4 – x2 - x4 – x2] dx = 4π [ 3 x/2 4-x2 + 3 4/2 sin-1 x/2 + 1/3(4 – x2)3/2]2-2
= 4π[ 6 π/2+ 6π/2] = 24π2
The volume is 24π².
Unit - 1
Multivariable Integral Calculus
Q1) Evaluate  , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
A1)
Let, I = 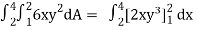
= 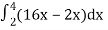
= 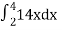
= 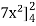
= 84 sq. Unit.
Which is the required area.
Q2) Evaluate 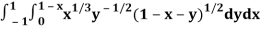
A2)
Let us suppose the integral is I,
I = 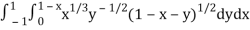
Put c = 1 – x in I, we get
I = 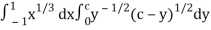
Suppose, y = ct
Then dy = c
Now we get,
I = 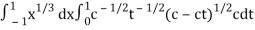
I = 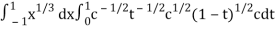
I = 
I = 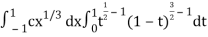
I =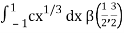
As we know that by beta function,
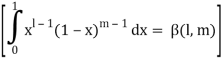
Which gives,
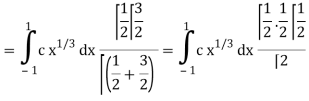
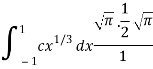
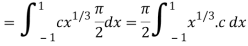
Now put the value of c, we get
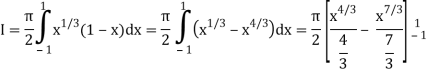
= π/2 [ ¾ (1) – 3/7 (1) – ¾ (-1) + 3/7 (-1)] = π/2 [9/14] = 9π/28
Q3) Evaluate the following double integral
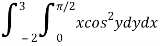
A3)
Let,
I = 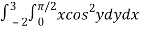
On solving the integral, we get

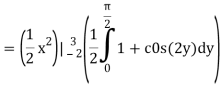
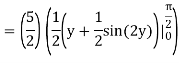
= 5π/8
Q4) Evaluate the following by changing to polar coordinates,
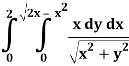
A4)
In this problem, the limits for y are 0 to  and the limits for are 0 to 2.
and the limits for are 0 to 2.
Suppose,
y = 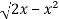
Squaring both sides,
y² = 2x - x²
x² + y² = 2x
But in polar coordinates,
We have,
r² = 2r cos θ
r = 2 cos θ
From the region of integration, r lies from 0 to 2 cos θ and θ varies from 0 to π / 2.
As we know in case of polar coordinates,
Replace x by r cos θ and y by r sin θ, dy dx by r dr dθ,
We get,
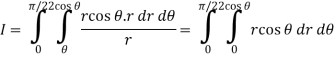
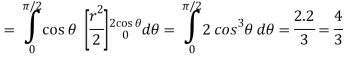
Q5) Evaluate the following integral by converting into polar coordinates.
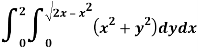
A5)
Here limits of y,
y = 
y² = 2x - x²
x² + y² = 2x
x² + y² - 2x = 0 ……………… (1)
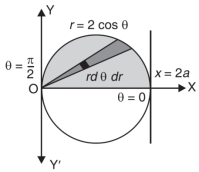
Eq. (1) represent a circle whose radius is 1 and centre is (1, 0)
Lower limit of y is zero.
Region of integration in upper half circle,
First, we will convert into polar coordinates,
By putting
x by r cos θ and y by r sin θ, dy dx by r dr dθ,
Limits of r are0 to 2 cos θ and limits of θ are from 0 to π / 2.
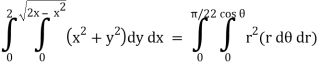
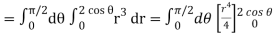
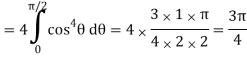
Q6) Evaluate 
A6)
Let the integral,
I = 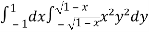
=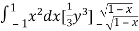
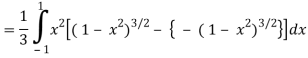
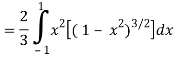
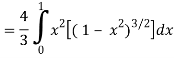

Put x = sin θ
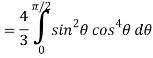
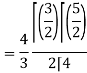
= π / 24 ans.
Q7) What is Triple integral?
A7)
Definition: Let f (x, y, z) be a function which is continuous at every point of the finite region (Volume V) of three-dimensional space. Divide the region V into n sub regions of respective volumes . Let (
. Let ( ) be a point in the
) be a point in the 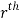 sub region then the sum:
sub region then the sum:
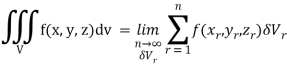
Is called triple integration of f (x, y, z) over the region V provided limit on R.H.S of above Equation exists.
Q8) Evaluate
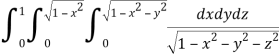
A8)
Let
I = 
= 
(Assuming m = 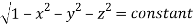 )
)
= 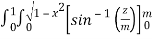 dxdy
dxdy
= 
=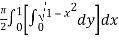
=  dx
dx
= 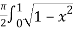 dx
dx
= 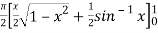
=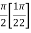
I =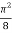
Q9) Evaluate 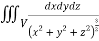 Where V is annulus between the spheres
Where V is annulus between the spheres  and
and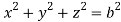 (
(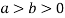 )
)
A9)
It is convenient to transform the triple integral into spherical polar co-ordinate by putting
 ,
, 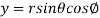 ,
, 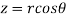
 , dxdydz=
, dxdydz= sin
sin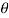 drd
drd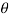 d
d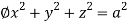 ,
,
 and
and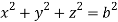
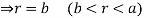
For the positive octant, r varies from r =b to r =a, 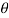 varies from
varies from 
And varies from
varies from 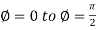
I= 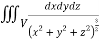
= 8
=8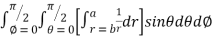
=8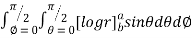
=8
=8 log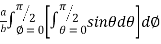
= 8 log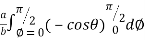
I= 8 log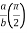 I = 4 log
I = 4 log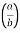
Q10) Evaluate 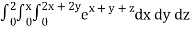
A10)

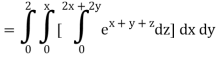
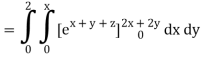


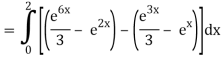
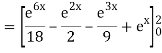
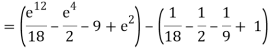
= 1/18 [e12 – 2e6 – 9e4 + 18e2 – 8]
Q11) Evaluate
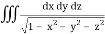 , taken through out the volume of the sphere x2 + y2 + z2 = 1 in positive octant.
, taken through out the volume of the sphere x2 + y2 + z2 = 1 in positive octant.
A11)
Put x = r sin θ sin , z = r cos θ, dx dy dz = r2 sin θ dr dθ d
θ = 0 to π/2, r= 0 to 1 and x2 + y2 + z2 = r2 φ = 0 to π/2
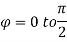


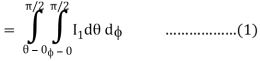
Where I1 = 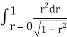 put r = sin t
put r = sin t
Dr = cos dt r 0 1
t 0 π/2

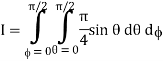
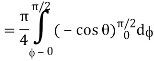

= π/4 . ()π/20
= π/4 . π/2
= π2/8
Q12) Find Volume of the tetrahedron bounded by the co-ordinate’s planes and the plane
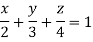
A12)
Volume =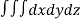 ………. (1)
………. (1)
Put 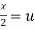 ,
, 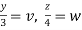
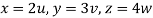
From equation (1) we have
V = 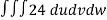
=24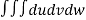
=24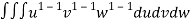 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 
=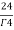 =
= = 4
= 4
Volume =4
Q13) Find volume common to the cylinders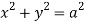 ,
,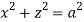 .
.
A13)
For given cylinders,
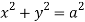 ,
, 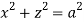 .
.
Z varies from
Z=- to z =
to z = 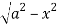
Y varies from
y= -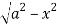 to y =
to y = 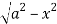
x varies from x= -a to x = a
By symmetry,
Required volume= 8 (volume in the first octant)
=8 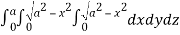
=8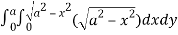
= 8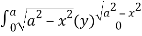 dx
dx
=8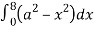
=8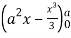
=8
Volume = 16
Q14) Evaluate
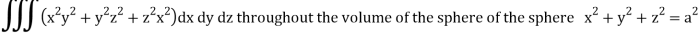
A14)
Put x = r sin θ cos , y = r sin θ sin , z = r cos θ
θ = 0 to π, = 0 to 2π, r = 0 to 1, dx dy dz = r2 sin θ dr dθ d
I = 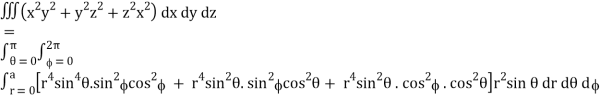
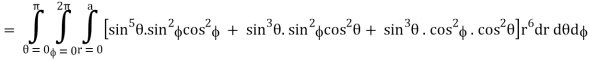
= 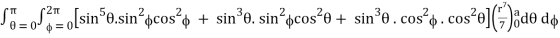

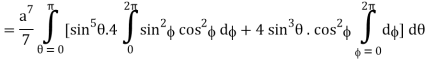
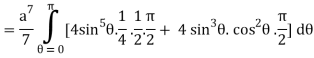

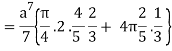
= 4a7π / 35
Q15) Integrate 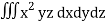 through out the volume bounded x = 0, y=0, z = 0, x/a + y/b+z/c = 1.
through out the volume bounded x = 0, y=0, z = 0, x/a + y/b+z/c = 1.
A15)
x = au dx = a du
y = bv dy = b dv
z = cw dz = c dw
I = 
= 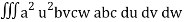
= a3 b2 c2 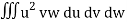
= a3b2c2 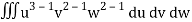
= a3b2c2 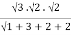
= a3b2c2 2!/7!
= a3b2c2/2520
Q16) Evaluate 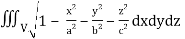 throught the volume of the ellipsoid
throught the volume of the ellipsoid 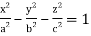
A16)
Put
x = ar sin θ cos
y = br sin θ sin
z = cr cos θ
Dxdydz = abc r2 drdθd
θ = 0 to π, = 0 to 2π, r = 0 to 1
I = 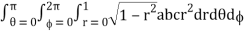
= abc 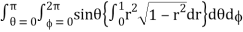
Put r = sin t dr = cos t dt
If r = 0 then t = 0 and r = 1 then t = π/2
Abc 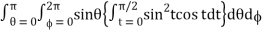
= abc 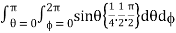
= abcπ/16 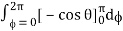
= abcπ/16 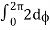
= abcπ/8 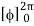
= abcπ2/4
Q17) Evaluate
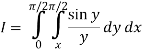
By changing the order of integration.
A17)
The given limits are (inner) y from x to π/2; (Outer) x from 0 to π/2.
We use these to sketch the region of integration.
The given limits have inner variable y. To reverse the order of integration we use horizontal stripes. The limits in this order are
(inner) x from 0 to y; (outer) y from 0 to π/2.
So the integral becomes
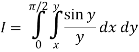
We compute the inner, then the outer integrals.
Inner: 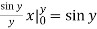 Outer: - cos
Outer: - cos  =1
=1
Q18) Change the order of integration in 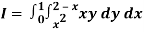 Of hence evaluate the same.
Of hence evaluate the same.
A18)
y = x2 & y = 2 - x
Pt. Of interaction:
x2 + x + 2 = 0
x = 1, 2
y = 1
(1, 1) is coordinate for A
Region of interaction is divided into 2 parts OAM and MAB
For region OAM:
0 ≤ y ≤ 1, 0 ≤ x ≤ y
For region MAB:
1 ≤ y ≤ 2, 0 ≤ x ≤ 2 –y
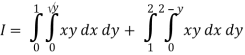
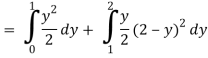
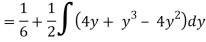
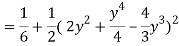


Q19) Change the order of integration of evaluate

A19)
y = x2/4a & y = 2ax
x2 = 4ay & y2 = 4ax
Pt. Of intersection
x4/16a2 = 4ax
x4 – 64 a3x3 = 0
x = 0, 4a
pts, are (0, 0), (4a, 4a)


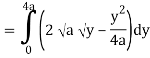
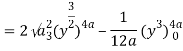
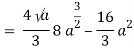
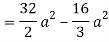

Q20) Evaluate 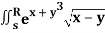 .dA
.dA
A20)
Here’s is the region bounded by the lines on the real lines
X+ y=0; x+ y=-1
x- y=0 ; x-y = 8
Let
u=x+ y , 0 u 1
v=x-y, 0 v 8
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
Solving for x and y
[ u = x+y] + [ v = x – y] = u + v = 2x
[ u = x+y ] – [ v = x – y] = u – v = 2y
X=1/2(u)+1/2(v) and y =1/2(u-1/2(v)
Using of inverse method:
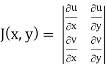 and J(x, y) . J(u, v) = 1
and J(x, y) . J(u, v) = 1
J(u, v) = 1/J(u, v)
J(u, v) = 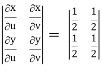
J(u, v) = (- ¼ ) – ( ¼ ) = - ½


½ (e – 1) 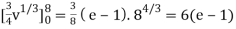
J(u, v) = 6(e – 1)
Q21) Evaluate 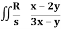 .dA
.dA
A21)
Here s is the region bounded by the lines on the real lines
X - 2y=0; x - 2y= 4
3x-y=1; 3 x-y = 8
Let
u=x – 2y
v= 3x- y
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
Using of inverse method:
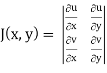 and J(x, y) . J(u, v) = 1
and J(x, y) . J(u, v) = 1
J(u, v) = 1/J(u, v)
J(u, v) = 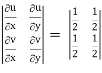
where u/x = 1, u/y = - 2, v/x = 3, v/x = - 1
J(x, y) = 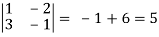
J(u, v) = 1/J(x, y) J(u, v) = 1/5
Q22) Given a plane z= 3x+4y+2 that lies above the rectangle [0,5] [1,4]. Find the surface area
A22)
The area of the surface with equation z=f(x,y),(x,y)∈ D ,where fx and fy are continuous,
Is A(S)=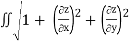 dA
dA
We have z=2+3x+4y.
Then, z/x = 3 and z/y = 4
A(S) =  dA
dA
From the dimensions of the rectangle, we get the limits of x as (0,5) and the limits of y as(1,4)
On substituting the known values in the expression for area ,we get
A(S) = 
Evaluate the iterated integral.
A(S) =
= 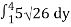
=15 26
Q23) Evaluate the following:
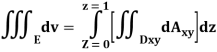
A23)



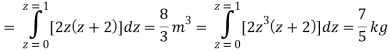
Q24) Evaluate the following:

A24)
Let I = 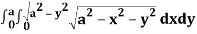
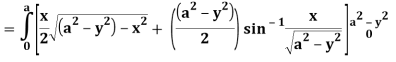
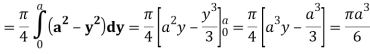
Q25) Evaluate the following triple integral

A25)
Let 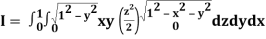
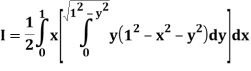
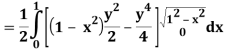

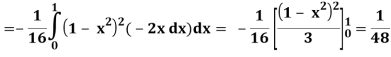
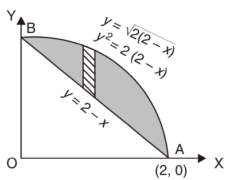
Q26) Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
A26)
Let,
y = 2 – x ………………. (1)
And y² = 2 (2 – x) ………………. (2)
On solving eq. (1) and (2)
We get the intersection points (2,0) and (0,2),
We know that,
Area = 
Here we will find the area as below,
Area = 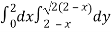
= 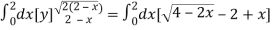
= 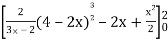
= 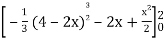
Which gives,
= (- 4 + 4 /2) + 8 / 3 = 2 / 3.
Q27) Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.
A27)
We know that,
Volume = 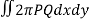
Here , PQ = 3 – x,
= 
= 2π 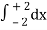

= 2π  (3y – xy)+4-x2-4-x2
(3y – xy)+4-x2-4-x2
= 2π 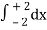 [34-x2 - x4-x2 + 34-x2 - x4-x2]
[34-x2 - x4-x2 + 34-x2 - x4-x2]
= 4π[3 4 – x2 - x4 – x2] dx = 4π [ 3 x/2 4-x2 + 3 4/2 sin-1 x/2 + 1/3(4 – x2)3/2]2-2
= 4π[ 6 π/2+ 6π/2] = 24π2
The volume is 24π².
Unit - 1
Unit - 1
Unit - 1
Unit - 1
Multivariable Integral Calculus
Q1) Evaluate 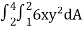 , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
A1)
Let, I = 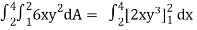
= 
= 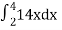
= 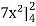
= 84 sq. Unit.
Which is the required area.
Q2) Evaluate 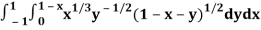
A2)
Let us suppose the integral is I,
I = 
Put c = 1 – x in I, we get
I = 
Suppose, y = ct
Then dy = c
Now we get,
I = 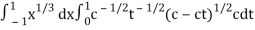
I = 
I = 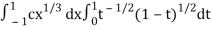
I = 
I =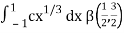
As we know that by beta function,
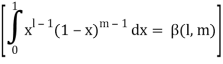
Which gives,
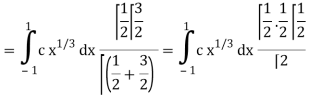

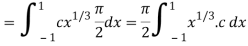
Now put the value of c, we get
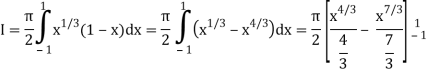
= π/2 [ ¾ (1) – 3/7 (1) – ¾ (-1) + 3/7 (-1)] = π/2 [9/14] = 9π/28
Q3) Evaluate the following double integral

A3)
Let,
I = 
On solving the integral, we get

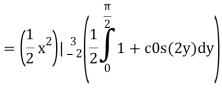
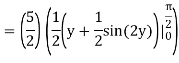
= 5π/8
Q4) Evaluate the following by changing to polar coordinates,

A4)
In this problem, the limits for y are 0 to 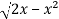 and the limits for are 0 to 2.
and the limits for are 0 to 2.
Suppose,
y = 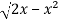
Squaring both sides,
y² = 2x - x²
x² + y² = 2x
But in polar coordinates,
We have,
r² = 2r cos θ
r = 2 cos θ
From the region of integration, r lies from 0 to 2 cos θ and θ varies from 0 to π / 2.
As we know in case of polar coordinates,
Replace x by r cos θ and y by r sin θ, dy dx by r dr dθ,
We get,
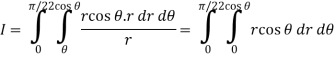

Q5) Evaluate the following integral by converting into polar coordinates.
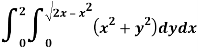
A5)
Here limits of y,
y = 
y² = 2x - x²
x² + y² = 2x
x² + y² - 2x = 0 ……………… (1)

Eq. (1) represent a circle whose radius is 1 and centre is (1, 0)
Lower limit of y is zero.
Region of integration in upper half circle,
First, we will convert into polar coordinates,
By putting
x by r cos θ and y by r sin θ, dy dx by r dr dθ,
Limits of r are0 to 2 cos θ and limits of θ are from 0 to π / 2.
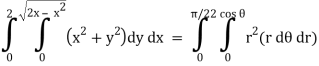
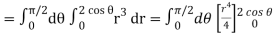
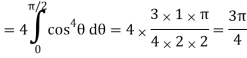
Q6) Evaluate 
A6)
Let the integral,
I = 
=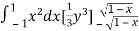

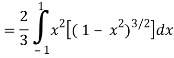

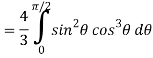
Put x = sin θ

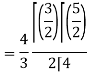
= π / 24 ans.
Q7) What is Triple integral?
A7)
Definition: Let f (x, y, z) be a function which is continuous at every point of the finite region (Volume V) of three-dimensional space. Divide the region V into n sub regions of respective volumes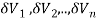 . Let (
. Let (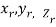 ) be a point in the
) be a point in the 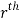 sub region then the sum:
sub region then the sum:

Is called triple integration of f (x, y, z) over the region V provided limit on R.H.S of above Equation exists.
Q8) Evaluate

A8)
Let
I = 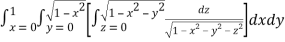
= 
(Assuming m = 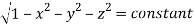 )
)
= 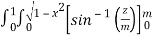 dxdy
dxdy
= 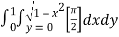
=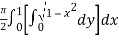
=  dx
dx
=  dx
dx
= 
=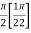
I =
Q9) Evaluate 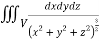 Where V is annulus between the spheres
Where V is annulus between the spheres 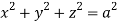 and
and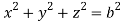 (
( )
)
A9)
It is convenient to transform the triple integral into spherical polar co-ordinate by putting
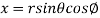 ,
,  ,
, 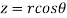
 , dxdydz=
, dxdydz=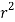 sin
sin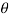 drd
drd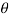 d
d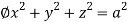 ,
,
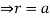 and
and
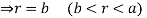
For the positive octant, r varies from r =b to r =a,  varies from
varies from 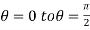
And varies from
varies from 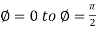
I= 
= 8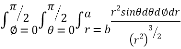
=8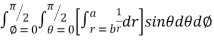
=8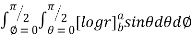
=8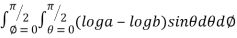
=8 log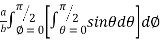
= 8 log
I= 8 log I = 4 log
I = 4 log
Q10) Evaluate 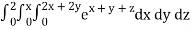
A10)

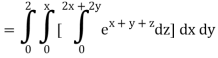
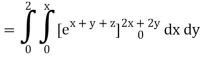
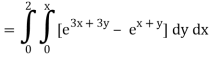
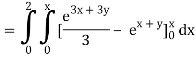

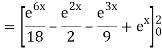
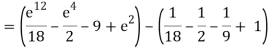
= 1/18 [e12 – 2e6 – 9e4 + 18e2 – 8]
Q11) Evaluate
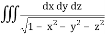 , taken through out the volume of the sphere x2 + y2 + z2 = 1 in positive octant.
, taken through out the volume of the sphere x2 + y2 + z2 = 1 in positive octant.
A11)
Put x = r sin θ sin , z = r cos θ, dx dy dz = r2 sin θ dr dθ d
θ = 0 to π/2, r= 0 to 1 and x2 + y2 + z2 = r2 φ = 0 to π/2


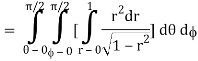
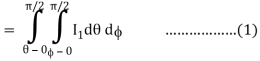
Where I1 =  put r = sin t
put r = sin t
Dr = cos dt r 0 1
t 0 π/2
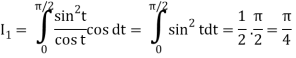
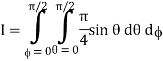

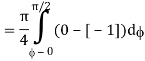
= π/4 . ()π/20
= π/4 . π/2
= π2/8
Q12) Find Volume of the tetrahedron bounded by the co-ordinate’s planes and the plane
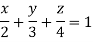
A12)
Volume = ………. (1)
………. (1)
Put 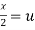 ,
, 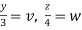
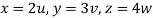
From equation (1) we have
V = 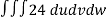
=24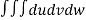
=24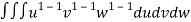 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 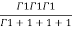
=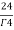 =
=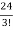 = 4
= 4
Volume =4
Q13) Find volume common to the cylinders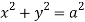 ,
, .
.
A13)
For given cylinders,
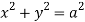 ,
, 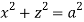 .
.
Z varies from
Z=-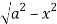 to z =
to z = 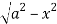
Y varies from
y= -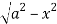 to y =
to y = 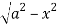
x varies from x= -a to x = a
By symmetry,
Required volume= 8 (volume in the first octant)
=8 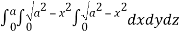
=8
= 8 dx
dx
=8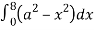
=8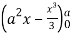
=8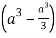
Volume = 16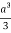
Q14) Evaluate
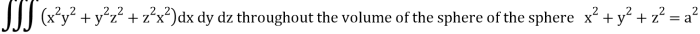
A14)
Put x = r sin θ cos , y = r sin θ sin , z = r cos θ
θ = 0 to π, = 0 to 2π, r = 0 to 1, dx dy dz = r2 sin θ dr dθ d
I = 
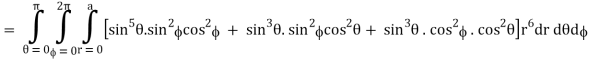
= 

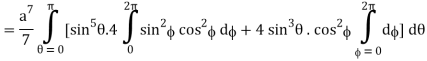
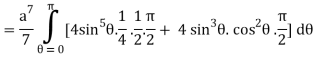


= 4a7π / 35
Q15) Integrate 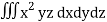 through out the volume bounded x = 0, y=0, z = 0, x/a + y/b+z/c = 1.
through out the volume bounded x = 0, y=0, z = 0, x/a + y/b+z/c = 1.
A15)
x = au dx = a du
y = bv dy = b dv
z = cw dz = c dw
I = 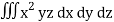
= 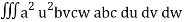
= a3 b2 c2 
= a3b2c2 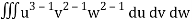
= a3b2c2 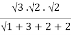
= a3b2c2 2!/7!
= a3b2c2/2520
Q16) Evaluate  throught the volume of the ellipsoid
throught the volume of the ellipsoid 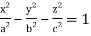
A16)
Put
x = ar sin θ cos
y = br sin θ sin
z = cr cos θ
Dxdydz = abc r2 drdθd
θ = 0 to π, = 0 to 2π, r = 0 to 1
I = 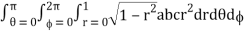
= abc 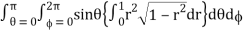
Put r = sin t dr = cos t dt
If r = 0 then t = 0 and r = 1 then t = π/2
Abc 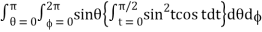
= abc 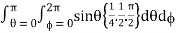
= abcπ/16 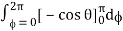
= abcπ/16 
= abcπ/8 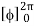
= abcπ2/4
Q17) Evaluate

By changing the order of integration.
A17)
The given limits are (inner) y from x to π/2; (Outer) x from 0 to π/2.
We use these to sketch the region of integration.
The given limits have inner variable y. To reverse the order of integration we use horizontal stripes. The limits in this order are
(inner) x from 0 to y; (outer) y from 0 to π/2.
So the integral becomes

We compute the inner, then the outer integrals.
Inner: 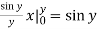 Outer: - cos
Outer: - cos 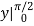 =1
=1
Q18) Change the order of integration in 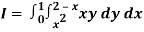 Of hence evaluate the same.
Of hence evaluate the same.
A18)
y = x2 & y = 2 - x
Pt. Of interaction:
x2 + x + 2 = 0
x = 1, 2
y = 1
(1, 1) is coordinate for A
Region of interaction is divided into 2 parts OAM and MAB
For region OAM:
0 ≤ y ≤ 1, 0 ≤ x ≤ y
For region MAB:
1 ≤ y ≤ 2, 0 ≤ x ≤ 2 –y

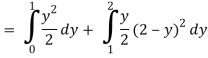

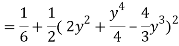
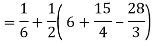

Q19) Change the order of integration of evaluate
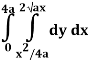
A19)
y = x2/4a & y = 2ax
x2 = 4ay & y2 = 4ax
Pt. Of intersection
x4/16a2 = 4ax
x4 – 64 a3x3 = 0
x = 0, 4a
pts, are (0, 0), (4a, 4a)

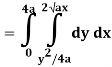
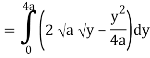
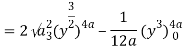

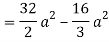

Q20) Evaluate 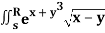 .dA
.dA
A20)
Here’s is the region bounded by the lines on the real lines
X+ y=0; x+ y=-1
x- y=0 ; x-y = 8
Let
u=x+ y , 0 u 1
v=x-y, 0 v 8
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
Solving for x and y
[ u = x+y] + [ v = x – y] = u + v = 2x
[ u = x+y ] – [ v = x – y] = u – v = 2y
X=1/2(u)+1/2(v) and y =1/2(u-1/2(v)
Using of inverse method:
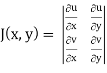 and J(x, y) . J(u, v) = 1
and J(x, y) . J(u, v) = 1
J(u, v) = 1/J(u, v)
J(u, v) = 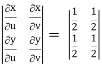
J(u, v) = (- ¼ ) – ( ¼ ) = - ½
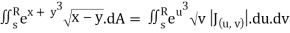
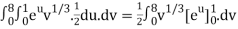
½ (e – 1) 
J(u, v) = 6(e – 1)
Q21) Evaluate 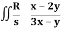 .dA
.dA
A21)
Here s is the region bounded by the lines on the real lines
X - 2y=0; x - 2y= 4
3x-y=1; 3 x-y = 8
Let
u=x – 2y
v= 3x- y
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
Using of inverse method:
 and J(x, y) . J(u, v) = 1
and J(x, y) . J(u, v) = 1
J(u, v) = 1/J(u, v)
J(u, v) = 
where u/x = 1, u/y = - 2, v/x = 3, v/x = - 1
J(x, y) = 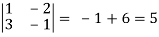
J(u, v) = 1/J(x, y) J(u, v) = 1/5
Q22) Given a plane z= 3x+4y+2 that lies above the rectangle [0,5] [1,4]. Find the surface area
A22)
The area of the surface with equation z=f(x,y),(x,y)∈ D ,where fx and fy are continuous,
Is A(S)=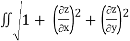 dA
dA
We have z=2+3x+4y.
Then, z/x = 3 and z/y = 4
A(S) =  dA
dA
From the dimensions of the rectangle, we get the limits of x as (0,5) and the limits of y as(1,4)
On substituting the known values in the expression for area ,we get
A(S) = 
Evaluate the iterated integral.
A(S) =
= 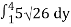
=15 26
Q23) Evaluate the following:
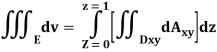
A23)


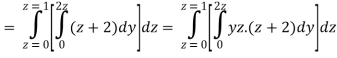
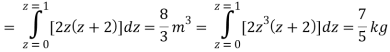
Q24) Evaluate the following:
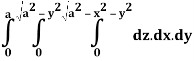
A24)
Let I = 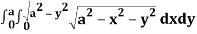
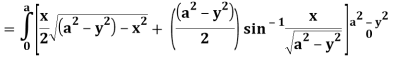
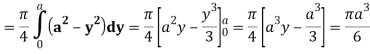
Q25) Evaluate the following triple integral
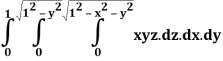
A25)
Let 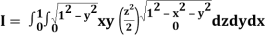
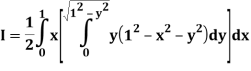
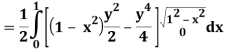
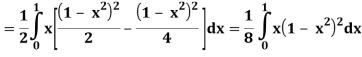
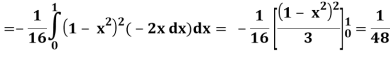
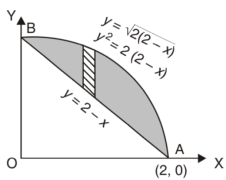
Q26) Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
A26)
Let,
y = 2 – x ………………. (1)
And y² = 2 (2 – x) ………………. (2)
On solving eq. (1) and (2)
We get the intersection points (2,0) and (0,2),
We know that,
Area = 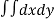
Here we will find the area as below,
Area = 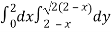
= 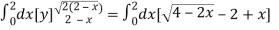
= 
= 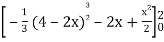
Which gives,
= (- 4 + 4 /2) + 8 / 3 = 2 / 3.
Q27) Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.
A27)
We know that,
Volume = 
Here , PQ = 3 – x,
= 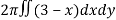
= 2π 
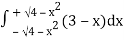
= 2π 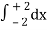 (3y – xy)+4-x2-4-x2
(3y – xy)+4-x2-4-x2
= 2π  [34-x2 - x4-x2 + 34-x2 - x4-x2]
[34-x2 - x4-x2 + 34-x2 - x4-x2]
= 4π[3 4 – x2 - x4 – x2] dx = 4π [ 3 x/2 4-x2 + 3 4/2 sin-1 x/2 + 1/3(4 – x2)3/2]2-2
= 4π[ 6 π/2+ 6π/2] = 24π2
The volume is 24π².
Unit - 1
Multivariable Integral Calculus
Q1) Evaluate 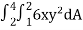 , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
A1)
Let, I = 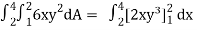
= 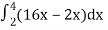
= 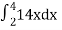
= 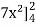
= 84 sq. Unit.
Which is the required area.
Q2) Evaluate 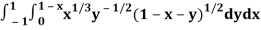
A2)
Let us suppose the integral is I,
I = 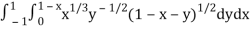
Put c = 1 – x in I, we get
I = 
Suppose, y = ct
Then dy = c
Now we get,
I = 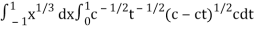
I = 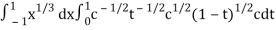
I = 
I = 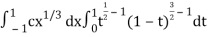
I =
As we know that by beta function,
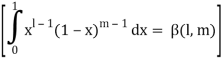
Which gives,
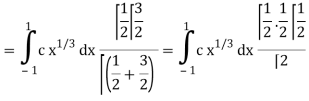

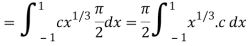
Now put the value of c, we get
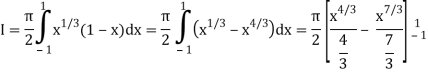
= π/2 [ ¾ (1) – 3/7 (1) – ¾ (-1) + 3/7 (-1)] = π/2 [9/14] = 9π/28
Q3) Evaluate the following double integral
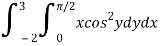
A3)
Let,
I = 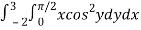
On solving the integral, we get

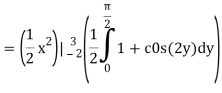
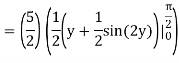
= 5π/8
Q4) Evaluate the following by changing to polar coordinates,
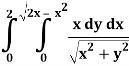
A4)
In this problem, the limits for y are 0 to  and the limits for are 0 to 2.
and the limits for are 0 to 2.
Suppose,
y = 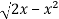
Squaring both sides,
y² = 2x - x²
x² + y² = 2x
But in polar coordinates,
We have,
r² = 2r cos θ
r = 2 cos θ
From the region of integration, r lies from 0 to 2 cos θ and θ varies from 0 to π / 2.
As we know in case of polar coordinates,
Replace x by r cos θ and y by r sin θ, dy dx by r dr dθ,
We get,
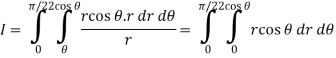
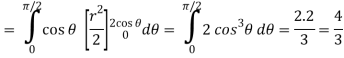
Q5) Evaluate the following integral by converting into polar coordinates.
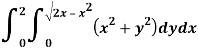
A5)
Here limits of y,
y = 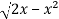
y² = 2x - x²
x² + y² = 2x
x² + y² - 2x = 0 ……………… (1)
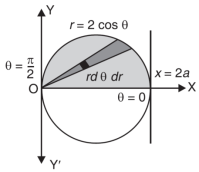
Eq. (1) represent a circle whose radius is 1 and centre is (1, 0)
Lower limit of y is zero.
Region of integration in upper half circle,
First, we will convert into polar coordinates,
By putting
x by r cos θ and y by r sin θ, dy dx by r dr dθ,
Limits of r are0 to 2 cos θ and limits of θ are from 0 to π / 2.
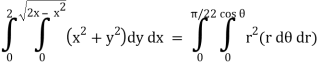
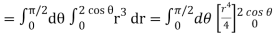
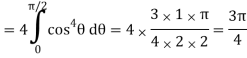
Q6) Evaluate 
A6)
Let the integral,
I = 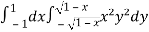
=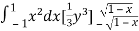
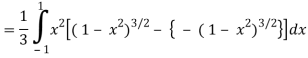

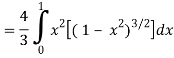
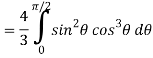
Put x = sin θ

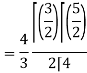
= π / 24 ans.
Q7) What is Triple integral?
A7)
Definition: Let f (x, y, z) be a function which is continuous at every point of the finite region (Volume V) of three-dimensional space. Divide the region V into n sub regions of respective volumes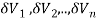 . Let (
. Let (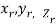 ) be a point in the
) be a point in the  sub region then the sum:
sub region then the sum:
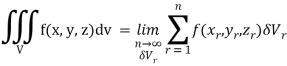
Is called triple integration of f (x, y, z) over the region V provided limit on R.H.S of above Equation exists.
Q8) Evaluate
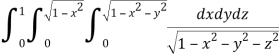
A8)
Let
I = 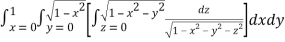
= 
(Assuming m = 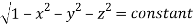 )
)
= 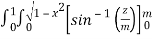 dxdy
dxdy
= 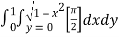
=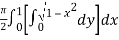
=  dx
dx
=  dx
dx
= 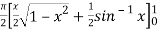
=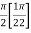
I =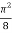
Q9) Evaluate  Where V is annulus between the spheres
Where V is annulus between the spheres 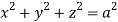 and
and (
(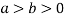 )
)
A9)
It is convenient to transform the triple integral into spherical polar co-ordinate by putting
 ,
,  ,
, 
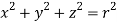 , dxdydz=
, dxdydz=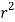 sin
sin drd
drd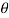 d
d ,
,
 and
and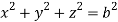
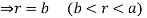
For the positive octant, r varies from r =b to r =a, 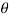 varies from
varies from 
And varies from
varies from 
I= 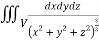
= 8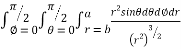
=8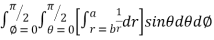
=8
=8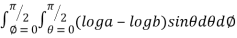
=8 log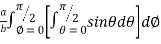
= 8 log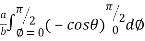
I= 8 log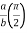 I = 4 log
I = 4 log
Q10) Evaluate 
A10)
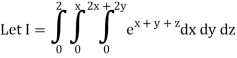
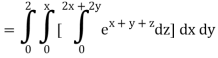
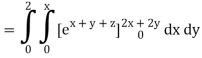

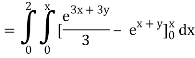
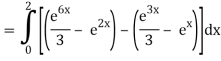
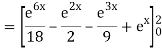
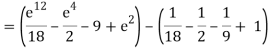
= 1/18 [e12 – 2e6 – 9e4 + 18e2 – 8]
Q11) Evaluate
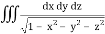 , taken through out the volume of the sphere x2 + y2 + z2 = 1 in positive octant.
, taken through out the volume of the sphere x2 + y2 + z2 = 1 in positive octant.
A11)
Put x = r sin θ sin , z = r cos θ, dx dy dz = r2 sin θ dr dθ d
θ = 0 to π/2, r= 0 to 1 and x2 + y2 + z2 = r2 φ = 0 to π/2



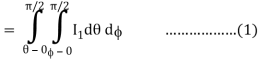
Where I1 =  put r = sin t
put r = sin t
Dr = cos dt r 0 1
t 0 π/2




= π/4 . ()π/20
= π/4 . π/2
= π2/8
Q12) Find Volume of the tetrahedron bounded by the co-ordinate’s planes and the plane
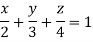
A12)
Volume =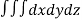 ………. (1)
………. (1)
Put 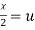 ,
, 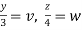
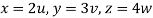
From equation (1) we have
V = 
=24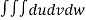
=24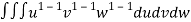 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 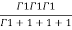
=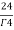 =
= = 4
= 4
Volume =4
Q13) Find volume common to the cylinders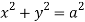 ,
,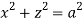 .
.
A13)
For given cylinders,
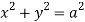 ,
,  .
.
Z varies from
Z=-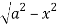 to z =
to z = 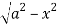
Y varies from
y= - to y =
to y = 
x varies from x= -a to x = a
By symmetry,
Required volume= 8 (volume in the first octant)
=8 
=8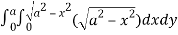
= 8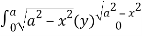 dx
dx
=8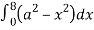
=8
=8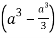
Volume = 16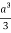
Q14) Evaluate

A14)
Put x = r sin θ cos , y = r sin θ sin , z = r cos θ
θ = 0 to π, = 0 to 2π, r = 0 to 1, dx dy dz = r2 sin θ dr dθ d
I = 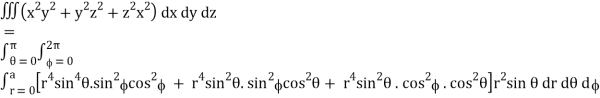

= 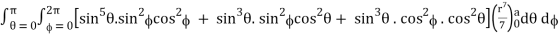
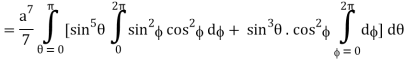
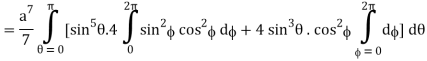
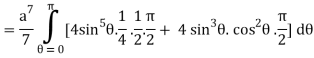
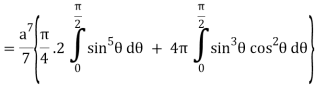
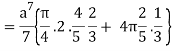
= 4a7π / 35
Q15) Integrate 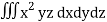 through out the volume bounded x = 0, y=0, z = 0, x/a + y/b+z/c = 1.
through out the volume bounded x = 0, y=0, z = 0, x/a + y/b+z/c = 1.
A15)
x = au dx = a du
y = bv dy = b dv
z = cw dz = c dw
I = 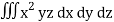
= 
= a3 b2 c2 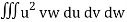
= a3b2c2 
= a3b2c2 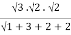
= a3b2c2 2!/7!
= a3b2c2/2520
Q16) Evaluate 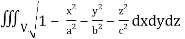 throught the volume of the ellipsoid
throught the volume of the ellipsoid 
A16)
Put
x = ar sin θ cos
y = br sin θ sin
z = cr cos θ
Dxdydz = abc r2 drdθd
θ = 0 to π, = 0 to 2π, r = 0 to 1
I = 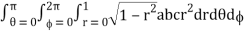
= abc 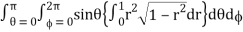
Put r = sin t dr = cos t dt
If r = 0 then t = 0 and r = 1 then t = π/2
Abc 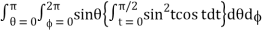
= abc 
= abcπ/16 
= abcπ/16 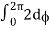
= abcπ/8 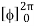
= abcπ2/4
Q17) Evaluate

By changing the order of integration.
A17)
The given limits are (inner) y from x to π/2; (Outer) x from 0 to π/2.
We use these to sketch the region of integration.
The given limits have inner variable y. To reverse the order of integration we use horizontal stripes. The limits in this order are
(inner) x from 0 to y; (outer) y from 0 to π/2.
So the integral becomes
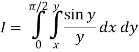
We compute the inner, then the outer integrals.
Inner: 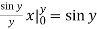 Outer: - cos
Outer: - cos  =1
=1
Q18) Change the order of integration in  Of hence evaluate the same.
Of hence evaluate the same.
A18)
y = x2 & y = 2 - x
Pt. Of interaction:
x2 + x + 2 = 0
x = 1, 2
y = 1
(1, 1) is coordinate for A
Region of interaction is divided into 2 parts OAM and MAB
For region OAM:
0 ≤ y ≤ 1, 0 ≤ x ≤ y
For region MAB:
1 ≤ y ≤ 2, 0 ≤ x ≤ 2 –y
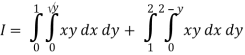

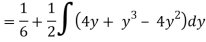
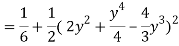
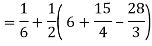

Q19) Change the order of integration of evaluate
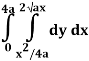
A19)
y = x2/4a & y = 2ax
x2 = 4ay & y2 = 4ax
Pt. Of intersection
x4/16a2 = 4ax
x4 – 64 a3x3 = 0
x = 0, 4a
pts, are (0, 0), (4a, 4a)
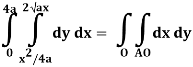



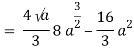


Q20) Evaluate 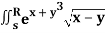 .dA
.dA
A20)
Here’s is the region bounded by the lines on the real lines
X+ y=0; x+ y=-1
x- y=0 ; x-y = 8
Let
u=x+ y , 0 u 1
v=x-y, 0 v 8
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
Solving for x and y
[ u = x+y] + [ v = x – y] = u + v = 2x
[ u = x+y ] – [ v = x – y] = u – v = 2y
X=1/2(u)+1/2(v) and y =1/2(u-1/2(v)
Using of inverse method:
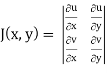 and J(x, y) . J(u, v) = 1
and J(x, y) . J(u, v) = 1
J(u, v) = 1/J(u, v)
J(u, v) = 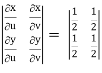
J(u, v) = (- ¼ ) – ( ¼ ) = - ½

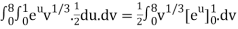
½ (e – 1) 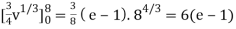
J(u, v) = 6(e – 1)
Q21) Evaluate 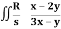 .dA
.dA
A21)
Here s is the region bounded by the lines on the real lines
X - 2y=0; x - 2y= 4
3x-y=1; 3 x-y = 8
Let
u=x – 2y
v= 3x- y
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
Using of inverse method:
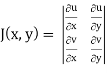 and J(x, y) . J(u, v) = 1
and J(x, y) . J(u, v) = 1
J(u, v) = 1/J(u, v)
J(u, v) = 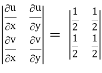
where u/x = 1, u/y = - 2, v/x = 3, v/x = - 1
J(x, y) = 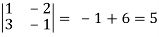
J(u, v) = 1/J(x, y) J(u, v) = 1/5
Q22) Given a plane z= 3x+4y+2 that lies above the rectangle [0,5] [1,4]. Find the surface area
A22)
The area of the surface with equation z=f(x,y),(x,y)∈ D ,where fx and fy are continuous,
Is A(S)= dA
dA
We have z=2+3x+4y.
Then, z/x = 3 and z/y = 4
A(S) = 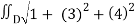 dA
dA
From the dimensions of the rectangle, we get the limits of x as (0,5) and the limits of y as(1,4)
On substituting the known values in the expression for area ,we get
A(S) = 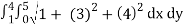
Evaluate the iterated integral.
A(S) =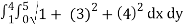
= 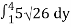
=15 26
Q23) Evaluate the following:
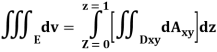
A23)

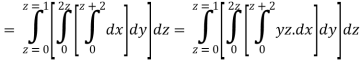
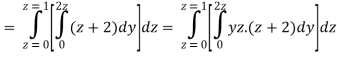
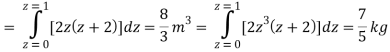
Q24) Evaluate the following:
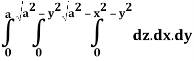
A24)
Let I = 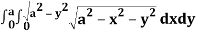
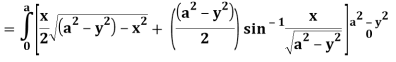

Q25) Evaluate the following triple integral
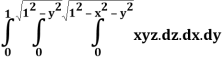
A25)
Let 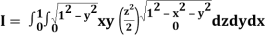
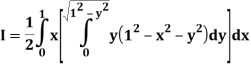
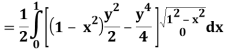

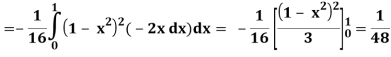
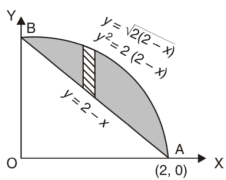
Q26) Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
A26)
Let,
y = 2 – x ………………. (1)
And y² = 2 (2 – x) ………………. (2)
On solving eq. (1) and (2)
We get the intersection points (2,0) and (0,2),
We know that,
Area = 
Here we will find the area as below,
Area = 
= 
= 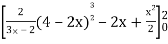
= 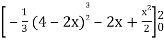
Which gives,
= (- 4 + 4 /2) + 8 / 3 = 2 / 3.
Q27) Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.
A27)
We know that,
Volume = 
Here , PQ = 3 – x,
= 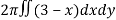
= 2π 

= 2π  (3y – xy)+4-x2-4-x2
(3y – xy)+4-x2-4-x2
= 2π 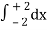 [34-x2 - x4-x2 + 34-x2 - x4-x2]
[34-x2 - x4-x2 + 34-x2 - x4-x2]
= 4π[3 4 – x2 - x4 – x2] dx = 4π [ 3 x/2 4-x2 + 3 4/2 sin-1 x/2 + 1/3(4 – x2)3/2]2-2
= 4π[ 6 π/2+ 6π/2] = 24π2
The volume is 24π².