Unit - 3

Single Phase Transformers

Q1) A 2500/200 V transformer draws a no-load primary current of 0.5 A and absorbs 400 W. Find magnetising and loss currents.

A1) Iron-loss current = No load input(W) / Primary voltage

= 400/2500 = 0.16 A

I20 = I2w + I2µ

Iµ = √I20 – I2w

= √(0.5)2 – (0.16)2

Iµ = 0.473 A

Q2) A 1-φ transformer has 1000 turns on primary and 200 on secondary. The no load current is 4 amp at p.f of 0.2 lagging. Find primary current and pf when secondary current is 280 A at pf of 0.6 lagging.

A2) cos-1 0.6 = 53.130 (sin φ = 0.8)

I2 = 280/-53.130A

Φ = cos-1 0.2 = 78.50

Sin φ = 0.98

I1 = I0 + I’2

I’2 = (I2/K) ( -53.130

K = N1/N2 = 1000/200 = 5

I’2 = 280/5 (-53.130

I’2 = 56(-53.130

I1 = I0 + I’2

= 4(0.20 – j0.98) + 56(0.6 – j0.8)

= 0.80 – j3.92 + 33.6 – j44.8

I1 = 34.4 – j48.72

I1 = 59.64 ( -54.770

I lags supply voltage by 54.770

Q3) A 1- φ transformer with ratio of 440/110-V takes a no-load current of 6 A at 0.3 pf lagging. If secondary supplies 120 A at pf of 0.8 lagging. Find current taken by primary.

A3)

Cos φ2 = 0.8

Φ2 = 36.540

Cos φ0 = 0.3

Φ0 = 72.540

K = V2/V1 = 110/440 = ¼

I’2 = KI2 = 120 x ¼ = 30 A

I0 = 6A

Angle between I0& I’2

= 72.54 – 36.54

= 35.670

From vector diagram,

I1 = √(62 + 302 + 2 x 6 x 30 cos 35.67)

I1 = 35.05 A

Q4) A – 100 KVA transformer has 500 turns on primary and 80 turns on secondary. The primary and secondary resistances are 0.3 and 0.01 Ω respectively and the corresponding leakage reactances are 1.1 and 0.035 Ω. The supply voltage is 2400 V. Find

(i). Equivalent impedance referred to primary

(ii). Voltage regulation and the secondary terminal voltage for full load having pf 0.8 lagging?

A4) Equivalent impedance referred to primary

Z01 = √R201 + X201 = R01 + jX01

R01 = R1 + R2/K2 = 0.3 + 0.01/K2 = 0.69 Ω

K = 80/500 = 4/25

X01 = X1 + X2/K2 = 1.1 + 0.035/(0.16)2 = 2.467 Ω

Z01 = 0.69 + j2.46

(ii). Secondary terminal voltage Z02 = K2 Z01

Z02 = 0.018 + j 0.063

= 0.065 ( 74.050

No-load secondary voltage = KV1

= 0.16 x 2400 = 384 V

I2 = 100 x 103/384 = 260.42 A

Full load voltage drop referred to secondary

= I2 (R02 cosφ– X02 Sinφ)

Cosφ = 0.8

Φ = 36.860

Sinφ = 0.6

= 260.42(0.018 x 0.8 – 0.063 x 0.6)

= - 6.094 V

% regn = -6.094/384 x 100

= -1.587

Secondary terminal voltage on-load

= 384 – (-6.094)

= 390.09 V

Q5) In a 50 KVA, 2200/200 V, 1-φ transformer, the iron and full-load copper  losses are 400 W and 450 W respectively. Calculate n at unity power factor on (i). Full load (ii). Half-full load?

A5)

(i). Total loss = 400 + 450 = 850 W

F.L output at unity power factor = 50 x 1

= 50 KVA

n = 50 / 50 + .850 = 50/50.850 = 0.98 = 98%

(ii). Half full load, unity pf

= 50 KVA/2 = 25 KVA

Cu loss = 400 x (1/2)2 = 100 W

Iron loss is same = 450 W

Total loss = 100 + 450 = 550 W

n = 25/25 + 0.55 = 25/25.55 = 0.978 = 97.8 %

Q6) A 40 KVA 440/220 V, 1- φ, 50 Hz transformer has iron loss of 300 W. The cu loss is found to be 100 W when delivering half full-load current. Determine (i) n when delivering full load current at 0.8 lagging pf (ii) the percentage of full-load when the efficiency will be max.

A6) Full load efficiency at 0.8 pf

= 40 x 0.8/(40 x 0.8) + losses

Full load cu loss = (440/220)2 x 100

= 400 W

Iron loss = 400 + 300

= 700 W

n = 40 x 0.8/(40 x 0.8) + 0.7 = 97.8 %

(ii). KVA for maximum / F.L KVA = √ iron loss / F.L cu loss

= √300/400 = 0.866

Q7) An auto transformer suppliers load of 4KW at 100v at unity pf. IF the applied primary voltage is 220v. Calculating power transferred to load (a) Inductively (b) conductively.

A7) Power transferred inductively = Input(1-k)

Power transferred conductively = K* Input

K= =

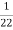
Input= Output =4KW

Inductively transferred power =4()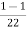

=3.82KW

Conductively transferred power =  *4

=   0.182 kw

Q8) The core of a 110 KVA, 10,000/500v, 50 Hz, 1-Φ core type transformer has a cross section of 18 cm x 18 cm. Find the number of HV and LV turns per phase and the emf per turn if the maximum core density does not exceed 1.3 tesla. Assume a stacking factor pf 0.9.

A8) Bm= 1.3T

Area = (0.18 x 0.18) = 0.032m2

Emf induced in primary

E1 = 4.44 fN1BmA

10000=4.44 x 50 x N1 x 1.3 x 0.032

N1=1082.8

Emf induced in secondary

E2 = 4.44 fN2BmA

500= 4.44 x 50 x N2 x 1.3 x 0.032

N2= 54.14

i)                   The number of turns is N1=1082.8 and N2= 54.14

Ii)                 Emf per turn = E1/E2 = N1/N2 = K

=10000/1082=9.24V or 500/54.14=9.23V

Q9) A 1-Φ transformer has 400 turns in primary and 110 turns in the secondary. The cross-sectional area of the secondary. The cross-sectional area of the core is 80cm2. If the primary winding is connected to the 50 Hz supply at 500V. Calculate peak flux density in core.

A9) As we know Emf induced in primary

E1 = 4.44 fN1BmA

500 = 4.44 x 50 x 400 x Bm x (80x10‑4)

Bm=0.704Wb/m2

Q10) A 2000/200v transformer draws a no-load primary current of 0.6A and absorbs 360 watts find the magnetising and iron loss currents.

A10) Iron loss current = = 360/2000=0.18A

I20 = I2w + I2µ

Magnetising component Iµ = √I20 – I2w

= √(0.6)2 – (0.18)2

Iµ = 0.57 A

Q11) A 2200/250 V transformer takes 0.7A at a p.f of 0.4 0n open circuit. Find the magnetising and working component of no load primary current?

A11) I0= 0.7A

Cosφ0=0.4

Iw= I0 cosφ0

Iw=0.7 x 0.4=0.28A

Magnetising component Iµ = √I20 – I2w

= √(0.7)2 – (0.280)2

Iµ = 0.64 A

Q12) A single phase transformer has 400 turns in primary and 1000 turns in secondary. The cross-sectional area is 80 cm2. If primary is connected to 50hz at 500V. Voltage induced in secondary?

A12) As we know Emf induced in primary

E1 = 4.44 fN1BmA

500= 4.44x50x1000xBmx(80x10-4)

Bm= 0.28Wb/m2

The voltage induced in secondary is given as

E1/E2 = N1/N2 = K

E2=1000x500/400=1250V

Q13) A 200 KVA, 1200/200v, 50 Hz, 1-Φ transformer has a leakage impedance of (0.1 + 0.30) Ω for the HV winding and (0.005 + 0.015) Ω for the LV winding. Find the equivalent winding resistance, reactance and impedance referred to the HV and LV side.

A13) The Turn ratio is given as E1/E2 = N1/N2 = K

K=6

i)                   Referring to High Voltage Side

Resistance = R1+K2R2= 0.1+ 62 x 0.005 =0.28ohm

Reactance = X1+K2X2= 0.30+ 62 x0.015 = 0.84ohm

Impedance = √0.282+0.842

=0.880hm

Ii)                 Referring to Low voltage sides

Resistance= R1/K2+R2= (0.1/62) + 0.005=0.007ohm

Reactance = Reactance HV side/K2=0.84/62=0.013ohm

Impedance = Impedance referring HV/K2= 0.88/62 = 0.024ohm

Q14) When a transformer is connected to a 1200v,50Hz supply the core loss is 900 W, of which 600 is hysteresis and 350 W is eddy current loss. If the applied voltage is raised to 2000V and frequency to 100 Hz. Find new core losses.

A14) Hysteresis Loss(Wh) α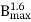 f =P f

Eddy current Loss(We)α P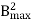 f2 = Q f

The emf equation of transformer is given as E= 4.44fNBmaxA

Bmaxα E/f

So, the above equations become Wh = P (E/f)2 f = P E1.6f-0.6

600= P x 12001.6 x 50-0.6

P=0.074

The eddy current loss               We= Q (E/f)2f2 = QE2

350=Q x 12002

Q=0.243 x 10-3

Now the applied voltage is raised to 2000V so finding new losses with above found P and Q

Wh = P E1.6f-0.6 = 0.074 x 20001.6 x 100-0.6 = 893.06W

We= QE2 = 0.243 x 10-3 x 20002 = 972 W

Q15) A 3-Ø, 50Hz transformer has delta connected primary and star-connected secondary, the line voltage being 20,000 V and 500 V respectively. The secondary has a star connected balanced load at 0.8 lagging p.f. The line current of primary side is 5A. Determine the current in each coil of the primary and secondary line. Also find the output of the transformer?

A15) Phase voltage on primary side = 20,000 V

Phase voltage on secondary = 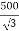V

K =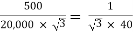

Primary phase current =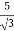

Secondary phase current =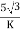

=

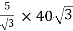
= 200 A

Output = 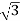VLILcosØ

=

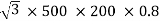
= 138.56 Kw

Q16) A 100 kVA, 3Ø, 50 Hz, 3500/500 V transformer is Δ – connected on the h. V side and Y-connected on the L.V. Side. The resistance of h.V. Winding is 3.5 Ω / phase and that of L.V is 0.02 Ω per phase. Calculate the iron losses of the transformer at normal voltage and frequency if its full load efficiently be 95.1 % at 0.8 p.f.?

A16) Full load output = 100 × 0.8 = 80 kW

Input = 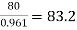kW

Total loss = Input – Output

= 83.2 – 80

= 3200 kW

K =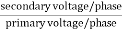

K =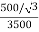

=

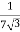
RO2 = R2 + k2R1

=

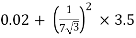
= 0.044 Ωs

Full-load secondary phase current I2

=

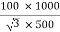
= 115.4 A

Total Cu Loss = 3I22RO2

= 3 × 0.044 × (115.4)2

= 1760 W

Iron Loss = Total loss – Cu Loss

= 3200 – 1760

= 1440 W

Q17) Explain Start-star and delta-delta connection of three phase transformer?

A17) Star – star or Y/Y connection:

The below figure shows transformers connected in Y/Y on both primary and secondary sides. The ratio of line voltage and transformation ratio of line voltage and transformation ratio of both primary and secondary of each transformer in same. Hence the phase voltage VP = 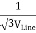  .  VLine (line voltage)

This connection works only if the load is balanced.

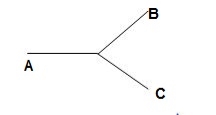
Fig: Three phase transformer Y-Y connection

• The effect of unbalanced load can be balanced by placing single load between a and n on secondary.
• Power to load is supplied by primary side A.
• As, A is in series with B and C and has b and c open on secondary, so it cannot supply required power.
• Now, B and C acts as high impedance in this condition, allowing very less flow of current in A.
• A low resistance can be connected between a and n which is approaching to short circuit. So, small current flows.
• Hence, EAN will reduce to zero but EBN and ECN will rise to full primary line voltage.
• The above shown connection is most economical for small, high-voltage transformers because the number of turns per phase and the amount of installation required is minimum.
• One more advantage is that the installation is stressed to the extent of line to neutral voltage i.e. 58% of line voltage.
• For having a sine wave voltage at output it is necessary that sine wave of flux should be in the core. To fulfil this we require third harmonic component of exciting current.
• To attain this if primary neutral is isolated then triple current cannot be attained. So, the best way is to provide a territory winding to each transformer of 1000 kVA rating.

Delta – Delta or Δ – Δ connection:

• In this connection the ratio of transformation between both primary and secondary line voltage is same.
• There is no internal phase shift between phase and line voltages on either side as it was in                                     Y-Y connection.
• The third harmonic component of current can flow in the Δ-connected transformer primaries.
• The balancing of load is easy unlike Y-Y connections.
• As the phases are 120˚ apart w.r.t. Third harmonic, the flux is sinusoidal which results in sinusoidal voltages.
• If anyone transformer becomes disabled. The system can continue to operate in open delta or V-V connection.

Fig: Δ-Δ connection

Q18) What is voltage regulation of transformer explain?

A18) It can be explained in terms of various parameter of transformer.

(1). When transformer has constant primary voltage.

In this case secondary voltage decreases

0V2 = No-load secondary terminal voltage

0V2 = E2 = EK1 = KV1

V2 = secondary voltage on full-load.

Voltage Regulations is change in secondary terminal voltage from no-load to full load per unit full load voltage.

% regn down = 0V2 – V2/0V2 x 100

% regn up = 0V2 – V2/V2 x 100

(2). Voltage regulation in terms of primary values.

The secondary no-load terminal voltage as referred to primary is E’2 = E2/K = E1 = V1

For secondary full load voltage referred to primary is V’2 = V2/K

% regn = V1 – V’2/V1 x 100

% regn = I1 R01 cosφ + I1 X01 sinφ / V1 x 100

(3). As the transformer is loaded, to maintain a constant output voltage, the primary voltage should be increased. Here the regulation is given as

% regn = V’1 – V1 / V1 x 100

It can also be defined as the change in primary voltage from no-load to full-load at given power factor to maintain a constant output per unit primary voltage.

Q19) Draw the circuit of equivalent transformer circuit and derive expressions?

A19) The basic transformer and its equivalent circuit both are shown below,

Fig. Equivalent   Transformer   Circuit

Iµ - magnetising component of current

Iw = working component

R0 – Non- inductive resistance

I0 – No load current

X0 = E1/I0.  R0 = E1/Iw

E2/E1 = N2/N1 = K

E’2 = E2/K = E1

V’2 = V2/K

I’2 = K I2

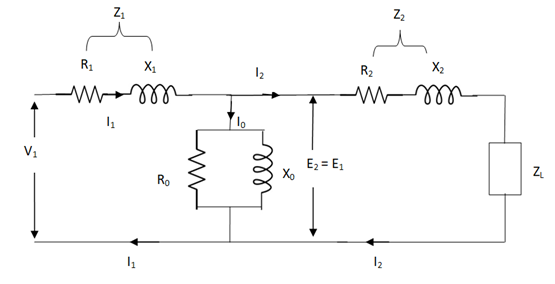
The total equivalent circuit is again given as,

But the above circuit is exact equivalent but harder to solve so, it can be further simplified as,

Fir 4 More Simplified Equivalent Circuit

Z = Z1 + Zm || ( Z’2 + Z’L )

= Z1 + Zm(Z’2 + Z’L)/Zm + (Z’2 + Z’L)

Z’2 = R’2 + jX’2

Zm = impedance of exciting circuit

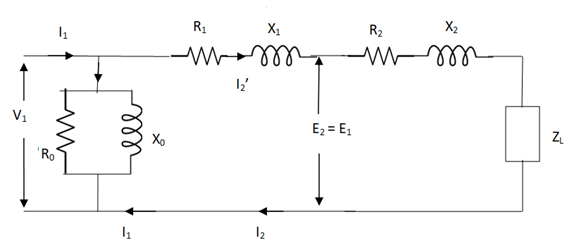
V1 = I1[ Z1 + Zm(Z’2 + Z’L) / Zm + (Z’2 + Z’L) ]

Q20) Draw and explain the BH characteristics of magnetic material?

A20) In a magnetic circuit, this field is represented by magnetomotive force. It is analogous to the electromotive force in electrical circuit. This field is responsible to “set up” certain flux, which in turn gives rise to certain flux density B. Note that, here H is cause and B is its effect. The amount of flux which can be setup in a material is determined by an inherent property of the material, called as permeability, denoted by µ.

B = µH

When external magnetic field H is applied to a material, all the domains align in a particular direction, setting up net flux in the material. Due to domain alignment B (i.e. the magnitude of B) increases. However, after a certain value of B, the slope of B − H curve starts reducing as shown in Figure below

Fig: Magnetization curve

B-H Curve:

We cannot measure B and H directly. Further if we have transformer, we only have terminal measurements are with us. Hence, it is required to process the signals to get values of B and H. From Faraday’s law, V = N dφ/dt . Also, B is directly proportional to flux φ.

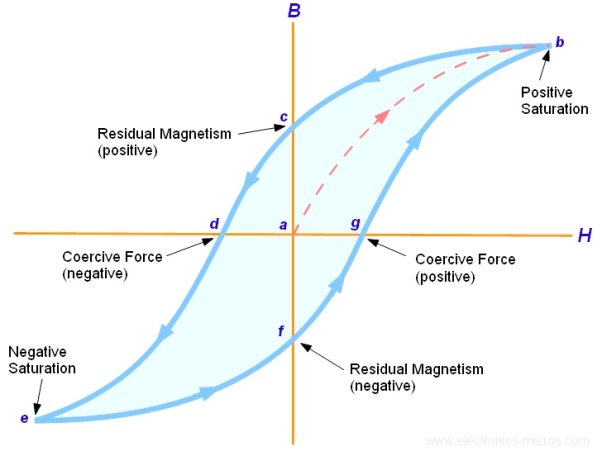
Fig: B-H curve

The lag or delay of a magnetic material known commonly as Magnetic Hysteresis. The Magnetic Hysteresis loop above, shows the behaviour of a ferromagnetic core graphically as the relationship between B and H is non-linear. Initially both B and H will be at zero, point 0 on the magnetisation curve.

If the magnetisation current, i is increased in a positive direction to some value than the magnetic field strength H increases linearly with i and the flux density B also increases (curve from point 0 to point a) as it heads towards saturation.

Now if the magnetising current in the coil is reduced to zero, the magnetic field circulating around the core also reduces to zero. However, the coils magnetic flux will not reach zero due to the residual magnetism present within the core and this is shown on the curve from point a to point b.

To reduce the flux density at point b to zero we need to reverse the current flowing through the coil. The magnetising force which must be applied to null the residual flux density is called a “Coercive Force”. This coercive force reverses the magnetic field re-arranging the molecular magnets until the core becomes unmagnetized at point c.

An increase in this reverse current causes the core to be magnetised in the opposite direction and increasing this magnetisation current further will cause the core to reach its saturation point but in the opposite direction, point d on the curve.

This point is symmetrical to point b. If the magnetising current is reduced again to zero the residual magnetism present in the core will be equal to the previous value but in reverse at point e.

Again, reversing the magnetising current flowing through the coil this time into a positive direction will cause the magnetic flux to reach zero, point f on the curve and as before increasing the magnetisation current further in a positive direction will cause the core to reach saturation at point a.

Then the B-H curve follows the path of a-b-c-d-e-f-a as the magnetising current flowing through the coil alternates between a positive and negative value such as the cycle of an AC voltage. This path is called a Magnetic Hysteresis Loop