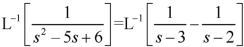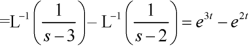Unit – 1

Laplace Transformation

Q1) What is Laplace transform?

A1)

Let f(t) be any function of t defined for all positive values of t. Then the Laplace transform of the function f(t) is defined as-

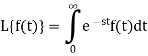
Provided that the integral exists, here ‘s’ is the parameter that could be real or complex.

The inverse of the Laplace transform can be defined as below-

Here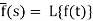

f(t) is called the inverse Laplace transform of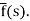

L is called the Laplace transformation operator.

Q2) Find the Laplace transform of the functions  

A2)

Here

So that we can write it as-

Now-

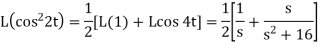
Q3) Find the Laplace transform of (1 + cos 2t)

A3)

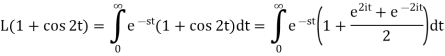
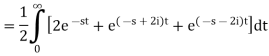
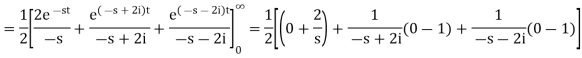
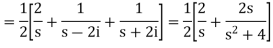
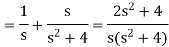
So that-

Q4) What is the linearity property of LT?

A4)

Let a and b be any two constants and 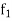, any two functions of t, then-

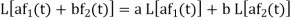
Proof: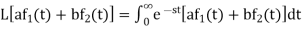

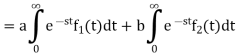
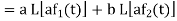
Hence proved.

Q5) Find the Laplace transform of t sin at.

A5)

Here-

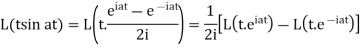
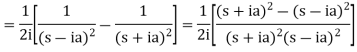
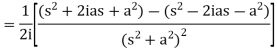
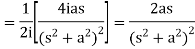
Q6) Find the Laplace transform of the following function-

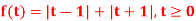
A6)

The given function f(t) can be written as-

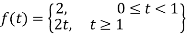
So, by definition,

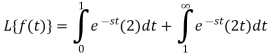
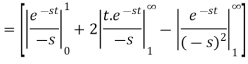
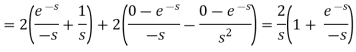
Q7) What do you understand by periodic function?

A7)

Suppose the function f(t) be periodic with period , then-

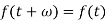
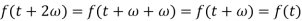
Similarly-

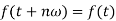
Now-

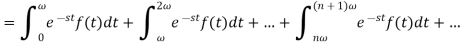
Put t = z + in the second integral of the above equation and t = z + 2 in the third integral and so on.

We get-

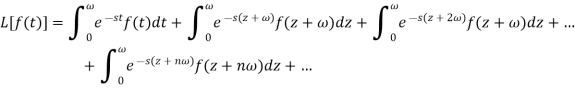
F(t) is periodic with period we can write-

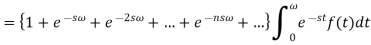
Here 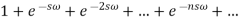is a geometric progression with a common ratio 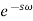, and we know that the sum of infinite terms in G.P. Is given by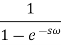
 

Then-

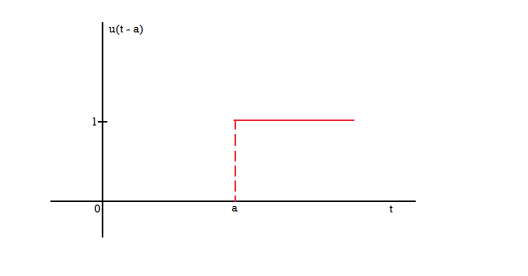
Q8) Define unit step function.

A8)

Unit step function

The unit step function u(t – a) is defined as-

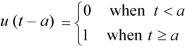
Laplace transform of unit functions-

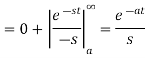
Q9) Find the Laplace transform of the following function by using unit step function-

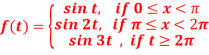
A9)

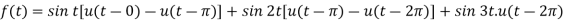
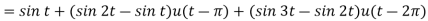
Since

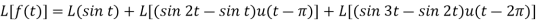
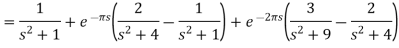
Q10) Evaluate-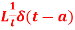

A10)

As we know that-

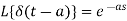
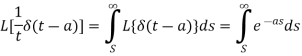
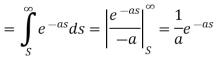
Q11) Find the inverse Laplace transform of-

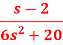
A11)

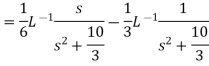
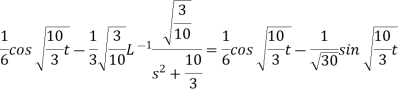
Q12) Find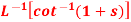

A12)

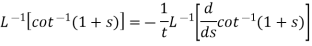
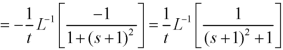
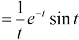
Q13) Find the Laplace inverse of-

A13)

We will convert the function into partial fractions-

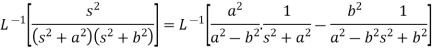
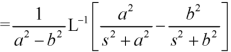
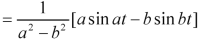
Q14) Find

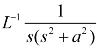
A14)

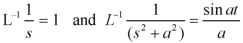
Therefore by the convolution theorem-

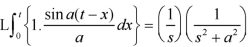
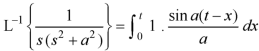
Q15) Use Laplace transform method to solve the following equation-

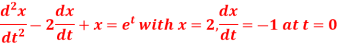
A15)

Here we have-

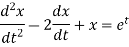
Take Laplace transform of both sides, we get-

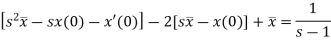
It becomes-

(

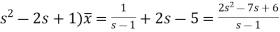
So that-

Now breaking it into partial fractions-

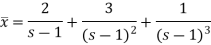
We get the following results on inversion-

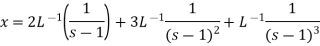
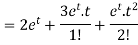
Q16) Use Laplace transform method to solve the following equation-

A16)

Here we have-

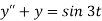
Taking Laplace transform of both sides, we get-

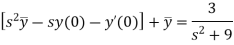
We get on putting given values-

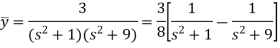
On inversion, we get-

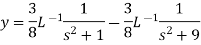
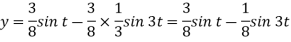
Q17) solve the following differential equation by using Laplace transform-

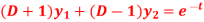
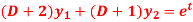
Here D = d/dt and

A17)

Here we have-

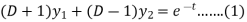
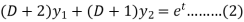
Now multiply (1) by D+1 and (2) by D – 1 we get-

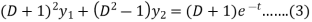
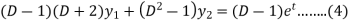
Now subtract (4) from (3), we get-

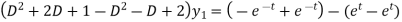
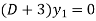
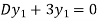
By taking Laplace to transform we get-

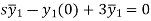
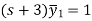
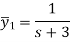
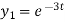
Put the value of 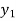in (1) we get-

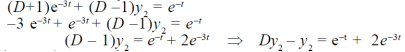
By taking Laplace to transform we get-

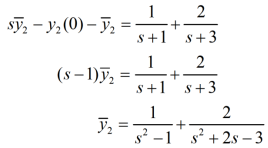
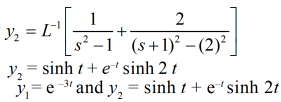
Which is the required answer.

Q18) Find the inverse transform of-

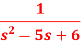
A18)

First, we will convert it into partial fractions-