Unit – 3

Z-Transform & Inverse Z-Transform

Q1) Define Z-transform.

A1)

The Z-transform can be defined as either a one-sided or two-sided transform.

Bilateral Z-transform

The bilateral or two-sided Z-transform of a discrete-time signal {\displaystyle x[n]}x(n) is the formal power series {\displaystyle X(z)}X(z) defined as

X (z) = Z =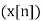

Where {\displaystyle n}n is an integer and z{\displaystyle z} is, in general, a complex number:

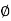{\displaystyle z=Ae^{j\phi }=A\cdot (\cos {\phi }+j\sin {\phi })}where {\displaystyle A}A is the magnitude of z,j{\displaystyle z} {\displaystyle j} is the imaginary unit and {\displaystyle \phi } is the complex argument (also referred to as angle or phase) in radians.

Unilateral Z-transform

Alternatively, in cases where {\displaystyle x[n]}x[n] is defined only for {\displaystyle n\geq 0} the single-sided or unilateral Z-transform is defined as

X (z) = Z =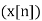

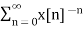
Q2) What is time shifting property?

A2)

Time Shifting Property

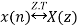
Then the time-shifting property states that

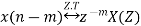
Multiplication by Exponential Sequence Property

If x(n)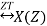

Then multiplication by an exponential sequence property is

Q3) What are the Properties of ROC of Z-Transforms

A3)

• ROC of z-transform is indicated with a circle in z-plane.
• ROC does not contain any poles.
• If x(n) is a finite duration causal sequence or right-sided sequence, then the ROC is entire z-plane except at z = 0.
• If x(n) is a finite duration anti-causal sequence or left-sided sequence, then the ROC is the entire z-plane except at z = ∞.
• If x(n) is an infinite duration causal sequence, ROC is the exterior of the circle with radius a. i.e. |z| > a.
• If x(n) is an infinite duration anti-causal sequence, ROC is the interior of the circle with radius a. i.e. |z| < a.
• If x(n) is a finite duration two sided sequence, then the ROC is entire z-plane except at z = 0 & z = ∞.

Q4) Find Z-transform of the following function-

A4)

Q5) Find Z-transform of the following function-

A5)

As we know that-

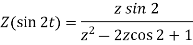
So that-

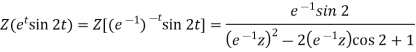
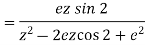
Q6) Find the z-transformation of the following left-sided sequence

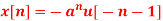
A6)

= 

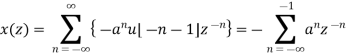
= 1-

=

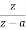
If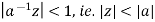 

Q7) Find the Z-Transform of log (z / z + 1) by using power series method.

A7)

Taking, z = 1/t, U(z) =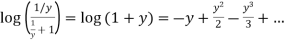

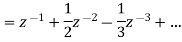
Thus

Q8) Find the Z-Transform of 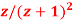by using division method.

A8)

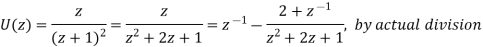
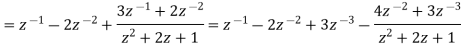
Continuing this process of division, we obtain an infinite series,

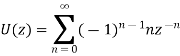
Thus

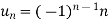
Q9) Find the Z-Transform of

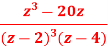
A9)

Writing,

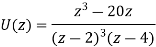
As

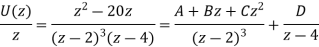
We get D = ½. Multiplying throughout by 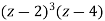, we get

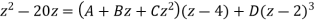
Putting z = 0, 1, -1 successively and solving the resulting simultaneous equations, we get

A = 6, B = 0 and C = ½

Thus

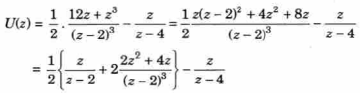
On inversion, we get

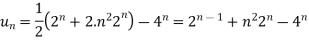
Q10) Find the z-transform of x(n) = [3(3) n – 4(2) n ] u(n)

A10)

X(z) =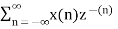

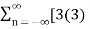= n – 4(2) n ] u(n) z -n

= n – 4(2) n ] u(n) z -n

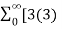=n z -n   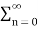- 4(2) n ]  z -n

=3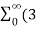 z -1 ) n – 4  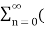  2 z -1 ) n

The first power series converges when |3z -1| <1 that is |z| > 3 . The second power series converges when |2z-1| <1 or |z| >2. Hence X(z) converges for |z|>3 .

Now X(z) = 3/1-3z-1 -4/1-2z-1

= 3z/z-3 – 4z/z-2

Q11) State and prove convolution theorem.

A11)

Statement:

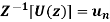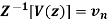According to the convolution theorem if and then

Proof:

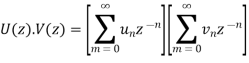
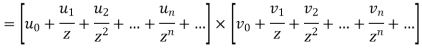
Collecting the coefficients of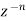

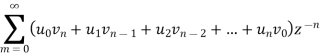
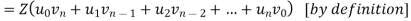
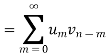
Q12) What is region of convergence?

A12)

The region of convergence of Z-transform is the region in the z-plane where the infinite series convergence absolutely.

Thus the region of convergence of a one-sided Z-transform

Of a right-sided sequence, which means,

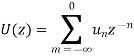
Is |z| > a i.e., the exterior of the circle with centre at origin and of radius a.

Similarly the region of convergence (ROC) of

Is the annulus region a < |z| < b.

Q13) Solve the differential equation 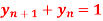 by the z-transformation method.

A13)

Given,

Let y(z) be the z-transform of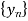

Taking z-transforms of both sides of eq(1) we get,

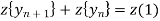
Ie.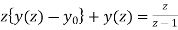

Using the given condition, it reduces to

(z+1)y(z) =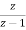

i.e.

Y(z) =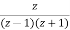

Or Y(Z) =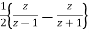

On taking inverse Z-transforms, we obtain

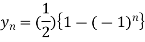
Q14) Solve 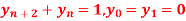using z-transforms.

A14)

Consider,

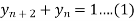
Taking z-transforms on both sides, we get

=

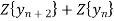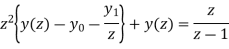
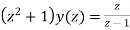or

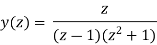
Now,

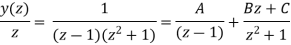
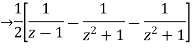
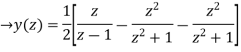
Using inverse z-transform we obtain,

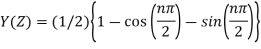
Q15) Solve the following by using Z-transform

A15)

If 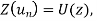then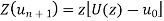

And

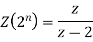
Now taking the Z-transform of both sides, we get

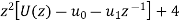z[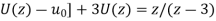

It becomes-

So,

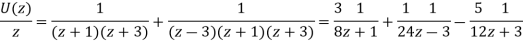
Now-

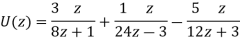
On inversion, we get-

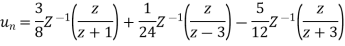
Q16) Determine the z-transform of the signal

x(n ) = rn (sin w0n ) u(n)

A16)

Z{(sin w0n ) u(n)}  = sin w0 z-1/ 1 -2 (cos w0) z-1 + z-2

Z{ an x(n)} = X(a-1 z)

Therefore

Z{ rn sin(w0n) u(n) } = (sin w0) (r-1 z)-1/ 1- 2 (cos w0)(r-1z)-1 + (r-1z)-2  

= r(sinw0) z-1/ 1-2r(cos w0) z-1 + r2 z-2

Q17) What is final value theorem?

A17)

If X+(z) = Z{x(n)} where ROC for X+(z) includes but is not necessarily confined to |z| >1 and (z-1) X+(z) has no poles on or outside the unit circle then

x(∞) = Lim z->1 (z-1) X+(z)

Z{ x(n+1) – Z{x(n)} = Lim k-> ∞ 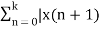  - x(n)]z-n

Z X+(z) – z x(0) – X+(z) = Lim k-> ∞ 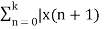  - x(n)]z-n

(z-1) X+(z) – zx(0) =  Lim k-> ∞ 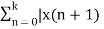  - x(n)]z-n

Let z-> 1 we get

Lim z->1 (z-1) X+(z) – zx(0) = Lim k-> ∞ 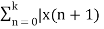  - x(n)]

Lim z->1 (z-1) X+(z) – x(0) = Lim n-> ∞ { [x(1) -x(0)] + [x(2) -x(1)] +……+[x(n+1)-x(n)]}

= x(∞) – x(0)

Therefore,

x(∞) = limz->1 (z-1) X+(z)

This can be written as

x(∞) = lim z->1 (1-z-1) X(z)