Unit - 1

Introduction to LTI elements

Q1) Write equation for given waveform

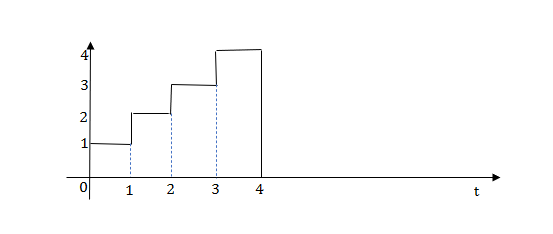
A1)

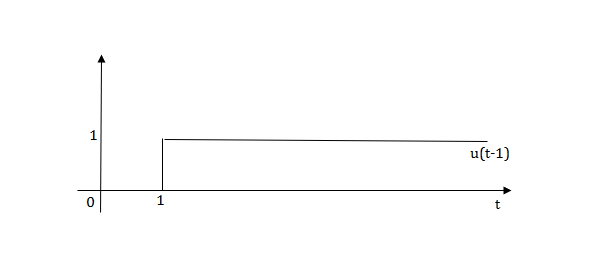
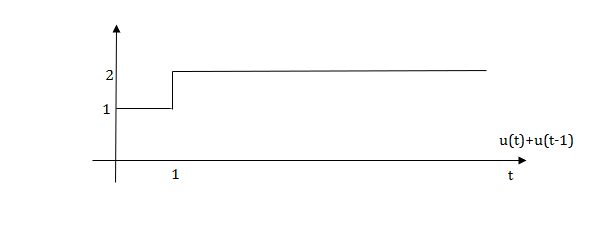
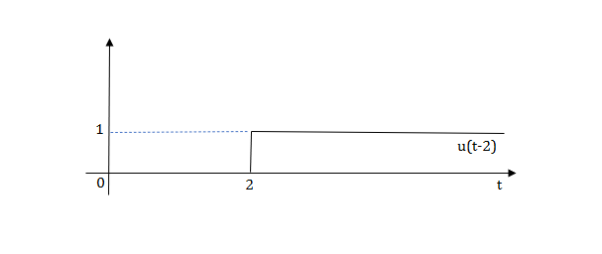
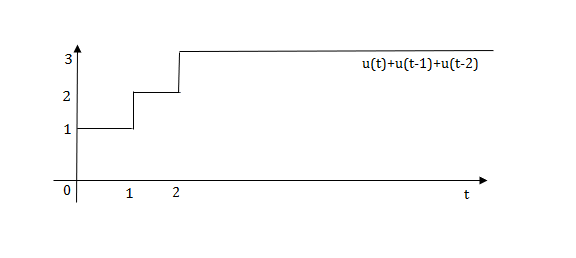
The final equation is=u(t)+u(t-1)+u(t-2)+u(t-3)-4u(t-4)

As the waveform is stopped at t=4 with amplitude 4,so we have to balance that using -4u(t-4).

Q2) Write the equation for the given waveform?

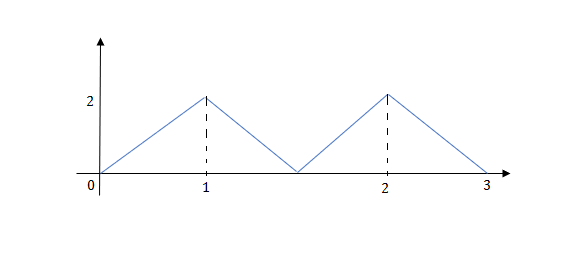
A2) Calculating slope of above waveform

Slope for (0,0) and (1,2)

a1 slope=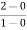=2

a2 slope=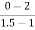=-4

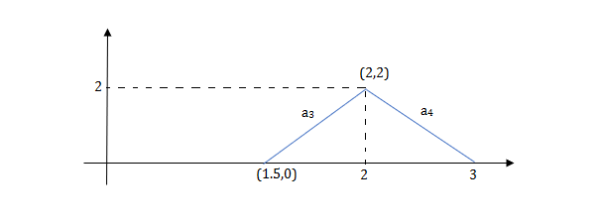
a3 slope =4 and a4= -2

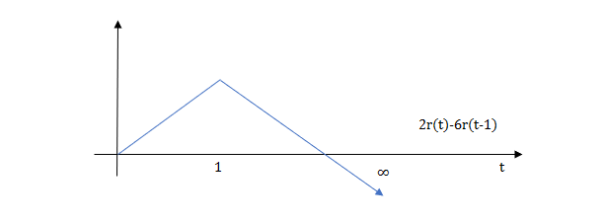
At t=1 slope changes from 2 to -4 so we need to add -6r(t-1) to 2r(t) to get the slope of -4.

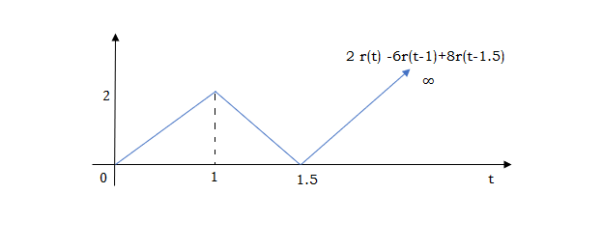
At t=1.5 slope changes from -4 to 4 so adding 8r(t-1.5) to get slope of 4

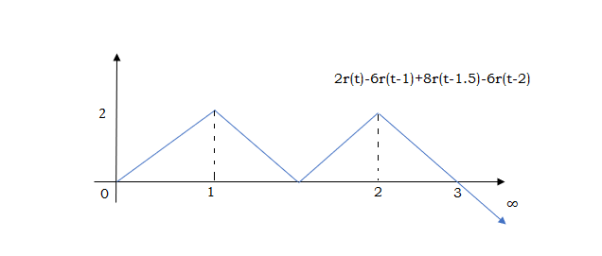
At t=2 slope changes from +4 to -2 so we add -6r(t-2). But we need to stop the waveform at t=3. Hence, we have to make slope 0. Which can be done by adding +2r(t-3). Final equation is given as 2r(t)-6r(t-1.5) +8r(t-1.5)-6r(t-2) +2r(t-3)

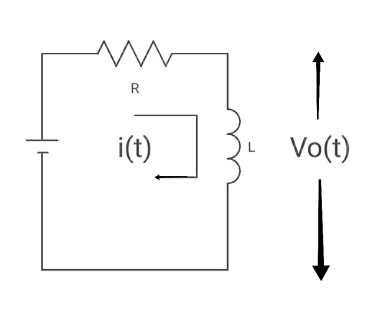
Q3) For given RL circuit find the differential equation for current i?

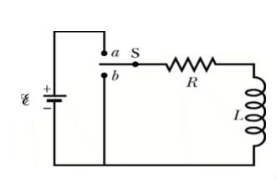
Fig: Series RL circuit

A3)

After switch is closed applying KVL

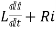=0

This is first order homogeneous differential equation so

dt

Integrating both sides

Ln i= t+K

Taking antilog of both sides

i=k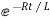

At t=0

i(0)==I0

=ke0

The particular solution is given as

i= 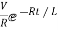       for t≥0

=for t<0

Q4) Find IL(0) for the given circuit below

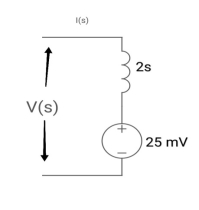
A4) From above circuit

L = 2H

LiL (0) = 25 mv

IL (0) = 12.5 m A

Q5) Find value across capacitor?

A5) From above circuit we can write

1/cs = 2/s

C=1/2f

Vc (0)/s = 0.25v/s

Vc(0)= .25v

Q6) Find voltage across capacitor?

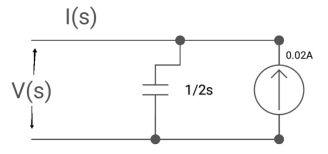
A6) 1/cs = 1/2S

C=2F

CVc (0) = 0.02

Vc(0)= 0.01V

Q7) For the following circuit shown below

(a)  switch is at before moving to position = at t= 0, at t= 0+, i1(t) is

(a)  –V/2R (b) –V/R (c) – V/4R

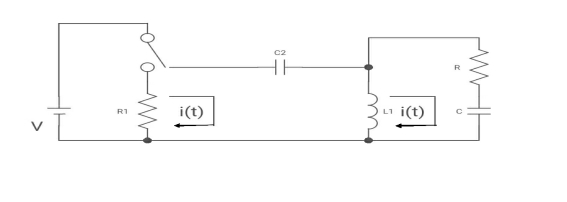
A7)

I1(t) L.T    I1(s)

I2(t) L.T    I2(s)

Then express in form

[ I1(s)/I2(s)] [::] = [:]

Drawing the ckl at t = 0-

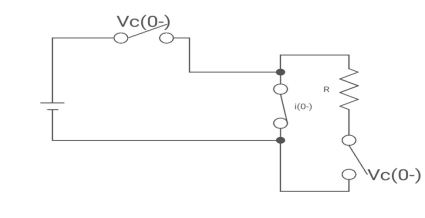
:. The capacitor is connected for long

Vc1(0-)= V

iL(0-) =0

Vc2(0-)=0

At t= 0+

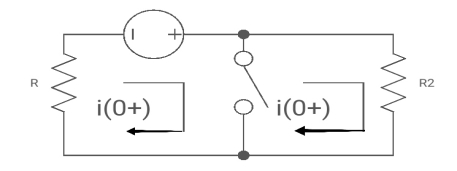
i1 (0+) = -V/2R

For t>0 the circuit is

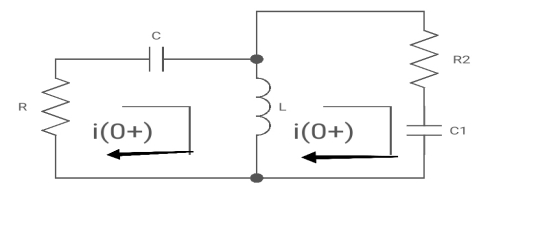
Apply KVL

-R i1(t) -1/c dt -L=0

Also, we can deduce i1(t)- i2 (t) = iL(t)

-Ri1(t) -1/c - L = 0

-RI1(s)-[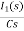-]-L[sI1(s)-iL(0-)]=0

- RI1(s)-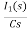 - -s L I2(s)=0

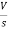- s L I2(s)= -                      (1)

Again

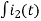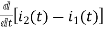-Ri2(t) ) -1/c dt -L=0

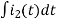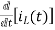-Ri1(t) -1/c - L = 0

Taking Laplace Transform

-RI2(s)- [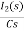  -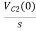]- L[s IL(s)- iL(0-)]=0

-RI2(s)- 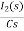  -Ls[ I1(s)- I2(s)]=0

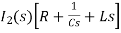- s L I1(s)=0                         (2)

Hence in matrix representation

=

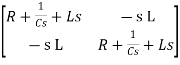
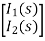Q8) All initial conditions are zero i(t) L.T, I(s), then find I(s)?

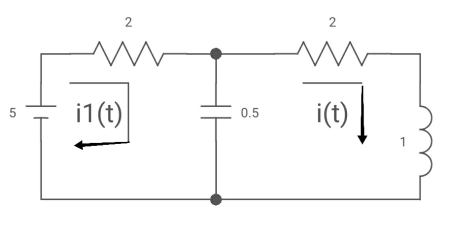
A8) Drawing Laplace circuit

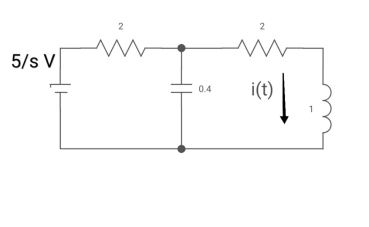
(2+S) 11 2/S

Zeq = [(2+S)2/S]/[2+S+2/S]=[2(S+2)]/[S2+2s+2]

V1(s) = [5/S{2(S+2)/S2+2S+2}]/[2+{2(S+2)/ S2+2S+2}]

V1(s) = [5(S+2)/S]/[S2+ 3S +4]

I(s) = V1(s)/(S+2) = (5/S)/(S2+35+4)

Q9) The switch is at before moving to position = at t= 0, at t= 0+, i1(t) is

(a)  –V/2R (b) –V/R (c) – V/4R (d) 0

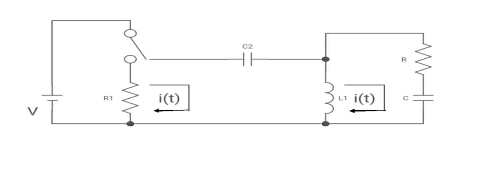
A9)

I1(t) L.T    I1(s)

I2(t) L.T    I2(s)

Then express in form

[ I1(s)/I2(s)] [::] .[:]

Drawing the ckt at t = 0-

:. The capacitor is connected for long

Vc1(0-)= V

iL(0-) =0

Vc2(0-)=0

At t= 0+

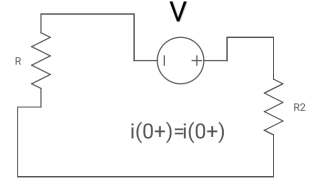
Fig: Circuit at t=0+

i1 (0+) = -V/2R

For t>0 the circuit is

Fig: KVL in Circuit

Apply KVL

-R i1(t) -1/c dt -L=0

Also, we can deduce i1(t)- i2 (t) = iL(t)

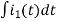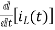-Ri1(t) -1/c - L = 0

-RI1(s)-[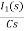-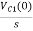]-L[sI1(s)-iL(0-)]=0

- RI1(s)- - -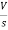s L I2(s)=0

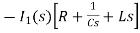- s L I2(s)= -  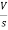                    (1)

Again

-Ri2(t) ) -1/c 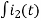dt -L=0

-Ri1(t) -1/c 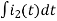- L = 0

Taking Laplace Transform

-RI2(s)- [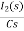  -]- L[s IL(s)- iL(0-)]=0

-RI2(s)- 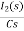  -Ls[ I1(s)- I2(s)]=0

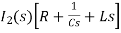- s L I1(s)=0                         (2)

Hence in the matrix representation

=

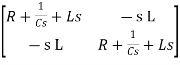
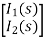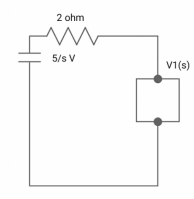
Q10) All initial conditions are zero i(t) I(s), then find I(s)?

A10) Drawing Laplace circuit

(2+S) 11 2/S

Zeq = [(2+S)2/S]/[2+S+2/S]=[2(S+2)]/[S2+2s+2]

V1(s) = [5/S{2(S+2)/S2+2S+2}]/[2+{2(S+2)/ S2+2S+2}]

V1(s) = [5(S+2)/S]/[S2+ 3S +4]

I(s) = V1(s)/(S+2) = (5/S)/(S2+35+4)

Q11) There is no initial energy stored in this circuit. Find i1(t) and i2(t) for t>0?

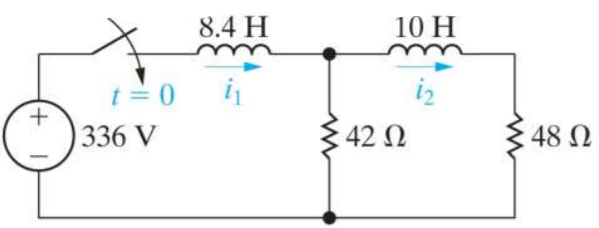
A11)

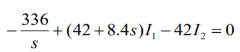
When circuit is closed the network is shown

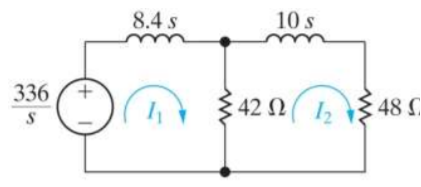
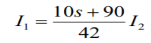
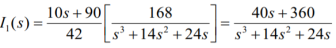
Q12) Find v0 (t) for t > 0.

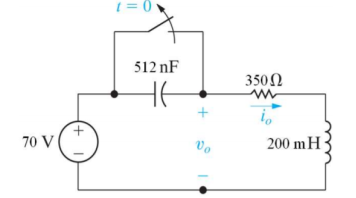
A12) Taking Laplace transform of above circuit we have,

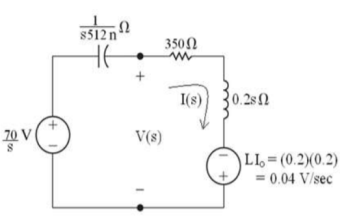
Q13) There is no initial energy stored in this circuit. Find vo if ig = 5u(t) mA.

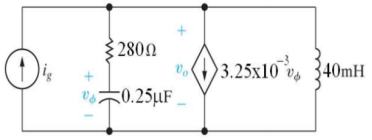
A13) Laplace Transform of above circuit we get

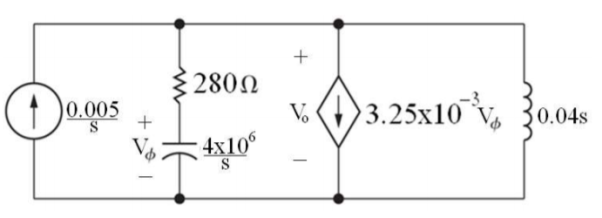
By voltage division we get

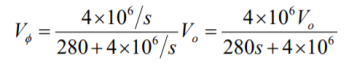
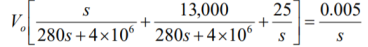
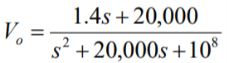
Q14) Find value of current i(t) for the given circuit?

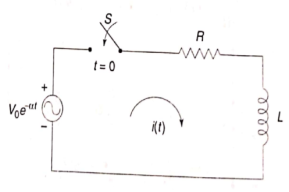
A14)

Applying KVL we get

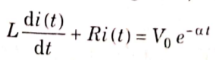
Taking Laplace transform of above equation we get

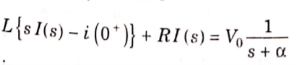
There is no initial current in inductor before closing the switch so i(0+)=0.

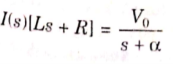
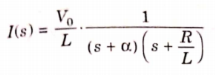
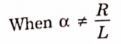
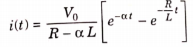
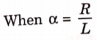
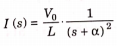
Taking ILT we get

Q15) For the circuit shown below find the value of i1(t) and i2(t) and output voltage across 5 Ohm resistor when the switch is closed also find initial and final values of current?

A15) By KVL we have

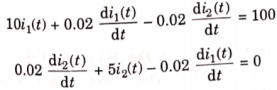
Taking LT of above equations, we get

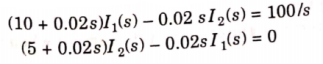
Solving above equation we get

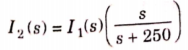
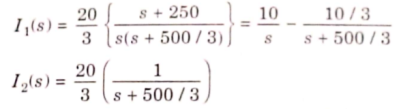
By inverse Laplace transform we get

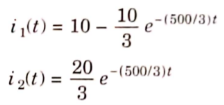
The voltage across 5 Ohm resistor is

The initial value of i1(t) is

The final value of i2(t) is

The initial value of i2(t) is

The Final value of i2(t) is

Q16) Find the inverse Laplace transform of

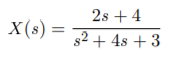
A16)

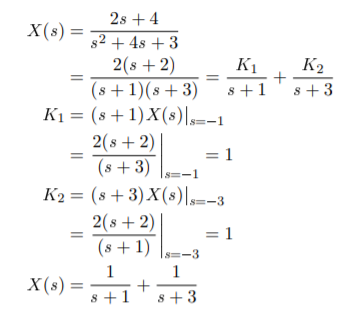
We know that

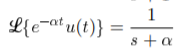
Hence,

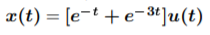
Q17) Find inverse Laplace transform of

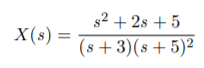
A17)

Taking inverse Laplace of above we get

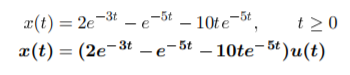
Q18) Find Inverse Laplace transform of

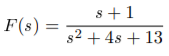
A18)

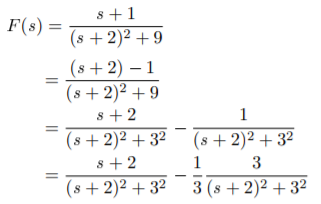
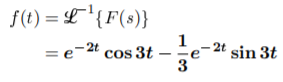
Q19) Find Inverse Laplace Transform of

A19)

Q20) Write equation for initial and final value theorem?

A20) The initial value theorem

This theorem is valid if and only if f(t) has no impulse functions.

The final value theorem

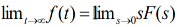
This theorem is valid if and only if all but one of the poles of F(s) are in the left-half of the complex plane, and the one that is not can only be at the origin.

Q21) V0 (t) = ? t =o if capacitor is uncharged?

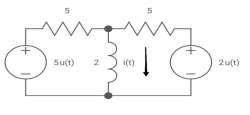
A21) We know i(t) = i(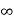)+[ i(0)- i()]

Req = R1R2 /R1+R2=(5x5)/(5+5)=5/2ohm

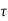=L/Req=4/5 sec

i(0)=0

i()=u(t)+u(t)=1.4u(t)

i(t)=1.4[1-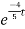]u(t)

Q22) Find Vo(t) for the circuit below?

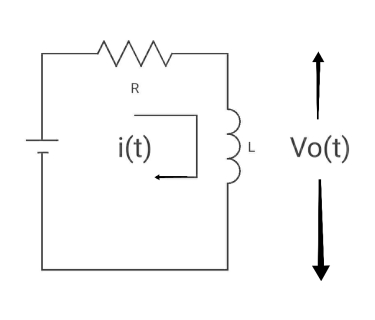
A22)

Time constant 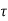=L/Req = L/R

V () = 0, V (0) =VR (supply voltage)

i () = VR/R, i(0) =0

By KVL,

VR=i(t) R + L di/dt(t)

On solving

V0(t)= VR e-tR/L

Q23) In network below switch is moved from 1 to 2 at t=0 a steady state is achieved already. Fond capacitor voltage Vc(t) and current i(t) through 200Ω?

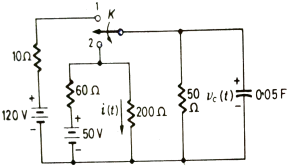
A23) The Voltage across capacitor is given by

Vc(t)= K1+K2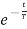

The steady state is reached when t= the above equation becomes

Vc(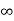)= Lt t--> 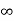K = K1

At t=0

Vc(0)= K1+K2

K2= Vc(0)- Vc()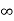

The final response for the circuit is given as

Vc(t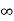)= Vc(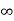)-[Vc()-Vc()]

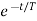
When switch is at position 1

Vc(0)= x 50 = 100V

So, voltage of capacitor at t=0 and t=0+ will remain same.

TO find Req we replace voltage source by short circuit

Req = 60||200||50 = 24 Ω

The time constant will be T = ReqC = 24x0.05 = 1.2sec

Switch at position 2

The steady state voltage across capacitor is given by

= +

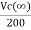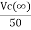
Vc(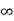) = 20V

The complete response will be

Vc(t)= V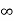c(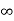)-[Vc()-Vc()]

Vc(t)= 20 –[20-100]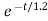

Vc(t)= 20+ 80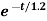

The value of current at switch position 1

I= 50/(200+60) = 0.192A

When switch is at 2

i(0+) = 100/200= 0.5A

i(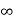) = Vc(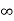) /200 = 0.1A

The complete response of current is

i(t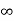)= i()-[i()-i()]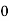

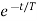
i(t)= 0.1-[0.1-0.5]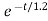

i(t)=0.1+0.4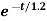

Q24) Find the value of V0(t) for circuit below?

A24)

Time constant, c= L/Req = L/R

V(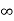) = 0

V(0) = VR

i() = VR/R

i(0) =0

By KVL,

VR=i(t) R + L di/dt(t)

On solving

V0(t)= VR e-tR/L

Q25) Find iL(t) for the circuit below. For t>0?

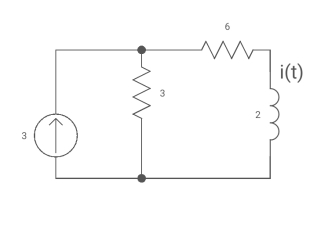
A25) The circuit for Req will be

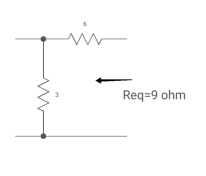
Req = 6+3

= 9ohm

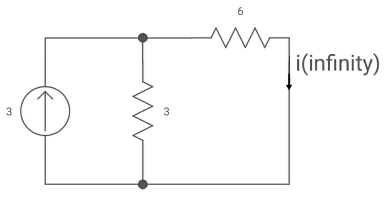
T= L/Req = 2/9 sec

i(0) =0

i() = 3*3/6+3 = 1A

i(t) = 1 [1-e4.5t]

Q26) Capacitor is initially uncharged find Vc (t); t >0

A26)

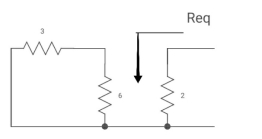
Req = (3116)+2

=2+2 = 4ohm

T= C Req= 2 sec

Clearly Vc(0) =0

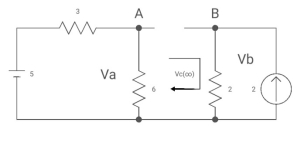
By voltage divides, VA  = 5*6/3+B = 30 v/9

Clearly by ohms low

VB = 2*2 = 4v

Apply KVL, VA-Vc-VB =0

Vc() = 30/9 – 4 = -2/3 V

Vc (t) = -2/3 [1- e0.25t]

CURVE:

Vc(t) =2/3 [1-e-0.5t]

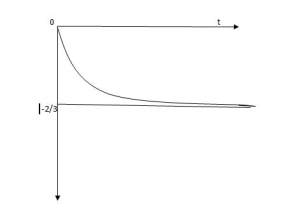
Vc(t) = -2/3 [1-e-0.5t]

Q27) Find i(t) for the given circuit below?

A27) We know i(t) = i () +[i(0)- i()] e-t/T

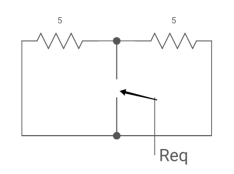
Req = 5*5/5+5 = 5/2 ohm

T=L/Req = 4/5 sec

Also

i(0) =0

i() = u(t) +2/5 u(t)

i(t) = 1.4 [1-e-5/4t)]u(t)

Q28) If switch ‘s’ closed for long time before opening at t=0-. Find Vx (0+)?

A28) At t= 0-   switch was closed,

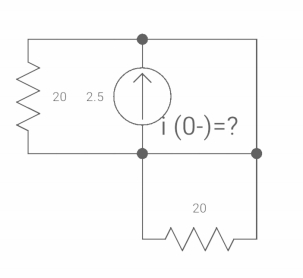
iL(0-) = 2.5A

At t= 0+

Inductor is initially charged so iL(0-) = iL(0+)

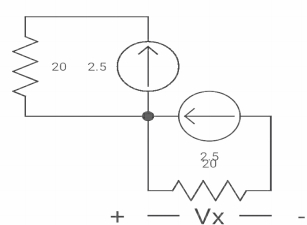
-Vx = 20x2.5

Vx = -50A

Q29) Find VR(0+) and dil/dt(t) = 0+   If switch is opened at t= 0?

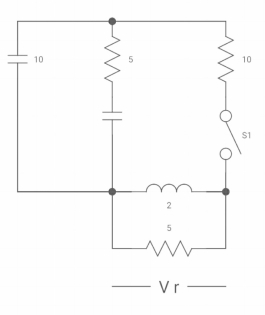
A29) At time t=0-

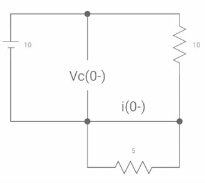
Vc(0-) = 10V

IL(0-) = 10/10 = 1 A

Also, iL(0-) = iL(0+) = 1A

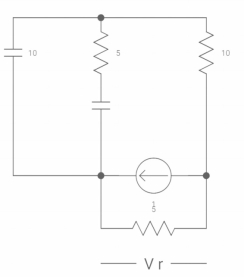
VR(0+) = 5V

Ldi(t)/dt = VL (t)

DiL(t)/dt = VL(t)/L

At t= 0+

d iL (0+) /dt = VL(0+)/L

-VL (0+)-VR =0

VL (0+) = -5V

DiL(t)/dt at t=0+

VL(0+)/L  =-5/2

Dil/dt(o+) = 2.5 A/s

Q30) Find Vc(o+) and iR (o+) it switch‘s’ is closed at t=0?

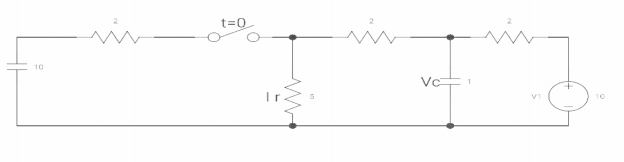
A30) At t=0-

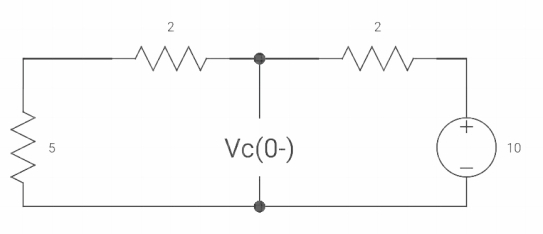
When switch opened at t=0

As capacitor is fully charged so acts as open circuit

Vc (0-) = 7*10/7+2 = 70/9v

At  t=0+

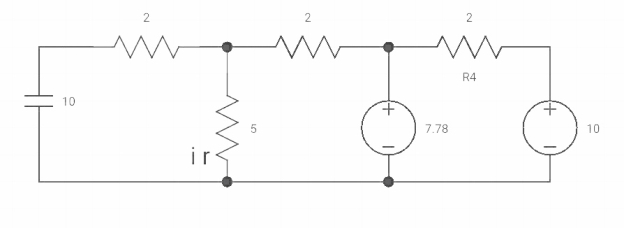
At t=0+ circuit

Vc(0+) = Vc (0) = 40/9v

By applying kcl at A,

VA-10/2+ VA/5+VA-7019/2 =0

VA [1/5+1/2+1/2] = 5+35/9

Va [6/5] = 80/9

Va= 400/54v

IR (0+) = Va/5 = 400/54*5 = 80/54 A

Q31) Find diL(t)/dt and dVc(t)/dt at t=0+. If switch is opened at t=0?

A31) At t=0-

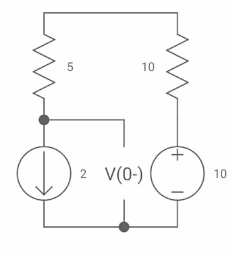
Switch closed for long

Vc(0-) =10V = Vc(0+)

iL(0-) = 2A

DiL(t)/dt = VL(t)/L

At t=0+

DiL(0+)/dt = VL(0+)/L

Similarly, C = ic(t)

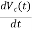= ic(t)/C

At t=0+

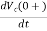= ic(0+)/C

ic(0+) = -2A