Unit - 6

Hurwitz Polynomial

Q1) For the given polynomials find whether they are Hurwitz polynomials or not.

a). F1(S) = S + 3

b). F2(S) = S2 + 5

c). F3(S) = s2 + 5S + 6

d). F4(S) = S3 + 4S2 + 8S + 4

A1)

a). F1(S) = S + 3

S = -3

Its Hurwitz polynomial

b). F2(S) = S2 + 5

S = Ij√5

Its Hurwitz polynomial

c). F3(S) = S2 + 5S + 6

S2 + 5S + 6

S2 + 2S + 3S + 2 x 3

(S + 3)(S + 2)

F3(S) => S = -3, -2

It is Hurwitz polynomial.

d). F4(S) = S3 + 4S2 + 8S + 4

E(S) = 4S2 + 4  O(S) = S3 + 8S

4(s2 + 1 )  S(S2 + 8)

S = Ij   S = Ij2√2

Its Hurwitz polynomial

Q2) Find the range of K for which the polynomial 2S4 + S3 + KS2 + S + 2 is Hurwitz?     

A2)

K > 2, K > 4

K > 4

Q3) Find whether the given function F(S) = S + 4 / S2 + 2S + S is positive real or not?

A3)

By inspection check the function

(ii) Numerator and Denominator should both be Hurwitz

(iii) Real part of function must be positive for all values of W.

N(S) = S + 4  D(S) = S2 + 2S + S

It is Hurwitz  It is Hurwitz

Finding real part of function, S = jw.

F(jw) = jw + 4 / -w2 + 2jw + 5

= 4 / -w2 + 2jw + 5  +  jw / -w2 + 2jw + 5

= 4 + jw/ -w2 + 2jw + 5  x   ( -w2 + 5 - 2jw ) / ( -w2 + 5 - 2jw )

= -4w2 + 20 + 2w2 / (-w2 + 5)2 – (2jw)2

Real part

= 20 – 2w2 / w4 + 4w2 – 102 + 25

= 20 – 2w2 / w4 – 6w2 + 25

For, w1 = 1, 2, …

For w > 3 function becomes negative. So not positive real.

Q4) 8S6 + 4S5 + 34S4 + 16S3 + 32S2 + 12S + 6. Find whether this is Hurwitz or not?

A4)

This is the case of premature termination.

F(S) = F1(S).F2(S)

From above F1(S) = 2S4 + 8S2 + 6

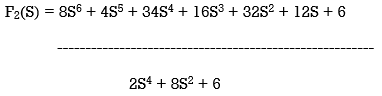
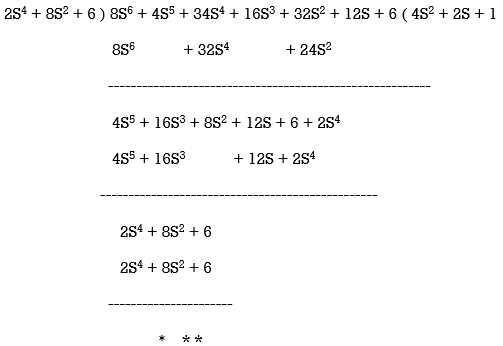
F1(S) = 2S4 + 8S2 + 6 – It is Hurwitz

F2(S) = 4S2 + 2S + 1 – Has one root or RHS

F(S) is not Hurwitz as F2(S) is non Hurwitz.

Q5) For the given function Z(S) = 6S3 + 2S / 9S4 + 4S2 + 1 / 6 realise the network function using Cauer foster.

A5)

Degree of denominator is greater so

Y(S) = 9S4 + 4S2 + 1 / 6 / 6S3 + 2S

Y1(S) = 9 / 6S = CS => C = 9 / 6 = 3 / 2

Z2(S) = 6S => L = 6

1 / 3(S) = S => C = 1

Z4(S) = 6S => L = 6

Q6) For the function Z(S) = S2 + 6S + 8 / S2 + 4S + 3 is RL or RC.

Realise the above function.

A6)

Z(S) = S2 + 6S + 8 / S2 + 4S + 3 = (S+4)(S+2) / (S+1)(S+3)

All roots are -4, -2, (-1)->lowest, -3

Since lowest root is pole so its RC.

Ϭ1 = 1, Ϭ2 = 3

Z(S) = K0 / S + K1 / S + Ϭ1 + K2 / S + Ϭ2

K0 = S(S+4)(S+2) / (S+1)(S+3) |S->0 = 0

K∞ = (1 + 6/S + 8/S2 / 1 + 4/S + 3/S2 )S->∞

K∞ = 1 =>  R∞ =1

K1 = 3/2 =>  R1 = 2/3  => C1 = 2/3

K2 = (S+4)(S+2) / (S+1)(S+3)(S+3) |S = -3

K2 = 1 / 2 => C2 = 2, R2 = 1/2

Q7) Realise using foster form (2), Y(S) = S2 + 6S + 8 / S2 + 4S + 3

A7)

Above function is RL admittance as lowest frequency is pole.

Y(S) = (S+4)(S+2) / (S+1)(S+3)

K0 = S(S+4)(S+2) / (S+1)(S+3) |S->0 = 0 , L0 = ∞

K1 = (S+4)(S+2) / (S+1)(S+3)(S+1)|S = -1

K1 = 3 / 2

L1 = 2 / 3, R1 = 2 / 3 (Ϭ1 / K1)

K2 = (S+4)(S+2) / (S+1)(S+3)(S+3) |S = -3

= 1 / 2, L2 = 2, R2 = Ϭ2 / K2 = 3 / ½ = 6

K∞ =  (S+4)(S+2) / (S+1)(S+3)|S -> ∞

= (1 + 4 / S)(1 + 2 / S) / (1 + 1 / S)(1 + 3 / S )|S -> ∞

K∞ = 1, R∞ = 1 / K∞ = 1

Q8) Realise the following function Y(S) = S2 + 4S + 3 / S2 + 6S + 8

A8)

Lowest critical frequency is zero.  Ϭ1 = +4, Ϭ2 = +2

Y(S) = (S+1)(S+3) / S(S+4)(S+2)

K0 = 3 / 8, R0 = 8 / 3

K∞ = (S+1)(S+3) / S(S+4)(S+2)|S->∞

= (1 + 1/S)(1 + 3/S) / S(1 + 4/S)(1 + 2/S)|S->∞

K∞ = 0, C∞ = 0

K1 = (S+1)(S+3)(S+4) / S(S+4)(S+2)|S = - 4

K1 = 3/8, R1 = 8/3

C1 = K1/Ϭ1 = 3/8 x ¼ = 3/32

K2 = (S+1)(S+3) / S(S+4)(S+2)|S = -2   = 1/4

K2 = 1/4, R2 = 4

C2 = K2/ Ϭ2 = 1/8

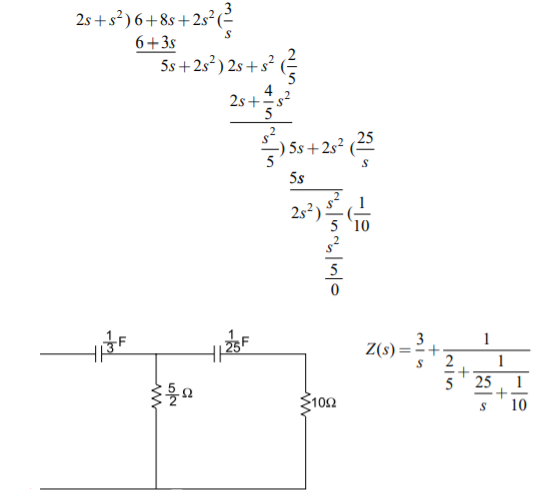
Q9) Synthesize the given transfer function using Cauer 1 Z(S) = S2 + 4S + 3 / S2 + 2S?

A9)

Q10) For the function Z(S) = S2 + 4S + 3 / S2 + 2S synthesize using cauer-II?

A10)

Arrange numerator and denominator in ascending order.

Z(S) = 3 + 4S + S2 / 2S + S2

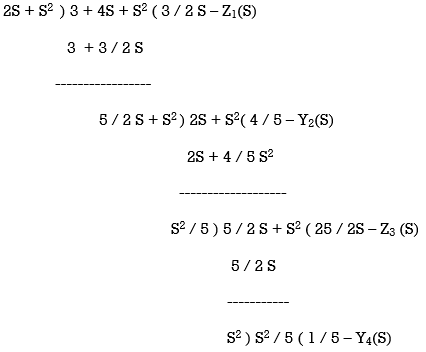
Z1(S) = 3 / 2S = 1 / CS ; C = 2 / 3

Y2(S) – 4 / 5 = 1 / Q ; R = 5 / 4

Z3(S) = 25 / 2S  ; C = 2 / 25

Y4(S) = 1 / 5 ; R = 5

Q11) The driving point impedance of a one-port reactive network is given by

Z(s)= 2s5+12s3+16s/s4+4s2+3. Determine first cauer form of the network?

A11) By taking continued fraction expansion, we get

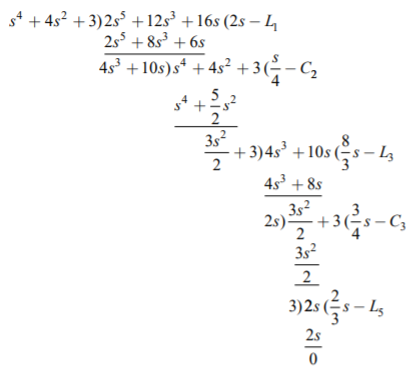
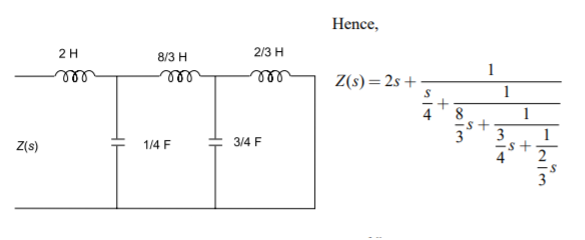
Q12) The driving point impedance of an LC network is given by Z(s)= s4 +4s2+ 3/(s3+2s) Determine the second Cauer form of the network.

A13) To obtain the second Cauer form, we have to arrange the numerator and the denominator of given Z(s) in ascending powers of s before starting the continued fraction expansion. By taking continued fraction expansion, we get

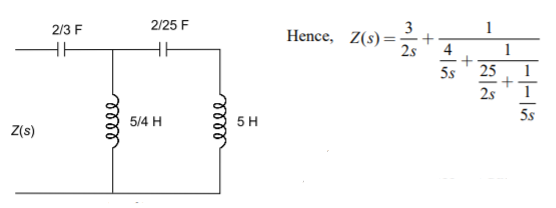
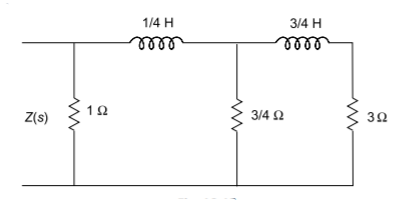
Q13) For the given function find cauer form I, Z(s)=(s+4) (s+8)/(s+2) (s+6)?

A13) To find out the first Cauer form, let us take the continued fraction expansion of Z(s)

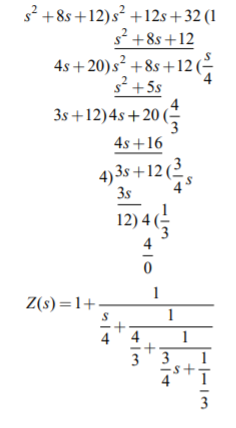
Q14) For the transfer function Z(s) = 2s2+8s+16/s2+8s+12. Realise with cauer form II?

A14) To find out the second Cauer network, we have to write the impedance function in ascending powers. By taking the continued fraction expansion of Z(s), we have

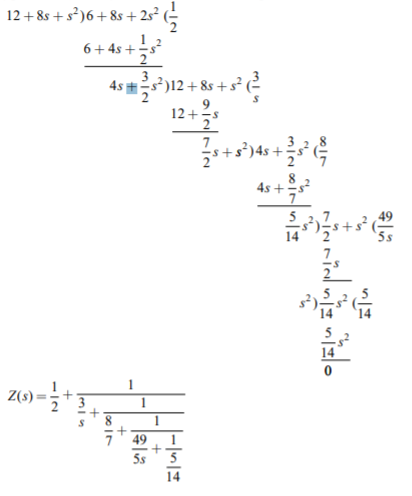
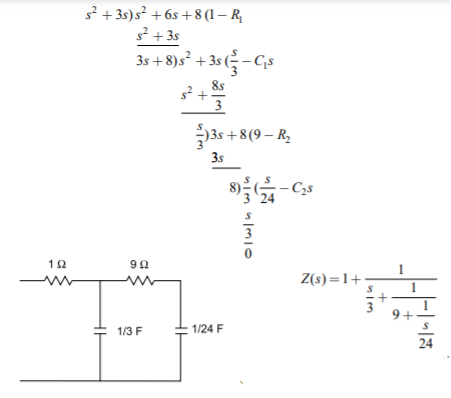
Q15) Consider a function Z(s) = (s+2)(s+4)/s(s+3). Find the first cauer form for network?

A15) To find the first Cauer form, we take the continued fraction expansion by the divide, invert, divide procedure as follows.

Q16) Obtain second cauer form for the function Z(s) = (s+2) (s+4)/s(s+3).

A16) The second Cauer network can be obtained by arranging the numerator and denominator polynomials of Z(s) in ascending powers of s. The continued fraction expansion is

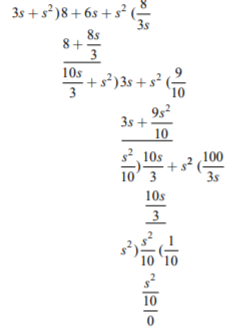
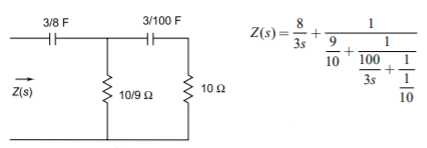
Q17) Find the two Foster realisations of the given function. Z(s) = 2s3+8s/s2+1?

A17) For the first Foster network, we expand Z(s) into partial fractions

Z(s)= 2s+[6s/s2+1)]

Z(s)= 2s+[3/s+j] +[3/s-j]

L2=6

C2=1/6

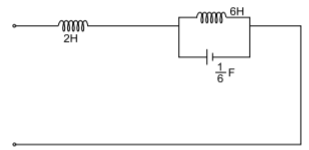
Second Foster network can be obtained by taking admittance function

Y(s)= s2+1/2s(s+4)

Solving by partial fraction we finally have

Y(s)= [1/8s]+[3/16(s+2j)]+[ 3/16(s-2j)]

L0=8H

L1=8/3H

C1=3/32F

The second Foster network with elemental values is shown

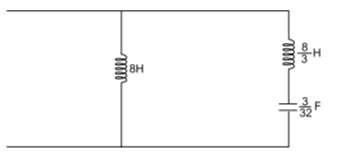
Q18) Find the two Foster realisations of the given function. Z(s)=3(s2+1) (s2+16)/s(s2+9).

A18) For the First Foster network, we expand Z(s) into partial fractions

Z(s)=3s+[24(s2+2)/s(s2+9)]

By partial fraction we have

Z(s)= 3s+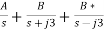

On solving we get

A=16/3

B=28/3=B*

Z(s)= 3s+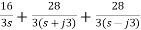

Then the values will be

C0= 1/A=3/16F

C2=1/2B=3/56F

L2=2B/wn2 = 56/27

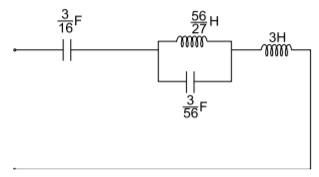
This is the Foster Form I

The Second form of Foster will be

Y(s)= s(s2+9)/s(s2+1) (s2+16)

Solving by partial fraction method

Y(s)=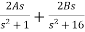

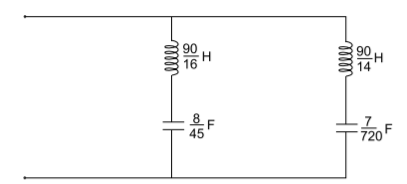
L1=1/2A=90/16H

C1=2A/ wn2 =8/45 F

L2=1/2B=90/14H

C2=2B/ w12=7/720F

The second Foster network with elemental values is shown in Fig.

Q19) Find the second cauer network of the given function. Z(s)= s4+6s2+4/s3+2s?

A19) The second cauer network can be realised by arranging the numerator and denominator polynomials of Z(s) in ascending power of s and taking continued fraction expansion, we get

Q20) Find the first and second Cauer forms of the function. Z(s)=2s2+8s+6/s2+2s

A20) The first cauer network can be realised by taking continued fraction expansion

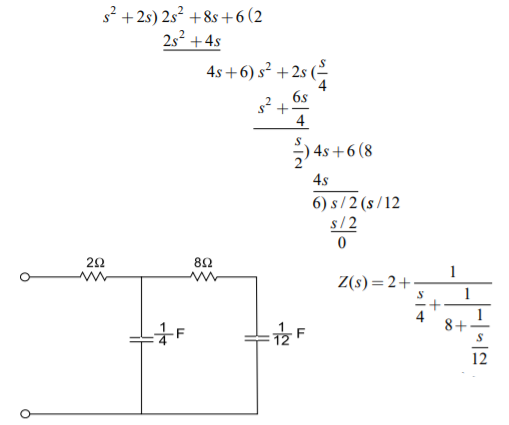
The second Cauer network can be realised by arranging the numerator and denominator polynomials of Z(s) in ascending power of s and taking continued fraction expansion, we get