Unit - 1
Harmonic Oscillation
Q1) Define Simple Harmonic Motion? Explain Damped and forced simple harmonic oscillator with examples?
A1) Simple harmonic motion is defined as a periodic motion of a point along a straight line, such that its acceleration is always towards a fixed point in that line and is proportional to its distance from that point.
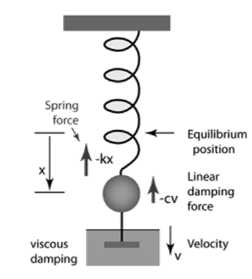
When the motion of an oscillator decreases due to an external force, the oscillator and its wave are damped.
These periodic motions of slowly decreasing amplitude are damped simple harmonic motion.
In the damped simple harmonic motion, the energy of the oscillator dissipates limitlessly. But for a small damping, the oscillations remain about periodic. The forces which scatter the energy are typically frictional forces.
The Newton's IInd Law of motion equation is
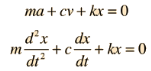
This is in the form of a homogeneous second order differential equation and has a explanation of the form
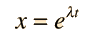
Replacing this form gives a secondary equation for λ
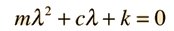
The roots of the quadratic secondary equation are
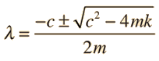
The three resultant cases for the damped oscillator are

Q2) Explain Damped Harmonic Oscillator?
A2) We have seen that the total energy of a harmonic oscillator remains constant. Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). Simple harmonic motions which persist indefinitely without loss of amplitude are called free or undamped.
However, observation of the free oscillations of a real physical system reveals that the energy of the oscillator gradually decreases with time and the oscillator eventually comes to rest. For example, the amplitude of a pendulum oscillating in the air decreases with time and it ultimately stops. The vibrations of a tuning fork die away with the passage of time. This happens because, in actual physical systems, friction (or damping) is always present. Friction resists motion.
The presence of resistance to motion implies that frictional or damping force acts on the system. The damping force acts in opposition to the motion, doing negative work on the system, leading to a dissipation of energy. When a body moves through a medium such as air, water, etc. its energy is dissipated due to friction and appears as heat either in the body itself or in the surrounding medium or both.
There is another mechanism by which an oscillator loses energy. The energy of an oscillator may decrease not only due to friction in the system but also due to radiation. The oscillating body imparts periodic motion to the particles of the medium in which it oscillates, thus producing waves. For example, a tuning fork produces sound waves in the medium which results in a decrease in its energy.
All sounding bodies are subject to dissipative forces, or otherwise, there would be no loss of energy by the body and consequently, no emission of sound energy could occur. Thus, sound waves are produced by radiation from mechanical oscillatory systems. The electromagnetic waves are produced by radiations from oscillating electric and magnetic fields.
The effect of radiation by an oscillating system and of the friction present in the system is that the amplitude of oscillations gradually diminishes with time. The reduction in amplitude (or energy) of an oscillator is called damping and the oscillation are said to be damped.
When the energy of a oscillating system is gradually dissipated by friction and other resistances, the oscillations are said to be damped. The oscillations gradually reduce or change in frequency or intensity or cease and the system rests in its equilibrium position.
Q3) Explain Damped Oscillations?
A3) Damped oscillations refer to oscillations where the oscillating object loses its energy to the surroundings.
Damping, in physics, restraining of vibratory motion, such as mechanical oscillations, noise, and alternating electric currents, by dissipation of energy. Unless a child keeps pumping a swing, its motion dies down because of damping. Shock absorbers in automobiles and carpet pads are examples of damping devices.
A system may be so damped that it cannot oscillate. Critical damping just prevents oscillation or is just sufficient to allow the object to return to its rest position in the shortest period of time.
There are many types of mechanical damping. Friction, also called in this context dry, or Coulomb, damping, arises chiefly from the electrostatic forces of attraction between the sliding surfaces and converts mechanical energy of motion, or kinetic energy, into heat. The motion of a oscillating body is also checked by its friction with the gas or liquid through which it moves.
Q4) Explain the sign of radicand of damped oscillations?
A4) In real systems, there is always a resistance or friction, which leads to a gradual damping of the oscillations. In many cases, the resistance force (denoted by FC) is proportional to the velocity of the body, that is
FC=−cx′.
Then, taking into account the force of resistance, the differential equation for the “mass-spring” system is written as
Mx′′+cx′+kx=0, ⇒ x′′+  x′+
x′+ x=0
x=0
We introduce the following notations:  =2β,
=2β,  =
= 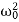 . Here ω0 is the natural frequency of the undamped oscillator (previously, we denoted it as ω), β is the damping coefficient. In the new notations, the differential equation looks like
. Here ω0 is the natural frequency of the undamped oscillator (previously, we denoted it as ω), β is the damping coefficient. In the new notations, the differential equation looks like
x′′+2βx′+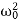 x=0.
x=0.
We will seek the solution of this equation as a function
x(t)=Aeλt.
The derivatives are given by
x′(t)=Aλeλt, x′′(t)=Aλ2eλt.
Substituting this into the differential equation, we obtain the algebraic characteristic equation:
Aλ2eλt+2βAλeλt+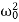 Aeλt=0,
Aeλt=0,
⇒λ2+2βλ+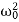 =0.
=0.
The roots of this equation are
D=4β2−4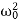 ,
,
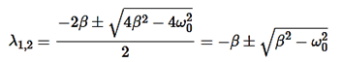
Q5) Explain Overdamping or Heavy damping?
A5) When resistance to motion is very strong, the system is said to be heavily damped. Can you name a heavily damped system of practical interest? Springs joining wagons of a train constitute the most important heavily damped system. In your physics laboratory, vibrations of a pendulum in a viscous medium such as thick oil and motion of the coil of a dead-beat galvanometer are heavily damped systems.
In this case (the case of strong damping), the radicand is positive: β2>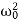 . The roots of the characteristic equation are real and negative. The general solution of the differential equation has the form
. The roots of the characteristic equation are real and negative. The general solution of the differential equation has the form
x(t)=C1eλ1t+C2eλ2t,
Where the coefficients C1, C2, as usual, depend on the initial conditions.
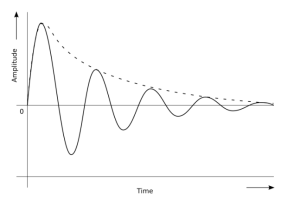
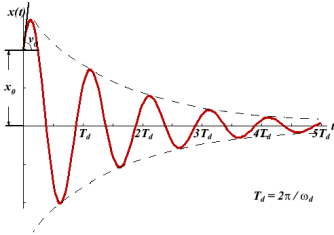
It follows from this expression that there are no oscillations and the system returns to equilibrium exponentially, i.e. a periodically as shown below:
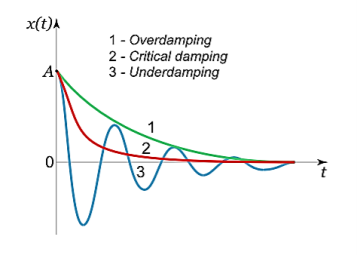
Damping Graph
Q6) Explain Critical Damping?
A6) We may have observed that on hitting an isolated road bump, a car bounces up and down and the occupants feel uncomfortable. To minimise this discomfort, the bouncing caused by the road bumps must be damped very rapidly and the automobile is restored to equilibrium quickly. For this we use critically damped shock absorbers. Critical damping is also useful in recording instruments such as a galvanometer (pointer type as well as suspended coil type) which experience sudden impulses. We require the pointer to move to the correct position in minimum time and stay there without executing oscillations. Similarly, a ballistic galvanometer coil is required to return to zero displacement immediately.
In the limiting case when β=ω0, the roots of the characteristic equation are real and coincide:
λ1=λ2=−β=−ω0.
Here the solution is given by the formula
x(t)=(C1t+C2)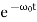
In this mode, the value of x(t) may even increase at the beginning of the process because of the linear factor C1t+C2. But in the end the deflection x(t) decreases rapidly due to the exponential decay with a characteristic time τ=2π/ω0.
Note that in this critical mode the relaxation occurs faster than in the case of the aperiodic damping (Case 1). Indeed, in this mode the relaxation time will be determined by the smaller (in absolute value) root λ1, and will be given by the formula
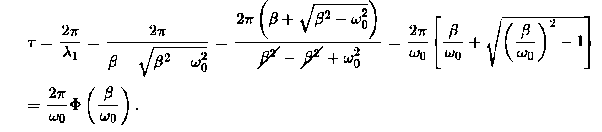
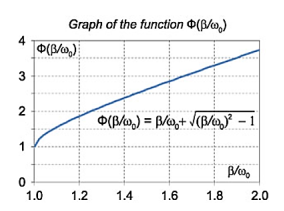
The function Φ(β/ω0) included in this expression is monotonically increasing. It is always greater than or equal to 1, as shown in the figure.
In the critical case (Case 2) the ratio βω0 is 1, and βω0>1 in the case of the aperiodic damping (Case 1). Therefore, for the aperiodic damping mode, we can write
τ=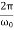 Φ(
Φ(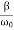 ) >
) > 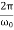
Thus, the critical damping mode provides the fastest possible return of the system to equilibrium. This is often used, for example, in door closing mechanisms.
Q7) Explain Underdamping or Light damping?
A7) Here the roots of the characteristic equation are complex conjugate:
λ1,2 =−β±i√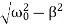
The general solution of the differential equation is oscillatory in nature and can be written as
x(t)=e−βt[C1cos(ω1t)+C2sin(ω1t)]
Where the oscillation frequency ω1 is equal to
ω1= 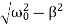
The resulting formula can be written in a somewhat different form:
x(t)=Ae−βtcos(ω1t+φ0),
Where φ0 is the initial phase of the oscillations and Acosφ0 is the initial amplitude of the oscillations. We see that classical damped oscillations occur in this mode. Here the oscillation frequency ω1 is less than the harmonic frequency ω0, and the oscillation amplitude decreases exponentially with e−βt.
Q8) Explain Amplitude in a damped Harmonic oscillator?
A8) If a frictional force (damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coefficient, the system can:
- Oscillate with a frequency lower than in the undamped case, and an amplitude decreasing with time (underdamped oscillator).
- Decay to the equilibrium position, without oscillations (overdamped oscillator).
The boundary solution between an underdamped oscillator and an overdamped oscillator occurs at a particular value of the friction coefficient and is called critically damped.
Q9) Explain Energy decay in a damped harmonic oscillator?
A9) We know that in the presence of damping the amplitude of oscillation decreases with the passage of time. This means that energy is dissipated in overcoming resistance to motion. We know that, the total energy of a harmonic oscillator is made up of kinetic and potential components. We can still use the same definition and write
E(t) = K.E. + P.E.
=  m (
m (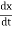 )2+
)2+  kx2
kx2
Where (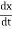 ) denotes instantaneous velocity. For a weakly damped harmonic oscillator, the instantaneous displacement is given by
) denotes instantaneous velocity. For a weakly damped harmonic oscillator, the instantaneous displacement is given by
x(t) = a0 exp(-bt) cos (ωdt +ϕ)
By differentiating it with respect to time, we get instantaneous velocity:
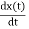 = v = a0 exp(-bt) [bcos (ωdt +ϕ) +ωd sin (ωdt +ϕ)]
= v = a0 exp(-bt) [bcos (ωdt +ϕ) +ωd sin (ωdt +ϕ)]
Hence, kinetic energy of the oscillator is
K.E. =  m (
m (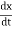 )2 =
)2 =  m a02 exp(-2bt) [bcos (ωdt +ϕ) +ωd sin (ωdt +ϕ)]2
m a02 exp(-2bt) [bcos (ωdt +ϕ) +ωd sin (ωdt +ϕ)]2
=  m a02 exp(-2bt) [b2cos2 (ωdt +ϕ) +ω2d sin2 (ωdt +ϕ) + b ωd 2sin (ωdt +ϕ)]
m a02 exp(-2bt) [b2cos2 (ωdt +ϕ) +ω2d sin2 (ωdt +ϕ) + b ωd 2sin (ωdt +ϕ)]
Similarly, the potential energy of the oscillator is
U =P.E.=  kx2 =
kx2 = 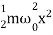
Since k = 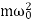
On substituting for x, we get
U = 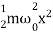 =
= 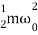 a02 exp(-2bt) [cos (ωdt +ϕ)]2
a02 exp(-2bt) [cos (ωdt +ϕ)]2
Hence, the total energy of the oscillator at any time t is given by
E(t) =  m a02 exp(-2bt) [(b2+ ω2o) cos2 (ωdt +ϕ) +ω2d sin2 (ωdt +ϕ) + b ωd 2sin (ωdt +ϕ)]
m a02 exp(-2bt) [(b2+ ω2o) cos2 (ωdt +ϕ) +ω2d sin2 (ωdt +ϕ) + b ωd 2sin (ωdt +ϕ)]
When damping is small, the amplitude of oscillation does not change much over one oscillation. So we may take the factor exp (-2bt) as essentially constant.
Further, since < sin2 (ωdt +ϕ) > = < cos2 (ωdt +ϕ) > =  and <sin (ωdt +ϕ)> = 0, the energy of a weakly damped oscillator when averaged-over one cycle is given by
and <sin (ωdt +ϕ)> = 0, the energy of a weakly damped oscillator when averaged-over one cycle is given by
<E> = <  m a02 exp(-2bt) [(b2+ ω2o) cos2 (ωdt +ϕ) +ω2d sin2 (ωdt +ϕ) + b ωd 2sin (ωdt +ϕ)]>
m a02 exp(-2bt) [(b2+ ω2o) cos2 (ωdt +ϕ) +ω2d sin2 (ωdt +ϕ) + b ωd 2sin (ωdt +ϕ)]>
<E> =  m a02 exp(-2bt) [
m a02 exp(-2bt) [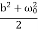 +
+ 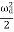 ]
]
<E> =  m a02
m a02 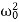 exp(-2bt)
exp(-2bt)
E0 = m a02
m a02 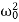 is the total energy of an undamped oscillator. Hence, we can write <E> = Eo exp (- 2bt)
is the total energy of an undamped oscillator. Hence, we can write <E> = Eo exp (- 2bt)
This shows that the average energy of a weakly damped oscillator decreases exponentially with time. This is illustrated in Figure 6. You will also observe that the rate of decay of energy depends on the value of b; larger the value of b, faster will be the decay.
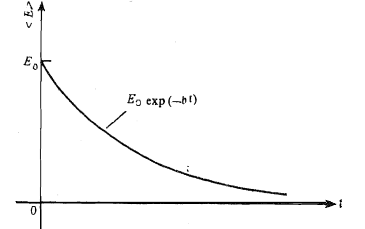
Q10) Explain Forced oscillation and resonance condition?
A10) We instead of permitting our system to vacillate in isolation we apply a "driving force". For example, in the case of the (vertical) mass on a spring the driving force might be useful by having an external force (F) move the maintenance of the spring up and down. In this case the equation of motion of the mass is given by,
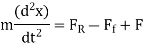 One common condition happens when the driving force itself oscillates, in which case we may write
One common condition happens when the driving force itself oscillates, in which case we may write
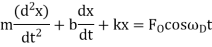
Where 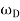 is the (angular) frequency of the driving force.
is the (angular) frequency of the driving force.
This equation has solutions of the form
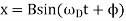
Where the amplitude of these oscillations, B, depends on the parameters of the motion, 
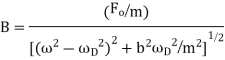
The amplitude, B, has a determined value when 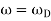 . This is called the resonance condition. Note that at resonance, B, can become very large if b is small. (In the diagram at right
. This is called the resonance condition. Note that at resonance, B, can become very large if b is small. (In the diagram at right  is the natural frequency of the oscillations,
is the natural frequency of the oscillations, 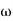 , in the above analysis). In designing physical systems, it is very important to find the system's natural frequencies of vibration and provide sufficient damping in case of resonance. This clearly did not occur in the design of the Tacoma Narrows Bridge (Tacoma Narrows Newsreel) in 1940.
, in the above analysis). In designing physical systems, it is very important to find the system's natural frequencies of vibration and provide sufficient damping in case of resonance. This clearly did not occur in the design of the Tacoma Narrows Bridge (Tacoma Narrows Newsreel) in 1940.
There are many physical and engineering systems where resonance is very important e.g., shock absorbers, earthquakes, loudspeakers, NMR, microwave ovens etc.