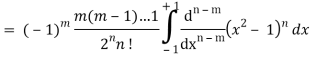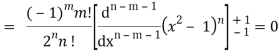Unit - 3

Higher order linear differential equations with constant and variable coefficients

Q1) Solve (4D² +4D -3)y = e2x 

A1)

Auxiliary equation is 4m² +4m – 3 = 0

We get, (2m+3) (2m – 1) = 0

m = -3/2, 1/2

Complementary function:  CF is A e-3x/2+ B e1 x/2

Now we will find particular integral,

P.I. = 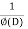f(x)

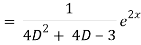
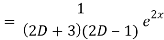
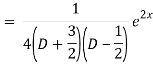
General solution is y = CF + PI

= A e-3x/2+ B e1 x/2 + 1/21 . e2x

Q2) Solve (D2 + 6D + 9) = 0

A2)

Its auxiliary equation is-

D2 + 6D + 9 = 0

(D + 3)2 = 0

Where-

D = -3, -3

Therefore, the complete solution is-

x = (c1 + c2t)e-3t

Q3) Find the P.I. Of (D + 2)(D – 1)2 y = e-2x + 2 sin h x

A3)

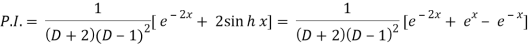
Now we will evaluate each term separately-

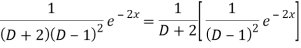
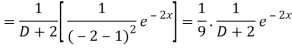
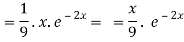
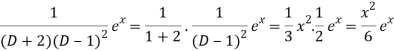
And

Therefore-

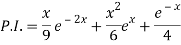
Q4) Solve (D – D’ – 2) (D – D’ – 3) z =

A4)

The C.F. Will be given by-

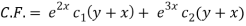
Particular integral-

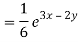
Therefore, the complete solution is-

z = C.F. + P.I. = e2x c1(y + x) + e3x c3(y+x) + 1/5 e3x – 2y

Q5) Find P.I. Of  (D2 – 2D + 4) y = ex cos x

A5)

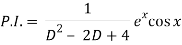
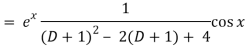
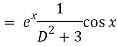
Put

D2 = - 12 = -1

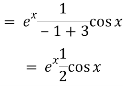
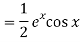
Q6) Solve (D2 + 4D + 4)y = 3 sin x + 4 cos x

A6)

Here first we will find the C.F.-

Its auxiliary equation will be-

D2 + 4D + 4 or (D + 2)2 = 0

Here we get-

D = -2, -2

C.F. = (c1 + c2x)e-2x

Now we will find P.I.-

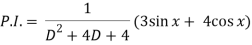
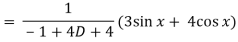
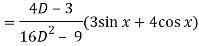
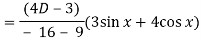
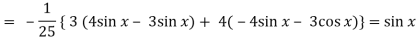
Now the complete solution is-

Complete solution = C.F. + P.I.

= (c1 + c2 x)e-2x + sin x

Q7) Solve-

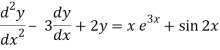
A7)

The given equation can be written as-

(D2 – 3D + 2) y = xe3x + sin 2x

Its auxiliary equation is-

D2 – 3D + 2 = 0 or (D – 2)(D – 1) = 0

We get-

D = 1, 2

So that the C.F. Will be-

C. F. = c1ex + c2e2x

Now we will find P.I.-

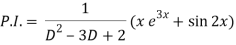
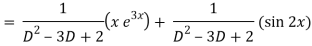
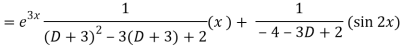
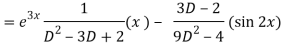
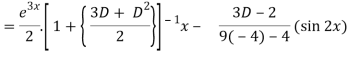
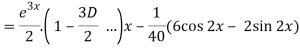
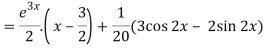
Therefore, the complete solution is-

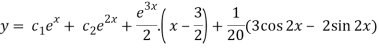
Q8) Solve the following simultaneous differential equations-

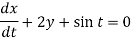
It is given that x = 0 and y = 1 when t = 0.

A8)

Given equations can be written as-

Dx + 2y = - sin t ………. (1)    and     -2x + Dy = cos t  ……… (2)

Eliminate x by multiplying (1) by 2 and (2) by D then add-

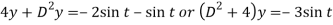
Here A.E =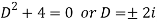

So that C.F. =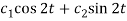

And P.I. =

So that- 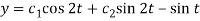   …………. (3)

And 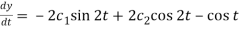  ………….. (4)

Substitute (3) in (2), we get-

2x = Dy – cos t =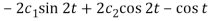

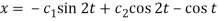  ………… (5)

When t = 0, x = 0, y = 1. (3) and (5) gives-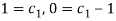 

Hence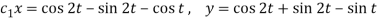

Q9) Solve the following DE by using variation of parameters-

A9)

We can write the given equation in symbolic form as-

(D2 + 4)y = tan 2x

To find CF-

It’s A.E. Is (D2 + 4) = 0   or  D = ± 2

So that CF is-   y = c1 cos 2x + c2 sin 2x   

To find PI-

Here y1 = cos 2x, y2 = sin 2x   and X = tan 2x

Now   W =

Thus PI = -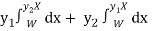

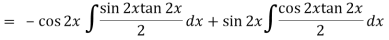
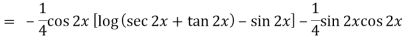
= - ¼ cos 2x log ( sec 2x + tan 2x)

So that the complete solution is-

y = c1 cos 2x + c2  sin 2x – ¼ cos 2x log (sec 2x + tan 2x)

Q10) Solve the following by using the method of variation of parameters.

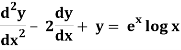
A10)

This can be written as-

(D2 – 2D + 1)y = ex log x

C.F.-

Auxiliary equation is- D2 – 2D + 1= 0 or (D – 1)2 so that D = 1, 1

So that the C.F. Will be- (c1 + c2x)ex

P.I.-

Here y1 = ex , y2 = xex  and  X = ex log x

Now      W =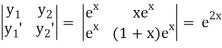  

Thus PI = -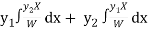          

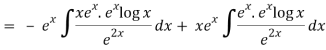
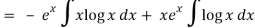
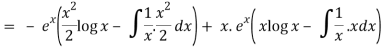
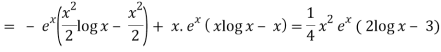
So that the complete solution is-

y = (c1 + c2x)ex + ¼ x2 ex(2 log x – 3)

Q11)

A11)

Putting,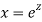

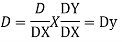
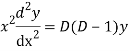
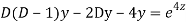
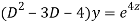
AE is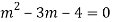

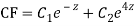
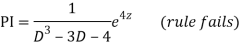
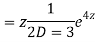
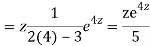
CS = CF + PI

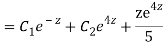
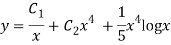
Q12) Solve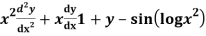

A12)

Let,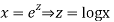

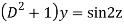
AE is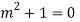

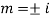
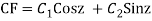
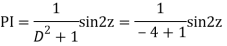
y= CF + PI

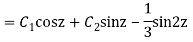
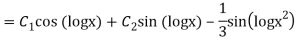
Q13) Solve

A13)

As we see that this is Legendre’s linear equation.

Now put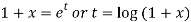

So that-

And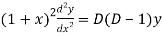

Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t

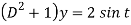
Its auxiliary equation is-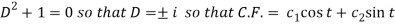

And particular integral-

               P.I. =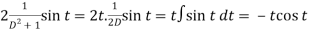

Note -

Hence the solution is -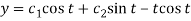

Q14) Solve the following simultaneous differential equations-

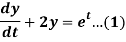
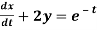....(2)

A14)

Consider the given equations

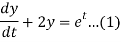
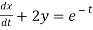....(2)

Consider eq(1),(2)

Dx+2y = et....(1)

Dx +2x =e-t....(2)

Eliminating ‘x’ from both the equations we get,

12 2Dx + 2y = 2et

D 2Dx +D2y = e-t

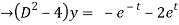
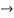y = Ae2t + Be-2t +

Q15) Solve the following simultaneous differential equations-

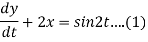
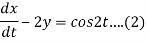
Given that x(0)=1  and y(0)= 0

A15)

Consider the given equations,

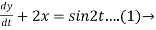Dy +2x = sin2t

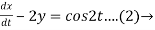Dx -2y = cos2t

By solving the above equations, we get,

(D2 +4)Y =0

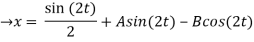
X(0) = 1, y(0) = 0

A =0, B=-1

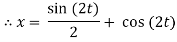
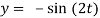
Q16) Solve                      

 (D2 + 8D + 15)y = 0

A16)

Given,  (D2 + 8D + 15)y = 0

Here Auxiliary equation is

m2 – 8m + 15 = 9

m2 – 3m – 5m + 15 = 0

m(m – 3) – 5(m -3) = 0

(m – 3) (m – 5) = 0

m = 3, 5

y = C1e3x + C2 e5x

Q17) Solve: (D2 + 4)y = Cos 2x

A17)

Auxiliary equation are m2 + 4 = 0

CF = A Cos 2x + B Sin 2x

PI =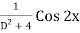

Put , D2 = - a2 = -22 = -4

PI =

PI = x

= x/4 Sin 2x

CS = CF + PR

= A Cos 2x + B Sin 2x + x/4 Sin 2x

Q18) Prove that-

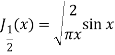
A18)

As we know that-

Jn(x) =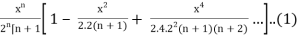

Now put n = 1/2 in equation (1), then we get-

J1/2(x) =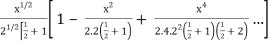

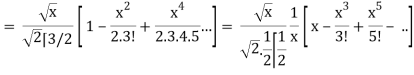
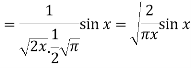
Hence proved.

Q19) Prove that-

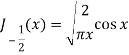
A19)

Put n = -1/2 in equation (1) of the above question, we get-

J1/2(x) =

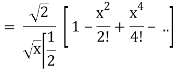
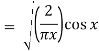
Q20) Show that-

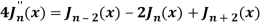
By using recurrence relation.

A20)

We know that-

The recurrence formula-

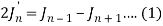
On differentiating, we get-

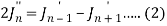
Now replace n by n -1 and n by n+1 in (1), we have-

2 J’n – 1 = Jn – 2 – Jn         or         J’n – 1 = ½  Jn – 2 – ½ Jn

2 J’n+1 = Jn – Jn+2           or         J’n+1 = ½ Jn – ½ Jn+2

Put the values of 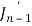and 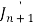from the above equations in (2), we get-

2J’’n = ½ [ Jn-2 – Jn] – ½ [ Jn – Jn + 2]

4J’’n = Jn – 2 – Jn – Jn + Jn+2

4J’’n = Jn – 2 – 2 Jn + Jn+2

Q21) Prove that-

A21)

We know that- from recurrence formula

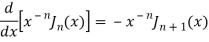
On integrating we get-

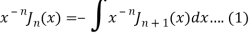
On taking n = 2 in (1), we get-

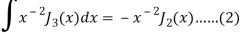
Again-

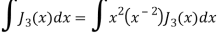
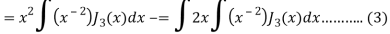
Put the value of 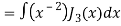from equation (2) and (3), we get-

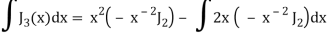
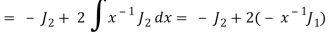
By equation (1), when n = 1

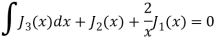
Q22) Express 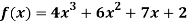in terms of Legendre polynomials.

A22)

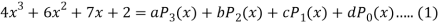
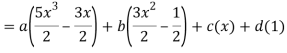
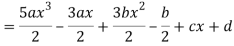
By equating the coefficients of like powers of x, we get-

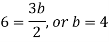
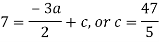
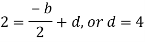
Put these values in equation (1), we get-

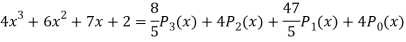
Q23) Let 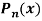be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-

A23)

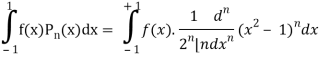
We know that-

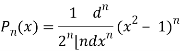
On integrating by parts, we get-

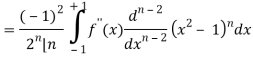
Now integrate (n – 2) times by parts, we get-

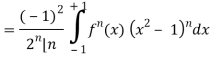
Q24) Show that-

P2n(0) = (-1)n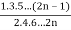

A24)

We know that

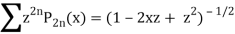
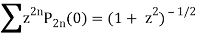
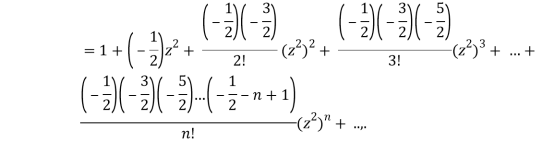
Equating the coefficients of 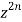both sides, we have-

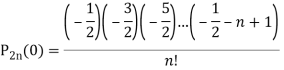
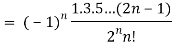
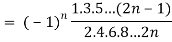
Q25) Prove that-

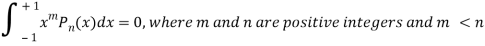
A25)

By using Rodrigue formula for Legendre function.

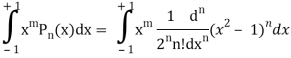
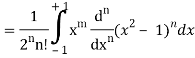
On integrating by parts, we get-

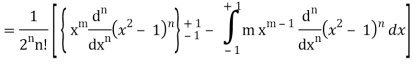
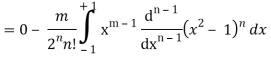
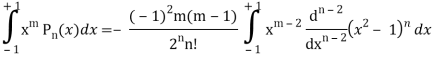
Now integrating m – 2 times, we get-

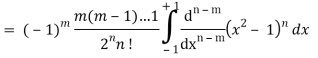
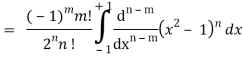
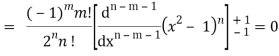
Unit - 3

Higher order linear differential equations with constant and variable coefficients

Q1) Solve (4D² +4D -3)y = e2x 

A1)

Auxiliary equation is 4m² +4m – 3 = 0

We get, (2m+3) (2m – 1) = 0

m = -3/2, 1/2

Complementary function:  CF is A e-3x/2+ B e1 x/2

Now we will find particular integral,

P.I. = f(x)

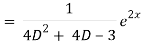
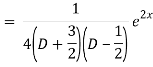
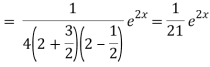
General solution is y = CF + PI

= A e-3x/2+ B e1 x/2 + 1/21 . e2x

Q2) Solve (D2 + 6D + 9) = 0

A2)

Its auxiliary equation is-

D2 + 6D + 9 = 0

(D + 3)2 = 0

Where-

D = -3, -3

Therefore, the complete solution is-

x = (c1 + c2t)e-3t

Q3) Find the P.I. Of (D + 2)(D – 1)2 y = e-2x + 2 sin h x

A3)

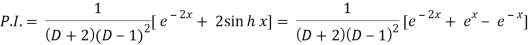
Now we will evaluate each term separately-

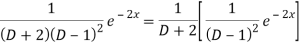
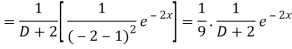
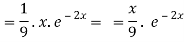
And

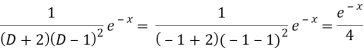
Therefore-

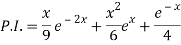
Q4) Solve (D – D’ – 2) (D – D’ – 3) z =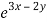

A4)

The C.F. Will be given by-

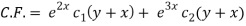
Particular integral-

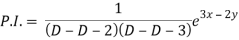
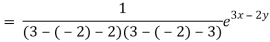
Therefore, the complete solution is-

z = C.F. + P.I. = e2x c1(y + x) + e3x c3(y+x) + 1/5 e3x – 2y

Q5) Find P.I. Of  (D2 – 2D + 4) y = ex cos x

A5)

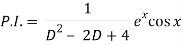
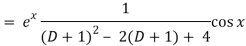
Put

D2 = - 12 = -1

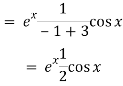
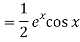
Q6) Solve (D2 + 4D + 4)y = 3 sin x + 4 cos x

A6)

Here first we will find the C.F.-

Its auxiliary equation will be-

D2 + 4D + 4 or (D + 2)2 = 0

Here we get-

D = -2, -2

C.F. = (c1 + c2x)e-2x

Now we will find P.I.-

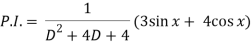
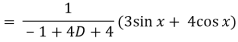
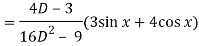
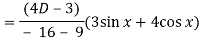
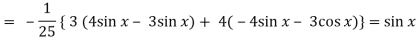
Now the complete solution is-

Complete solution = C.F. + P.I.

= (c1 + c2 x)e-2x + sin x

Q7) Solve-

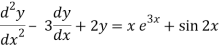
A7)

The given equation can be written as-

(D2 – 3D + 2) y = xe3x + sin 2x

Its auxiliary equation is-

D2 – 3D + 2 = 0 or (D – 2)(D – 1) = 0

We get-

D = 1, 2

So that the C.F. Will be-

C. F. = c1ex + c2e2x

Now we will find P.I.-

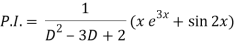
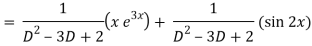
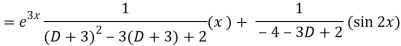
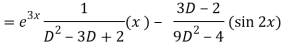
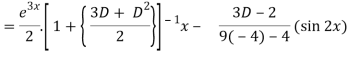
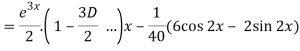
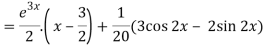
Therefore, the complete solution is-

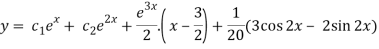
Q8) Solve the following simultaneous differential equations-

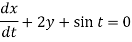
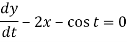
It is given that x = 0 and y = 1 when t = 0.

A8)

Given equations can be written as-

Dx + 2y = - sin t ………. (1)    and     -2x + Dy = cos t  ……… (2)

Eliminate x by multiplying (1) by 2 and (2) by D then add-

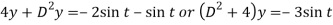
Here A.E =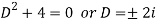

So that C.F. =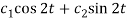

And P.I. =

So that- 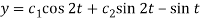   …………. (3)

And 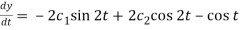  ………….. (4)

Substitute (3) in (2), we get-

2x = Dy – cos t =

  ………… (5)

When t = 0, x = 0, y = 1. (3) and (5) gives- 

Hence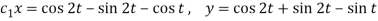

Q9) Solve the following DE by using variation of parameters-

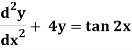
A9)

We can write the given equation in symbolic form as-

(D2 + 4)y = tan 2x

To find CF-

It’s A.E. Is (D2 + 4) = 0   or  D = ± 2

So that CF is-   y = c1 cos 2x + c2 sin 2x   

To find PI-

Here y1 = cos 2x, y2 = sin 2x   and X = tan 2x

Now   W =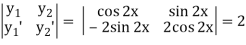

Thus PI = -

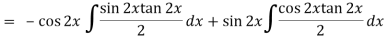
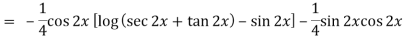
= - ¼ cos 2x log ( sec 2x + tan 2x)

So that the complete solution is-

y = c1 cos 2x + c2  sin 2x – ¼ cos 2x log (sec 2x + tan 2x)

Q10) Solve the following by using the method of variation of parameters.

A10)

This can be written as-

(D2 – 2D + 1)y = ex log x

C.F.-

Auxiliary equation is- D2 – 2D + 1= 0 or (D – 1)2 so that D = 1, 1

So that the C.F. Will be- (c1 + c2x)ex

P.I.-

Here y1 = ex , y2 = xex  and  X = ex log x

Now      W =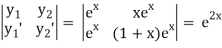  

Thus PI = -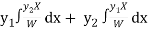          

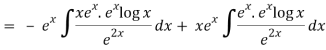
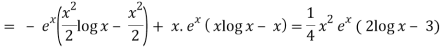
So that the complete solution is-

y = (c1 + c2x)ex + ¼ x2 ex(2 log x – 3)

Q11)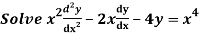

A11)

Putting,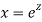

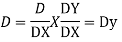
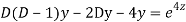
AE is

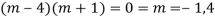
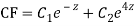
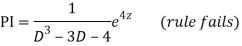
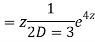
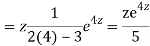
CS = CF + PI

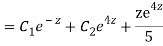
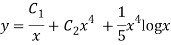
Q12) Solve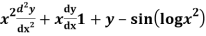

A12)

Let,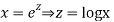

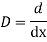
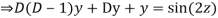
AE is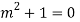

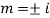
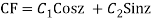
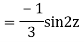
y= CF + PI

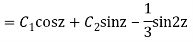
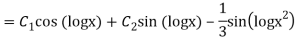
Q13) Solve

A13)

As we see that this is Legendre’s linear equation.

Now put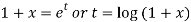

So that-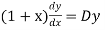

And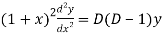

Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t

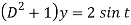
Its auxiliary equation is-

And particular integral-

               P.I. =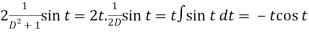

Note -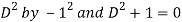

Hence the solution is -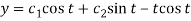

Q14) Solve the following simultaneous differential equations-

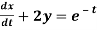....(2)

A14)

Consider the given equations

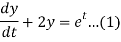
....(2)

Consider eq(1),(2)

Dx+2y = et....(1)

Dx +2x =e-t....(2)

Eliminating ‘x’ from both the equations we get,

12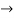 2Dx + 2y = 2et

D 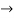2Dx +D2y = e-t

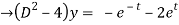
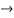y = Ae2t + Be-2t +

Q15) Solve the following simultaneous differential equations-

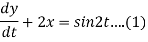
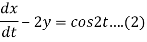
Given that x(0)=1  and y(0)= 0

A15)

Consider the given equations,

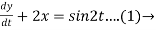Dy +2x = sin2t

Dx -2y = cos2t

By solving the above equations, we get,

(D2 +4)Y =0

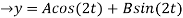
X(0) = 1, y(0) = 0

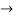A =0, B=-1

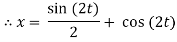
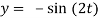
Q16) Solve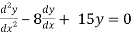                      

 (D2 + 8D + 15)y = 0

A16)

Given,  (D2 + 8D + 15)y = 0

Here Auxiliary equation is

m2 – 8m + 15 = 9

m2 – 3m – 5m + 15 = 0

m(m – 3) – 5(m -3) = 0

(m – 3) (m – 5) = 0

m = 3, 5

y = C1e3x + C2 e5x

Q17) Solve: (D2 + 4)y = Cos 2x

A17)

Auxiliary equation are m2 + 4 = 0

CF = A Cos 2x + B Sin 2x

PI =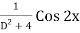

Put , D2 = - a2 = -22 = -4

PI =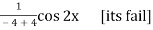

PI = x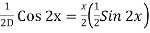

= x/4 Sin 2x

CS = CF + PR

= A Cos 2x + B Sin 2x + x/4 Sin 2x

Q18) Prove that-

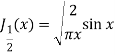
A18)

As we know that-

Jn(x) =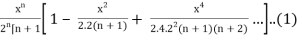

Now put n = 1/2 in equation (1), then we get-

J1/2(x) =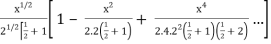

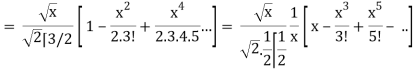
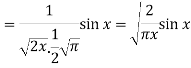
Hence proved.

Q19) Prove that-

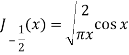
A19)

Put n = -1/2 in equation (1) of the above question, we get-

J1/2(x) =

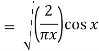
Q20) Show that-

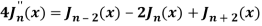
By using recurrence relation.

A20)

We know that-

The recurrence formula-

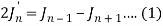
On differentiating, we get-

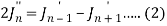
Now replace n by n -1 and n by n+1 in (1), we have-

2 J’n – 1 = Jn – 2 – Jn         or         J’n – 1 = ½  Jn – 2 – ½ Jn

2 J’n+1 = Jn – Jn+2           or         J’n+1 = ½ Jn – ½ Jn+2

Put the values of and 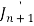from the above equations in (2), we get-

2J’’n = ½ [ Jn-2 – Jn] – ½ [ Jn – Jn + 2]

4J’’n = Jn – 2 – Jn – Jn + Jn+2

4J’’n = Jn – 2 – 2 Jn + Jn+2

Q21) Prove that-

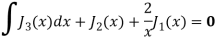
A21)

We know that- from recurrence formula

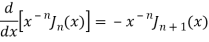
On integrating we get-

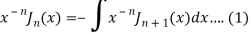
On taking n = 2 in (1), we get-

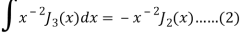
Again-

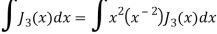
Put the value of 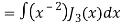from equation (2) and (3), we get-

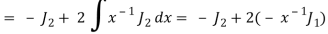
By equation (1), when n = 1

Q22) Express in terms of Legendre polynomials.

A22)

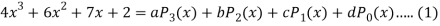
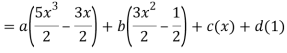
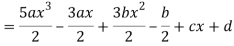
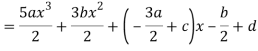
By equating the coefficients of like powers of x, we get-

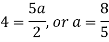
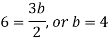
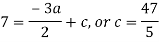
Put these values in equation (1), we get-

Q23) Let 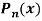be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-

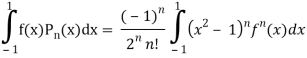
A23)

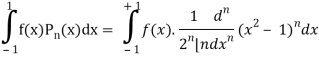
We know that-

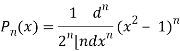
On integrating by parts, we get-

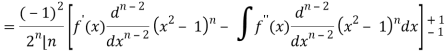
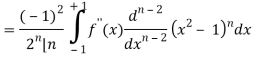
Now integrate (n – 2) times by parts, we get-

Q24) Show that-

P2n(0) = (-1)n

A24)

We know that

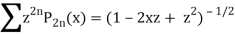
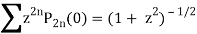
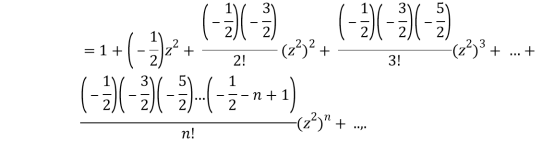
Equating the coefficients of 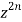both sides, we have-

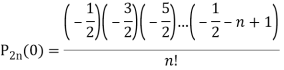
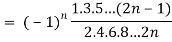
Q25) Prove that-

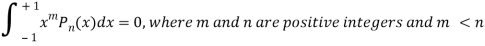
A25)

By using Rodrigue formula for Legendre function.

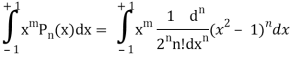
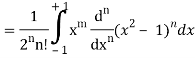
On integrating by parts, we get-

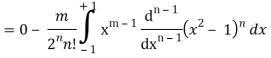
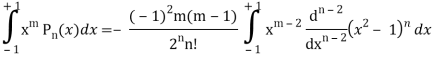
Now integrating m – 2 times, we get-

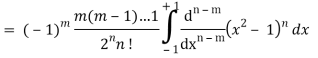
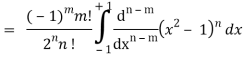
Unit - 3

Unit - 3

Unit - 3

Higher order linear differential equations with constant and variable coefficients

Q1) Solve (4D² +4D -3)y = e2x 

A1)

Auxiliary equation is 4m² +4m – 3 = 0

We get, (2m+3) (2m – 1) = 0

m = -3/2, 1/2

Complementary function:  CF is A e-3x/2+ B e1 x/2

Now we will find particular integral,

P.I. = 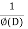f(x)

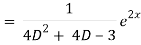
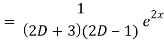
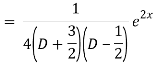
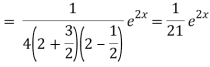
General solution is y = CF + PI

= A e-3x/2+ B e1 x/2 + 1/21 . e2x

Q2) Solve (D2 + 6D + 9) = 0

A2)

Its auxiliary equation is-

D2 + 6D + 9 = 0

(D + 3)2 = 0

Where-

D = -3, -3

Therefore, the complete solution is-

x = (c1 + c2t)e-3t

Q3) Find the P.I. Of (D + 2)(D – 1)2 y = e-2x + 2 sin h x

A3)

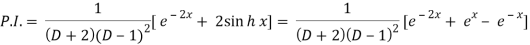
Now we will evaluate each term separately-

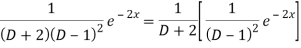
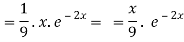
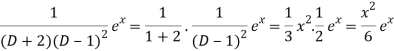
And

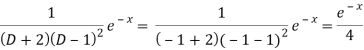
Therefore-

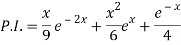
Q4) Solve (D – D’ – 2) (D – D’ – 3) z =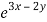

A4)

The C.F. Will be given by-

Particular integral-

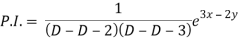
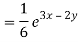
Therefore, the complete solution is-

z = C.F. + P.I. = e2x c1(y + x) + e3x c3(y+x) + 1/5 e3x – 2y

Q5) Find P.I. Of  (D2 – 2D + 4) y = ex cos x

A5)

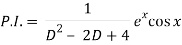
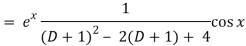
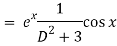
Put

D2 = - 12 = -1

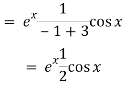
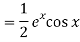
Q6) Solve (D2 + 4D + 4)y = 3 sin x + 4 cos x

A6)

Here first we will find the C.F.-

Its auxiliary equation will be-

D2 + 4D + 4 or (D + 2)2 = 0

Here we get-

D = -2, -2

C.F. = (c1 + c2x)e-2x

Now we will find P.I.-

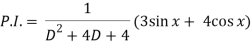
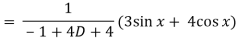
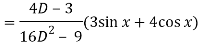
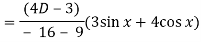
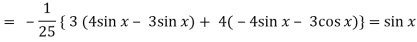
Now the complete solution is-

Complete solution = C.F. + P.I.

= (c1 + c2 x)e-2x + sin x

Q7) Solve-

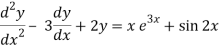
A7)

The given equation can be written as-

(D2 – 3D + 2) y = xe3x + sin 2x

Its auxiliary equation is-

D2 – 3D + 2 = 0 or (D – 2)(D – 1) = 0

We get-

D = 1, 2

So that the C.F. Will be-

C. F. = c1ex + c2e2x

Now we will find P.I.-

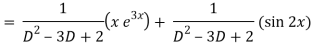
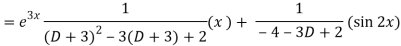
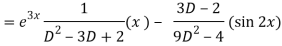
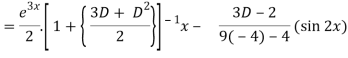
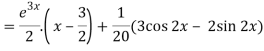
Therefore, the complete solution is-

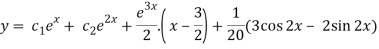
Q8) Solve the following simultaneous differential equations-

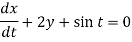
It is given that x = 0 and y = 1 when t = 0.

A8)

Given equations can be written as-

Dx + 2y = - sin t ………. (1)    and     -2x + Dy = cos t  ……… (2)

Eliminate x by multiplying (1) by 2 and (2) by D then add-

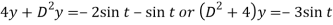
Here A.E =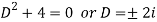

So that C.F. =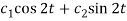

And P.I. =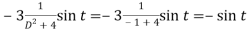

So that- 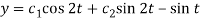   …………. (3)

And 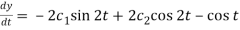  ………….. (4)

Substitute (3) in (2), we get-

2x = Dy – cos t =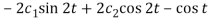

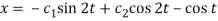  ………… (5)

When t = 0, x = 0, y = 1. (3) and (5) gives- 

Hence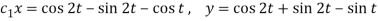

Q9) Solve the following DE by using variation of parameters-

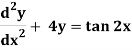
A9)

We can write the given equation in symbolic form as-

(D2 + 4)y = tan 2x

To find CF-

It’s A.E. Is (D2 + 4) = 0   or  D = ± 2

So that CF is-   y = c1 cos 2x + c2 sin 2x   

To find PI-

Here y1 = cos 2x, y2 = sin 2x   and X = tan 2x

Now   W =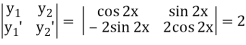

Thus PI = -

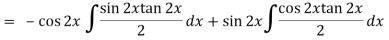
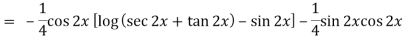
= - ¼ cos 2x log ( sec 2x + tan 2x)

So that the complete solution is-

y = c1 cos 2x + c2  sin 2x – ¼ cos 2x log (sec 2x + tan 2x)

Q10) Solve the following by using the method of variation of parameters.

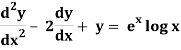
A10)

This can be written as-

(D2 – 2D + 1)y = ex log x

C.F.-

Auxiliary equation is- D2 – 2D + 1= 0 or (D – 1)2 so that D = 1, 1

So that the C.F. Will be- (c1 + c2x)ex

P.I.-

Here y1 = ex , y2 = xex  and  X = ex log x

Now      W =  

Thus PI = -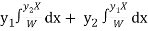          

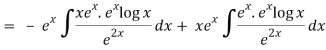
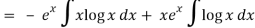
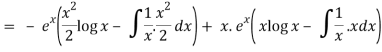
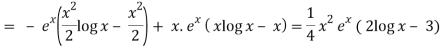
So that the complete solution is-

y = (c1 + c2x)ex + ¼ x2 ex(2 log x – 3)

Q11)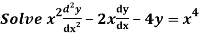

A11)

Putting,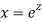

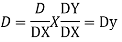
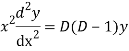
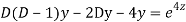
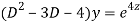
AE is

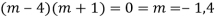
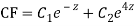
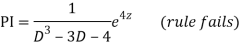
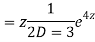
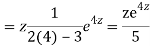
CS = CF + PI

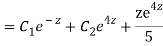
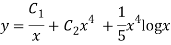
Q12) Solve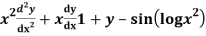

A12)

Let,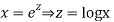

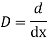
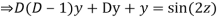
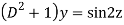
AE is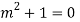

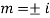
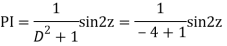
y= CF + PI

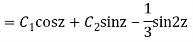
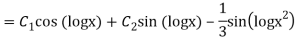
Q13) Solve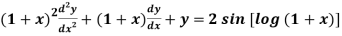

A13)

As we see that this is Legendre’s linear equation.

Now put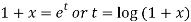

So that-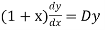

And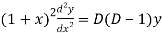

Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t

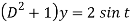
Its auxiliary equation is-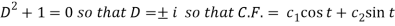

And particular integral-

               P.I. =

Note -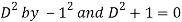

Hence the solution is -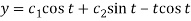

Q14) Solve the following simultaneous differential equations-

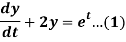
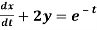....(2)

A14)

Consider the given equations

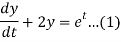
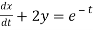....(2)

Consider eq(1),(2)

Dx+2y = et....(1)

Dx +2x =e-t....(2)

Eliminating ‘x’ from both the equations we get,

12 2Dx + 2y = 2et

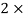D 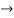2Dx +D2y = e-t

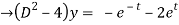
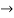y = Ae2t + Be-2t +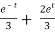

Q15) Solve the following simultaneous differential equations-

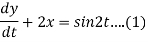
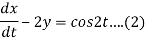
Given that x(0)=1  and y(0)= 0

A15)

Consider the given equations,

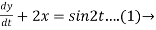Dy +2x = sin2t

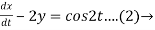Dx -2y = cos2t

By solving the above equations, we get,

(D2 +4)Y =0

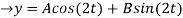
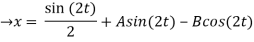
X(0) = 1, y(0) = 0

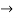A =0, B=-1

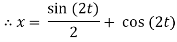
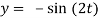
Q16) Solve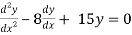                      

 (D2 + 8D + 15)y = 0

A16)

Given,  (D2 + 8D + 15)y = 0

Here Auxiliary equation is

m2 – 8m + 15 = 9

m2 – 3m – 5m + 15 = 0

m(m – 3) – 5(m -3) = 0

(m – 3) (m – 5) = 0

m = 3, 5

y = C1e3x + C2 e5x

Q17) Solve: (D2 + 4)y = Cos 2x

A17)

Auxiliary equation are m2 + 4 = 0

CF = A Cos 2x + B Sin 2x

PI =

Put , D2 = - a2 = -22 = -4

PI =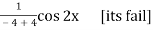

PI = x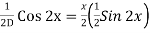

= x/4 Sin 2x

CS = CF + PR

= A Cos 2x + B Sin 2x + x/4 Sin 2x

Q18) Prove that-

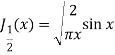
A18)

As we know that-

Jn(x) =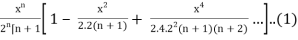

Now put n = 1/2 in equation (1), then we get-

J1/2(x) =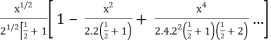

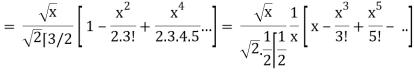
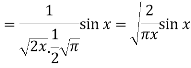
Hence proved.

Q19) Prove that-

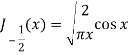
A19)

Put n = -1/2 in equation (1) of the above question, we get-

J1/2(x) =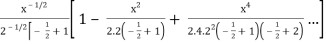

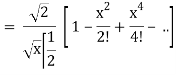
Q20) Show that-

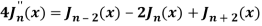
By using recurrence relation.

A20)

We know that-

The recurrence formula-

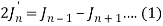
On differentiating, we get-

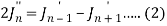
Now replace n by n -1 and n by n+1 in (1), we have-

2 J’n – 1 = Jn – 2 – Jn         or         J’n – 1 = ½  Jn – 2 – ½ Jn

2 J’n+1 = Jn – Jn+2           or         J’n+1 = ½ Jn – ½ Jn+2

Put the values of 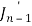and 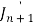from the above equations in (2), we get-

2J’’n = ½ [ Jn-2 – Jn] – ½ [ Jn – Jn + 2]

4J’’n = Jn – 2 – Jn – Jn + Jn+2

4J’’n = Jn – 2 – 2 Jn + Jn+2

Q21) Prove that-

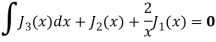
A21)

We know that- from recurrence formula

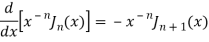
On integrating we get-

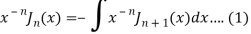
On taking n = 2 in (1), we get-

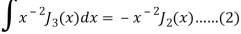
Again-

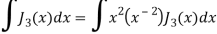
Put the value of 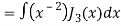from equation (2) and (3), we get-

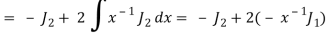
By equation (1), when n = 1

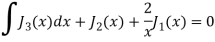
Q22) Express in terms of Legendre polynomials.

A22)

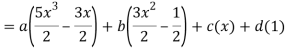
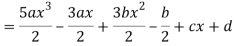
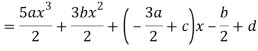
By equating the coefficients of like powers of x, we get-

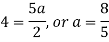
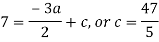
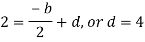
Put these values in equation (1), we get-

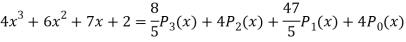
Q23) Let 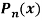be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-

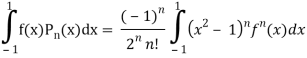
A23)

We know that-

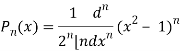
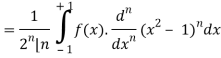
On integrating by parts, we get-

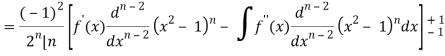
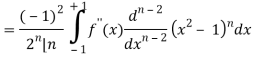
Now integrate (n – 2) times by parts, we get-

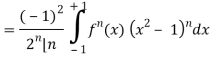
Q24) Show that-

P2n(0) = (-1)n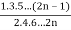

A24)

We know that

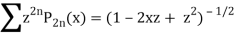
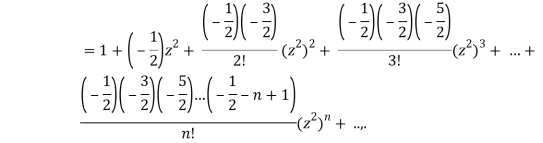
Equating the coefficients of 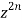both sides, we have-

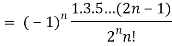
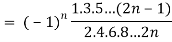
Q25) Prove that-

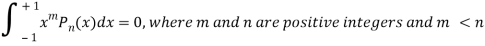
A25)

By using Rodrigue formula for Legendre function.

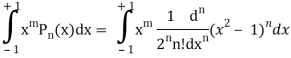
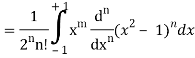
On integrating by parts, we get-

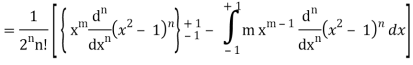
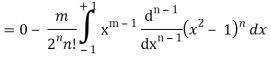
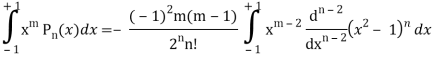
Now integrating m – 2 times, we get-