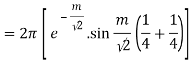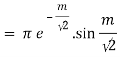Unit - 5
Complex Variable - Integration
Q1) Solve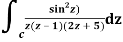 
where 
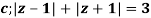
A1)
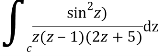
Where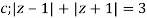 
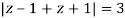
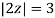
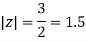
Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1
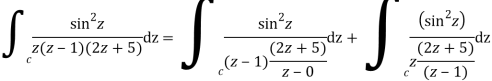
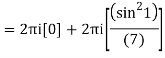
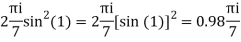
Q2) Solve 
A2)
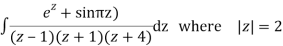
Poles are
|z-0|=2
Poles 1 and -1 inside the circle
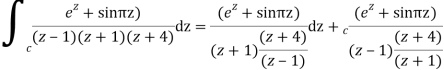
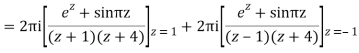
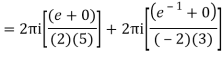
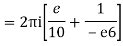
Q3) Solve the following by cauchy’s integral method:
f(n)(a) = n!/2πi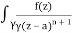 
A3)
Given,
f(n)(a) = n!/2πi 
f(k + 1)(a) = d/da f(k)(a)
= k!/2πi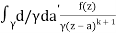 
= k!/2πi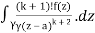 
= (k+1)!/2πi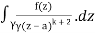 
Q4) Evaluate 
dz by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
A4)
It is given that-
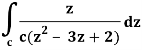
Find its poles by equating denominator equals to zero.
z2 – 3z + 2 = 0
(z – 1)(z – 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-
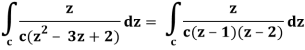
Now by using Cauchy’s integral formula, we get-
= 2πi [ z / z-1]z = 2 = 2πi(2/2 -1) = 4πi
Q5) Evaluate the integral given below by using Cauchy’s integral formula-
A5)
Here we have-
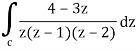
Find its poles by equating denominator equals to zero.
z(z – 1)(z – 2) = 0
We get-
z = 0,1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
= 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2πi . 4/(-1)(-2) + 2πi (4 -3)/1(1 -2) = 2πi(2 – 1) = 2πi
Q6) Evaluate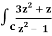 
dz if c is circle |z - 1| = 1.
A6)
Here we have-
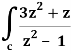
Find its poles by equating denominator equals to zero.
z2 – 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
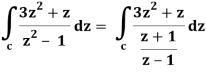= 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 4πi
Q7) Find out the zero of the following-
f(z) = (z – 2)/z2 sin 1/(z – 1)
A7)
Zeroes of the function-
f(z) = 0
(z – 2)/z2 sin 1/(z – 1) = 0
(z – 2)/z2 = 0, sin 1/(z – 1) = 0
z = 2, 1/(z – 1) = nπ ( n = 0, ±1, ±2 ….)
z = 2, 1 + 1/nπ (n = 0, ±1, ±2 ….)
Q8) Find the singularity of the function-
f(z) = sin 1/z
A8)
As we know that-f(z) = a0 +a1(z – a) + a2(z – a)2 + . . . + 1/(z – a)m[ b1(z – a)m – 1 + b2(z – a)m – 2 + b3(z – a)m – 3 + . . . + bm}
So that there is a number of singularity.
Sin 1/z is not analytic at z = a
(1/z = ∞ at z = 0)
Q9) Find the singularity of 1/(1 – ez) at z = 2πi
A9)
Here we have-
f(z) = 1/(1 – ez)
We find the poles by putting the denominator equals to zero.
That means-
1 – ez = 0
ez = 0 = ( cos 2n π + i sin 2n π) = e2nπi
z = 2nπi(n = 0, ±1, ±2, ….)
z = 2n π i is a simple pole
Q10) Determine the poles of the function-
f(z) = 1/(z4 +1)
A10)
Here we have-
f(z) = 1/(z4+1)
We find the poles by putting the denominator of the function equals to zero-
We get-
z4 + 1 = 0 and z4 = - 1
f(z) = a0 + a1(z – a) + a2(z – a)2 + . . . + b1/z - a
By De Moivre’s theorem-
Sin 1/z = 1/z – 1/3!z3 + 1/5!z5 + . ….+ (-1)n 1/(2n+1)! z2n+1
z = (-1)1/4 = (cos π + i sin π)1/4
If n = 0, then pole-
= [ cos (2n + 1)π + i sin (2n + 1)π]1/4
If n = 1, then pole-
= [ cos (2n + 1)π/4 + i sin (2n+1)π/4]
If n = 2, then pole-
z = [ cos π/4 + i sin π/4] = (1/2 + i 1/2)
If n = 3, then pole-
z = [ cos 3π/4 + i sin 3π/4] = (- 1/2 + i 1/2)
Q11) Expand the function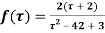
In a Taylor's series about the point
A11)
Using partial fraction method
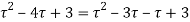
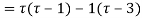
(τ-1)(τ-3)
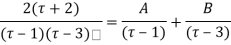
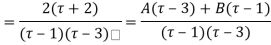
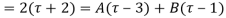
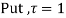
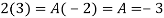
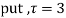
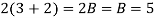
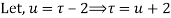
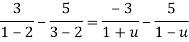
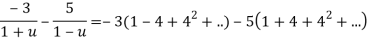
Both series converge when |4|<1
Therefore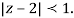 
The series converges in the circle centred at
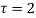with radius of 1.
Taylor’s series expansion is
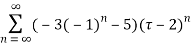
Q12) Show that when 0<|z|<4
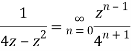
A12)
When |z|<4 we have
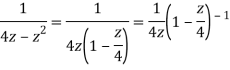
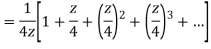
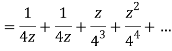
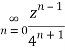
Q13) Expand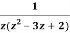 
for the regions
- 0<|z|<1
- 1<|z|<2
- |z|>2
A13)
Let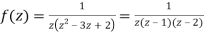 
Hence resolving into partial functions we get
1) For 0<|z|<1 we have
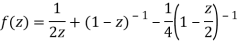
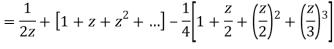
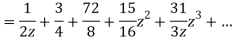
2) For 1<|z|<2 we have
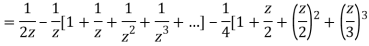
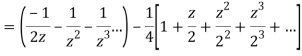
3) For |z|>2 we have
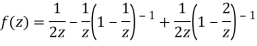
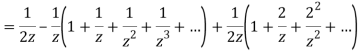
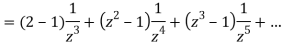
Q14) Obtain the Taylor’s and Laurent’s series which represents the function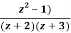 
in the regions
1) |z|<2
2) 2<|z|<3
3) |z|>3
A14)
We have
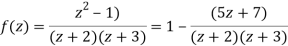
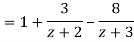
1) For |z|<2 we have
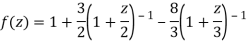
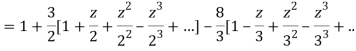
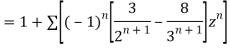
Which is Taylor’s series valid for |z|<2
2) For 2<|z|<3 we have
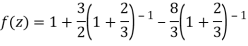
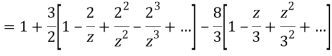
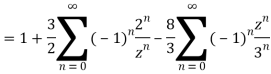
3) For |z|<3
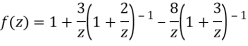
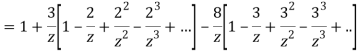
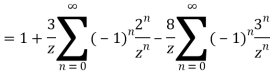
Q15) Find residue of the function
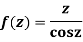
A15)
Let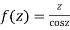 
The singularities of f(z) are given by 
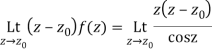
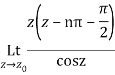
Which is of the form 
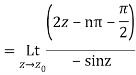
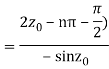
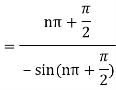
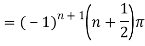
Q16) Find the residue of 
at z=1
A16)
Let f(z)=
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=
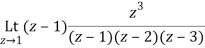
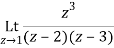
=1/2
Q17) Find the residue of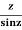 
A17)
f(z)=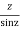
Poles are determined by putting sinz=0=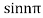
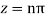
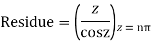
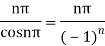
Hence the residue of the given function at pole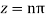 
is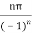 
Q18) Evaluate the following integral using residue theorem
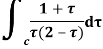
Where c is the circle.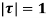
.
A18)
The poles of the integral are given by putting the denominator equal to zero
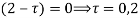
The integral is analytic on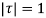 
and all points inside except
as a pole at 
is inside the circle
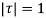
Hence by residue theorem
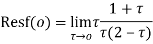
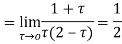
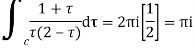
Q19) Evaluate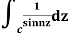 
where c;|z|=4
A19)
Here f(z)=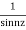
Poles are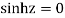 
Sin iz=0
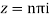
Poles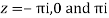 
Lie inside the circle |z|=4
The given function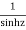 
is of the form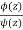 
Its pole at z=a is 
Residue (at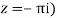 
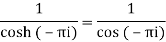
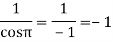
Residue at z=0=
Residue at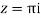 
=
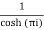
Residue at 
are
Respectively -1,1 and -1
Hence the required integrand
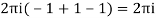
Q20) Prove that 
A20)
Let 
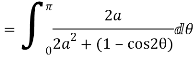
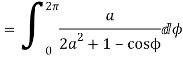
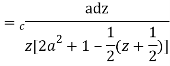
Putting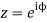 
where c is the unit circle |z|=1
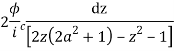
2ai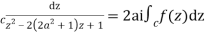
Poles of f(z) are given by the roots of
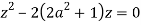
Or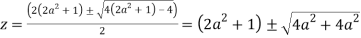 
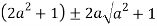
Let 
Clearly 
and since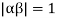 
we have 
Hence the only pole inside c is at z=
Residue (at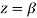 
)
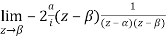
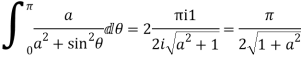
Q21) Evaluate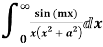 
A21)
Consider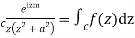 
Where c is the closed contour consisting of
1) Real axis from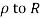 
2) Large semicircle in the upper half plane given by |z|=R
3) The real axis -R to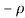 
and
4) Small semicircle given by |z|=
Now f(z) has simple poles at z=0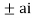 
of which only z=
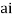is avoided by indentation
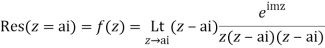
Hence by Cauchy’s Residue theorem
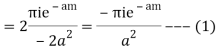
Since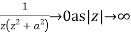 
and
Hence by Jordan’s Lemma 
Also since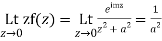 
Hence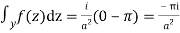 
Hence as 
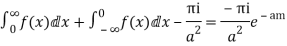
Equating imaginary parts we get
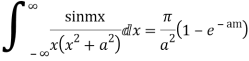
Q22) Prove that 
A22)
Consider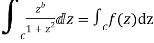 
Where c is the contour consisting of a large semicircle in the upper half plane indented at the origin as shown in the figure
Here we have avoided the branch point o, of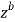 
by indenting the origin
Then only simple of f(z) within c is at z=i
The residue(at z=i) =
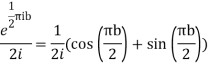
Hence by residue theorem
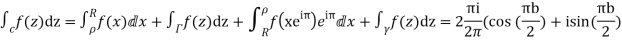
Since 
on -ve real axis.
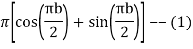
Now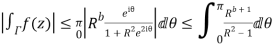 
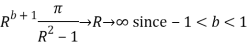
Similarly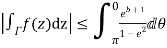
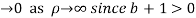
Hence when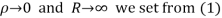 
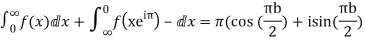
Equating real parts we get
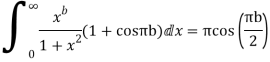
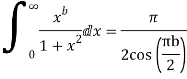
Q23) Evaluate-
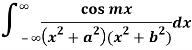
A23)
We know that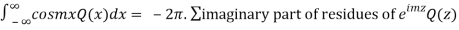 
atits poles in the upper half plane. So consider
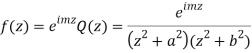
(z) has simple poles at z = ±ai, z = ±bi out of which z = ai, bi lies in the upper half plane.
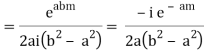
Similarly,
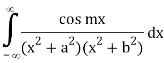
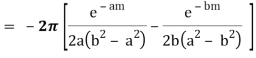
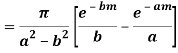
Q24) Evaluate:
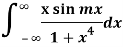
A24)
We know that 
atits poles in the upper half plane.
So consider 
which has singular points at z =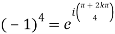 
for k = 0, 1, 2, 3. Out of these four, only 
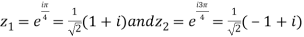lies in the
Upper half plane.
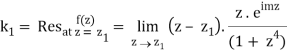
Which is 0/0 form, Applying L’ Hostpital’s rule
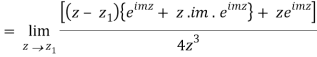
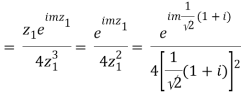
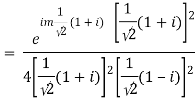
Real part of k1 = ¼ e-m/2 . Sin m/2
Similarly
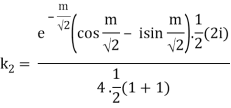
Real part of k2 = ¼ e- m/2 . Sin m/2
Then
