Unit - 1
Coordinate Systems and Transformation
Q1) Obtain the unit vector in the direction from the origin towards the point P(3,-3,-2)
A1)
The origin O(0,0,0) while P(3,-3,-2) hence the distance vector 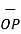 is
is
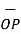 = (3-0)
= (3-0) 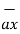 + (-3-0)
+ (-3-0) 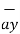 +(-2-0)
+(-2-0) 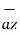 = 3
= 3 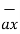 -3
-3  -2
-2 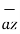
 =
= 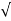 (3) 2 + (-3) 2 + (-2) 2 = 4.6904
(3) 2 + (-3) 2 + (-2) 2 = 4.6904
Hence the unit vector along the direction OP is
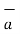 OP=
OP= 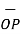 / |
/ |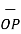 | = 3
| = 3 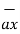 -3
-3  -2
-2 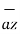 / 4.6904 =
/ 4.6904 =
= 0.6396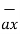 -0.63963
-0.63963 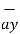 -0.4264
-0.4264 
Q2) Given the three points in cartesian co-ordinate system as A(3,-2,1) B (-3,-3,5) , C (2,6,-4)
Find
i) The vector from A to C
Ii) The unit vector from B to A
Iii) The distance from B to C
Iv) The vector from A to the mid-point of the straight line joining B to C.
A2)
The position vectors for the given points are:
 = 3
= 3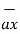 - 2
- 2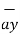 +
+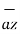 .
.
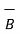 = -3
= -3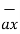 - 3
- 3 +5
+5  .
.
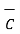 = 2
= 2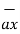 +6
+6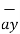 -4
-4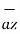 .
.
i) The vector from A to C is
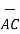 =
= 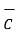 -
- 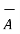 = [ 2-3]
= [ 2-3] 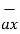 +[6–(-2)]
+[6–(-2)]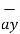 +[-4-1]
+[-4-1] 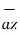 .
.
= - 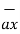 + 8
+ 8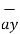 -5
-5 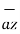 .
.
Ii) For unit vector from B to A obtain the distance vector 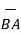 first
first
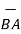 =
=  -
- 
= [ 3 – (-3)]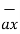 + [ (-2) –(-3) ]
+ [ (-2) –(-3) ] 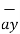 + [ -4-1]
+ [ -4-1] 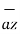
= 6 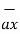 +
+ 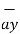 -4
-4 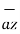 .
.
|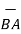 | =
| = 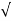 (6) 2 + (1) 2 + (-4)2 = 7.2801.
(6) 2 + (1) 2 + (-4)2 = 7.2801.
 BA =
BA = 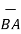 / |
/ |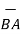 | = 6
| = 6  +
+ 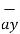 -4
-4  ./ 7.2801
./ 7.2801
Iii) For distance between B and C
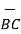 =
= 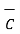 -
- 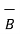 = [ 2 –(-3 ]
= [ 2 –(-3 ] 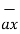 + [6-(-3)]
+ [6-(-3)] 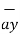 +[-4) –(-5)]
+[-4) –(-5)] 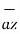 = 5
= 5 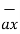 + 9
+ 9 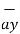 – 9
– 9 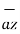
Distance BC =  2 + (9) 2 + (-9) 2 = 13.6747
2 + (9) 2 + (-9) 2 = 13.6747
Iv) Let B(x1,y1,z1 ) and C(x2,y2,z2) then the co-ordinates of the mid-point BC are (x1+x2/2 , y1+y2/2 , z1+z2/2)
Q3) Evaluate 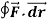 where F= cos y.i-x siny j and C is the curve y=
where F= cos y.i-x siny j and C is the curve y=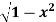 in the xy plae from (1,0) to (0,1)
in the xy plae from (1,0) to (0,1)
A3)
The curve y i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
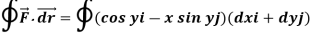


Q4) Evaluate 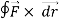 where
where 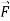 = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
A4)
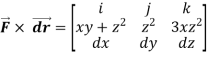
Put 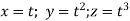
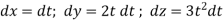

=(3t4-6t8) dti – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
=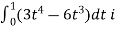 –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
–(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
=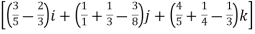
=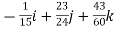
Q5) Prove that ͞͞͞F = [y2cos x +z3] i+(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for͞͞͞ F (ii) the work done in moving an object in this field from (0, 1, -1) to (π/ 2,-1, 2)
A5)
(a) The fleld is conservative if cur͞͞͞͞͞͞F = 0.
Now, curl͞͞͞F = 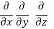
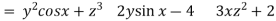
Curl F= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
∴(y2cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =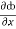 i +
i +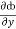 j +
j +  k
k
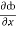 = y2cos x + z3,
= y2cos x + z3,  = 2y sin x – 4,
= 2y sin x – 4,  = 3xz2 + 2
= 3xz2 + 2
Now, 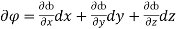
= (y2cos x + z3) dx +(2y sin x – 4)dy + (3xz2 + 2)dz
= (y2cos x dx + 2y sin x dy) +(z3dx +3xz2dz) +(- 4 dy) + (2 dz)
=d(y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =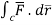
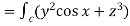 dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
=  (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z ]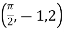
= [ 1 +8π/2 + 4 + 4 ] – { - 4 – 2} =4π + 15
Q6) Evaluate 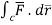 where
where  =yz i+zx j+xy k and C is the position of the curve.
=yz i+zx j+xy k and C is the position of the curve.
 = (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
= (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
A6)
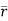 = (a cost)i+(b sint)j+ct k
= (a cost)i+(b sint)j+ct k
The parametric eqn. Of the curve are x= a cost, y=b sint, z=ct (i)

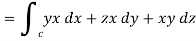
Putting values of x,y,z from (i),
Dx=-a sint
Dy=b cost
Dz=c dt
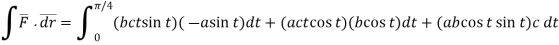
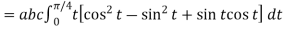
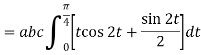
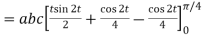
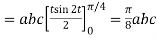
Q7) Find the circulation of 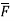 around the curve C where
around the curve C where 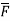 =yi+zj+xk and C is circle
=yi+zj+xk and C is circle 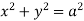 .
.
A7)
Parametric eqn of circle are:
x=a cos θ
y=a sin θ
z=0
 =xi+yj+zk = a cos θ i + b cos θj + 0 k
=xi+yj+zk = a cos θ i + b cos θj + 0 k
d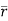 =(-a sinθ i + a cos θj)d θ
=(-a sinθ i + a cos θj)d θ
Circulation =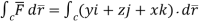
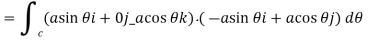
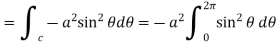


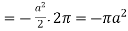
Q8) Evaluate 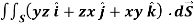 , where S is the surface of the sphere
, where S is the surface of the sphere 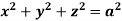 in the first octant.
in the first octant.
A8)
Here-
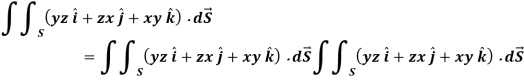
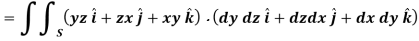
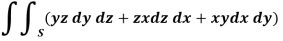
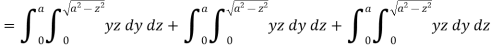
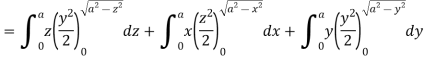
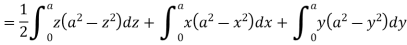
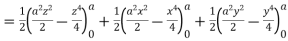
Which becomes-
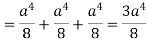
Q9) Evaluate 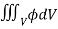 , where
, where 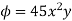 and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
A9)
Here- 4x + 2y + z = 8
Put y = 0 and z = 0 in this, we get
4x = 8 or x = 2
Limit of x varies from 0 to 2 and y varies from 0 to 4 – 2x
And z varies from 0 to 8 – 4x – 2y
So that-
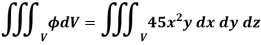
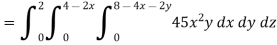

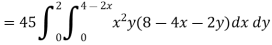
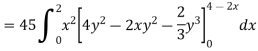
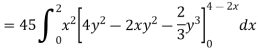
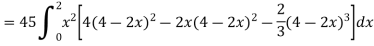
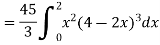

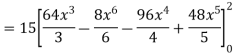
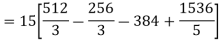
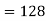
So that-

Q10) Evaluate 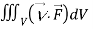 if V is the region in the first octant bounded by
if V is the region in the first octant bounded by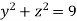 and the plane x = 2 and
and the plane x = 2 and .
.
A10)
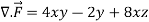
x varies from 0 to 2
The volume will be-

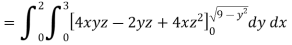
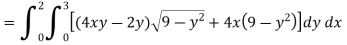
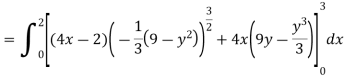
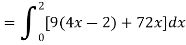
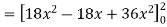

Q11) Find its gradient at P(0,1,1) for cartesian, 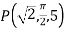 for cylindrical and
for cylindrical and 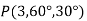 for the spherical.
for the spherical.
A11)
a) 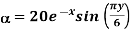 in Cartesian
in Cartesian
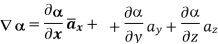
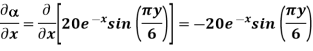

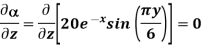

 At P (0,1,1) the
At P (0,1,1) the 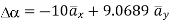

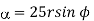 in cylindrical.
in cylindrical.
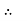 =
=

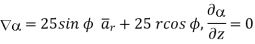
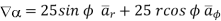
At 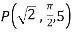 the =
the =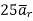
Q12) A scalar field is given by
a) 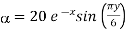 … In Cartesian
… In Cartesian
b) 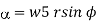 … In cylindrical
… In cylindrical
c) 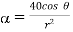 … In spherical
… In spherical
Find its gradient at P(0,1,1) for cartesian, 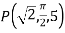 for cylindrical and
for cylindrical and  for the spherical.
for the spherical.
A12)
a) 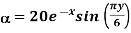 in Cartesian
in Cartesian

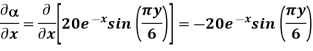
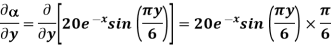


 At P (0,1,1) the
At P (0,1,1) the 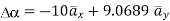
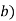
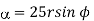 in cylindrical.
in cylindrical.
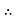 =
=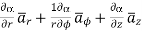
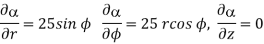
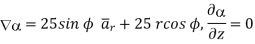
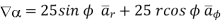
At 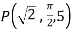 the =
the =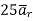
c) 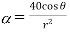 in spherical
in spherical
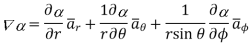
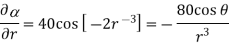

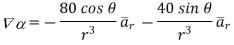

Q13) Define Coulombs Law?
A13) It states that force between two point charges Q1 and Q2
- Acts along the line joining the two point charges.
- Is directly proportional to the product of Q1Q2 of the two charges
- Is inversely proportional to the square of the distance between them.
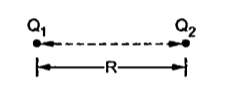
Figure. Two point charge
Consider two point charges Q1 and Q2 as shown in the figure seperated by distance R. The charge Q1 exerts a force on Q2 while Q2 also exerts a force on Q1. The force acts along the line joining Q1 and Q2. The force exerted between them is repulsive if the chrages are of same polarity while it is attractive if the charges are of different polarity.
Mathematically the force F between the charges can be expressed as ,
F α Q1Q2/ R 2
Q1Q2------ Product of two charges
R ------- Distance between the two charges
The law also states that the force depends on the medium in which the point charges are located. The effect of medium is introduced in the equation of force as a constant of proportionality denoted as k.
F = k . Q1 Q2/ R2
The constant of proportionality takes into account the effect of medium.
Therefore,
k = 1/ 4 π 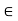
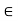 = Permittivity of medium in which charges are located . The units of
= Permittivity of medium in which charges are located . The units of 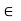 are farads/metre(F/m)
are farads/metre(F/m)
In general  is expressed as,
is expressed as,
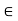 =
= 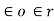
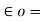 Permittivity of free space or vacuum
Permittivity of free space or vacuum
 = Relative permittivity or dielectric constant of the medium with respect to free space.
= Relative permittivity or dielectric constant of the medium with respect to free space.
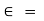 Absolute permittivity
Absolute permittivity
For free space or vacuum the relative permittivity 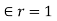 hence
hence
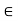 =
= 
F = 1/ 4 π  . Q1Q2/ R2
. Q1Q2/ R2
The value of permittivity of free space 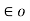 is
is
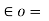 1/ 36 π x 10 -9 = 8.854 x 10 -12 F/m
1/ 36 π x 10 -9 = 8.854 x 10 -12 F/m
k = 1/ 4π  = 1/ 4π x 8.854 x 10 -12 = 8.98 x 10 9 = 9 x 10 9 m/F
= 1/ 4π x 8.854 x 10 -12 = 8.98 x 10 9 = 9 x 10 9 m/F
Hence the Coulombs law can be expressed as ,
F = Q1 Q2 / 4π 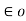 R 2
R 2
This the force between the two point charges located in free space or vacuum.
Q14) Define electric field intensity and also derive its expression?
A14) Consider a point charge Q1 as shown in figure:
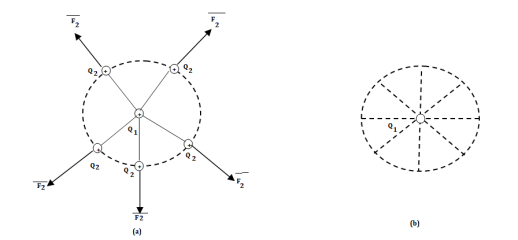
Fig: Electric Field Intensity
If any other similar charge Q2 is brought near it Q2 experiences a force. Infact if Q2 is moved around Q1 still Q2 experiences a force as shown in figure.
Thus there exists a region around a charge in which it exerts force on any other charge. This region where a particular charge exerts a force on any other chrge located in that region called electric field of that charge . The electric field of Q1 is shown in figure (b).
The force experienced by the charge Q2 due to Q1 is given by Coulombs law as ,

Thus, force per unit charge can be written as:

This force exerted per unit charge is called electric field intensity or electric field strength. It is a vector quantity and is directed along a segment from the charge Q1 to the position of any other charge.
It is denoted as 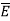 .
.
Another definition of electric field is the force experienced by a unit positive test charge that is Q2 = 1C.
Consider a charge Q1 as shown in figure below. The unit positive charge Q2=1C is placed at distance R from Q1. Then the force acting on Q2 due to Q1 is along the unit vector 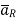 As the charge Q2 is unit charge the force exerted on Q2 is nothing but electric field intensity
As the charge Q2 is unit charge the force exerted on Q2 is nothing but electric field intensity 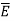 of Q1. Then the force acting on Q2 due to Q1 is along the unit vector
of Q1. Then the force acting on Q2 due to Q1 is along the unit vector 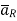 . As the charge Q2 is unit charge the force exerted onQ2 is nothing but electric field intensity
. As the charge Q2 is unit charge the force exerted onQ2 is nothing but electric field intensity 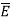 of Q1 at a point where unit charge is placed.
of Q1 at a point where unit charge is placed.
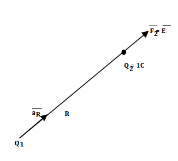
Fig: Concept of electric field intensity

If a charge Q1 is located at the centre of the spherical coordinate system then unit vector 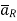 in equation (3) becomes the radial unit vector
in equation (3) becomes the radial unit vector 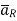 coming radially outwards from Q1 and the distance R is the radius of the sphere r.
coming radially outwards from Q1 and the distance R is the radius of the sphere r.
Q15) Define Gauss Law and also prove it?
A15) The surface integral of electrostatic field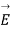 produced by any source over any closed surface S enclosing a volume V in vacuum i.e. total electric flux over the closed surface S in vacuum is X the total charge (
produced by any source over any closed surface S enclosing a volume V in vacuum i.e. total electric flux over the closed surface S in vacuum is X the total charge ( ) contained inside S i.e.
) contained inside S i.e.
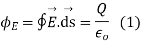
The charge inside S maybe point charges as well as continuous charge distributions.
The surface chosen to calculate the surface integral is called Gaussian surface.
Proof:
Suppose an isolated positive point charge q is situated at the centre of the sphere of radius r,
According to coulomb’s law, electric field intensity at every point on the surface of the sphere is
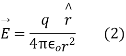
Where is unit vector directed from +q to the surface element
is unit vector directed from +q to the surface element
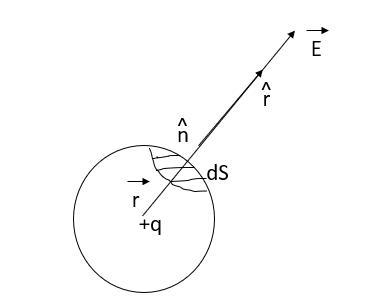
Fig: Charge q at centre of Sphere
Consider small area element ds represented by the vector where is unit vector  along out drawn normal to the area element
along out drawn normal to the area element
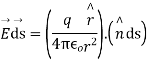
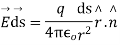

Integrating over the closed surface area of sphere we get
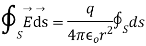
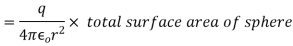
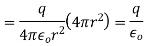
Which proves gauss theorem.
If there are two point charges 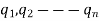 lying inside the surface, each will contribute the electric flux independent of the others.
lying inside the surface, each will contribute the electric flux independent of the others.
(Superposition principle)
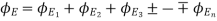
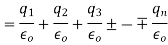

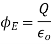
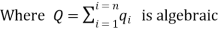 sum of all the charges inside the closed surface if the medium surrounding the charge has a dielectric constant K then
sum of all the charges inside the closed surface if the medium surrounding the charge has a dielectric constant K then
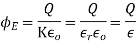
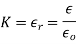
If there is no net charge within the closed surface that is
Q16) Derive Poisons equation?
A16) From the Gauss’s law in the point form Poisson’s equation can be derived. Consider the Gauss’s law in the point form as
 .
.  =
= 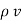
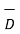 = flux density
= flux density
 Volume charge density.
Volume charge density.
For a homogeneous isotropic and linear medium, flux density and the electric field are directly proportional. Thus,
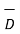 =
= 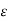 .
. 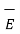
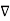 .
. 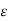 .
. 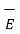 =
= 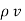
From the gradient relationship
E = -  . V
. V
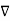 .
. 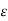 (-
(-  . V) =
. V) = 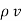
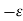 (
( 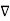 .
. 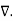 V) =
V) = 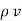
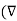 .
. 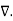 V) =-
V) =- 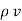 /
/ 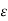
Now  .
.  operation is called ‘del squared’ operation denoted as
operation is called ‘del squared’ operation denoted as  2.
2.
 2. V = -
2. V = - 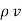 /
/ 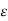
This equation is called as Poisson’s Equation
Q17) Derive Laplace equation and mention the application of Laplace and Poisons equation?
A17) If in a certain region volume charge density is zero ( 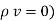 which is true for dielectric medium then the Poisson’s equation takes the form,
which is true for dielectric medium then the Poisson’s equation takes the form,
 2. V =0.
2. V =0.
This equation is called Laplace’s equation.
Application of Laplace and Poisson’s Equations
Using Laplace or Poisson’s equation we obtain:
- Potential at any point in between two surfaces when potential at two surfaces is given.
- We can also obtain capacitance between these two surfaces.
Q18) Define curl of a vector derive expression?
A18) The circulation of a vector field around closed path is given by curl of vector. Mathematically it is defined as
Curl of 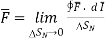
Where 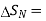 Area enclosed by the line integral in normal direction
Area enclosed by the line integral in normal direction
Thus, maximum circulation of 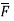 per unit area tends to zero whose direction is normal to the surface is called curl of
per unit area tends to zero whose direction is normal to the surface is called curl of 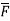 .
.
Symbolically it is represented as 
In various co-ordinate system, the curl of 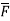 is given by,
is given by,

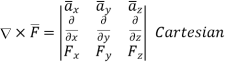 (3)
(3)
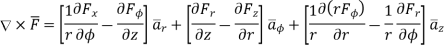
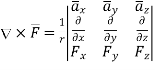 Cylindrical
Cylindrical
In 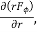 r cannot be taken outside as differential is with respect to
r cannot be taken outside as differential is with respect to
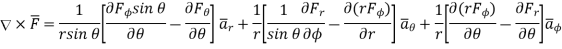
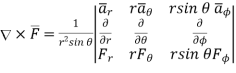 Spherical
Spherical
Q19) Define divergence and explain what id divergence of a vector?
A19)  gives the flux flowing across surface S. Then mathematically divergence is defined as the net outward flow of the flux per unit volume over a closed incremental surface. It is denoted as div
gives the flux flowing across surface S. Then mathematically divergence is defined as the net outward flow of the flux per unit volume over a closed incremental surface. It is denoted as div  given by
given by
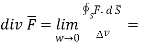 Divergence of
Divergence of 
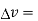 Differential volume element
Differential volume element
Symbolically it is denoted as,
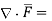 Divergence of
Divergence of 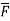
Where =Vector operator =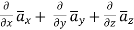
But 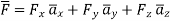
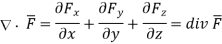
This is divergence of 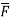 in Cartesian system.
in Cartesian system.
Similarly, divergence in other co-ordinate systems are,
 cylindrical
cylindrical
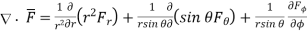 spherical
spherical
Physically divergence at a point indicate how much that vector field diverges from that point.
Consider a sloenoid that is the elctromagnet obtained by winding a coil around the core. When current passes through it flux produced around it. Such a flux completes a closed path through the solenoid hence solenoid field does not diverge. Therefore the vector field having its divergence zero is called solenoidal field.
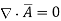 for
for 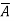 to be solenoidal
to be solenoidal