Unit – 2

Numerical Method

Q1) What is finite difference?

A1)

Finite Difference:

Let be a function of x. The table given below gives corresponding values of y for different values of x.

X				….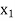
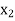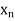y= f(x)				….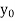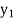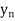

Forward Difference: 

Then  are called differences of y, denoted by 

The symbol is called the forward difference operator.  Consider the forward difference table below:

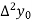
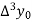
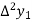
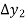
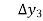
Where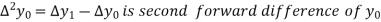

And 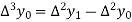third forward difference so on.

Backward Difference:

The difference 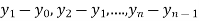are called first backward difference and  is denoted by  Consider the backward  difference  table  below:

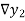
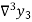
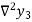
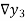
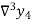
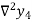
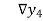
Where

And third backward differences so on.

Q2) Prove that

A2)

We know that,

Or

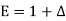
Q3) Show that

A3)

Q4) Using Newton’s forward difference formula, find the sum

A4)

Putting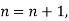

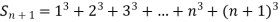
It   follows that

Since is a fourth-degree polynomial in n.

Further,

By Newton Forward Difference Method

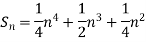
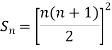
Q5) Find the missing term in the following)

	0	1	2	3	4
	1	3	9	?	81

A5)

Let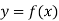

First, we construct the forward difference table:

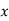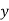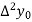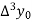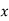
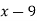
0       1        2        3        4	1       3       9         81	2         6	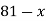4

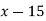
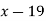
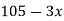Now,

Q6) What is Newton backward difference method?

A6)

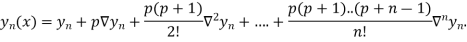
Where 

Q7) The following table give the amount of a chemical dissolved in water)

Temp.
Solubility	19.97	21.51	22.47	23.52	24.65	25.89

Compute the amount dissolve at

A7)

Consider the following backward difference table:

Temp.  x	Solubility y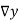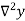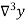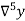
10     15     20     25     30     35	19.97      21.51     22.47     23.52      24.65      25.89	1.54     0.96    1.05     1.13     1.24	-0.58      0.09      0.08      0.11	0.67     -0.01      0.03	-0.68     0.04	0.72

Here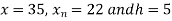

By Newton Backward difference formula

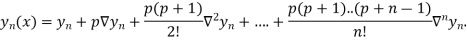
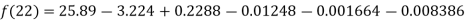
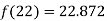
Q8) What is Lagrange’s interpolation of polynomial.

A8)

Let , be defined function we get

X				…..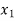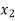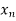
f(x)				……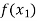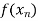

Where the interval is not necessarily equal. We assume f(x) is a polynomial od degree n.  Then Lagrange’s interpolation formula is given by

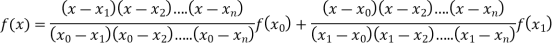
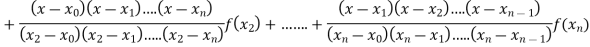
Q9) By means of Lagrange’s formula, prove that

A9)

We construct the table:

X	0	1	2	3	4	5	6
Y=f(x)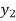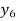

Here x = 3, f(x)=?

By Lagrange’s formula for   interpolation

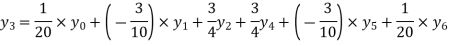
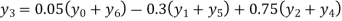
Hence proved.

Q10) What is inverse interpolation?

A10)

Inverse Interpolation (Lagrange’s Method)

Given a set of values of x and y, the process of finding the value of x  for a certain value of y is called inverse interpolation.

Lagrange’s Inverse interpolation:

Let 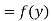, be  defined  function we get

x				…..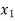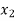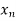
f(Y)				……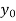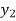

Where the interval is not necessarily equal. We assume f(x) is a polynomial of degree n.  Then Lagrange’s inverse interpolation formula is given by

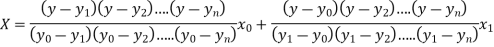
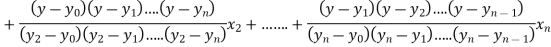
Q11) Use the inverse   Lagrange’s method to find the root of the equation , give data

A11)

Here , we have the  data

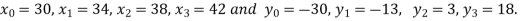
Also.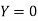

The Lagrange’s inverse interpolation formula is given by

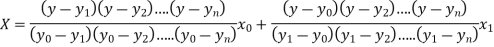
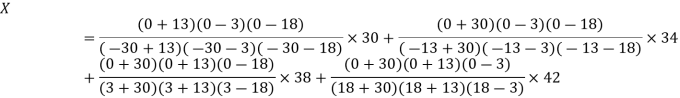
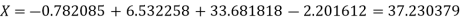
Thus the approximate   root of the given equation is .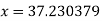

Q12) Given that

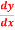Find at .

A12)

Here the first derivative is to be calculated at the beginning of the table, therefore forward difference  formula will be used

Forward difference table is given below:

X	Y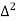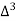
1.0   1.1   1.2   1.3	0.841   0.891   0.932   0.962	0.050   0.041   0.031	-0.009   -0.010	-0.001

By Newton’s forward differentiation formula for differentiation

Here 

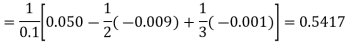
Q13) Given that

Find ?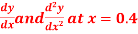

A13)

Backward difference table:

X	Y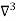
0.1   0.2   0.3   0.4	1.10517   1.22140   1.34986   1.49182	0.11623   0.12846   0.14196	0.01223   0.01350	0.00127

Newton’s Backward formula for differentiation

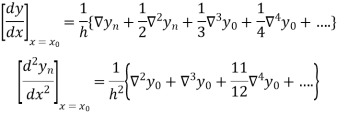
Here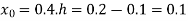

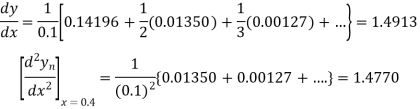
Q14) What is Newton cotes quadrature formula?

A14)

Suppose 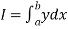where y takes the values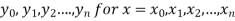

And let the integration interval (a,b) is divided into n equal sub-intervals, each of width h = b – a /n, so that,

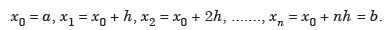
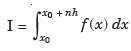
...(1)

The above formula is known as Newton’s cotes formula.

This is also known as general quadrature formula.

Q15) Compute the value of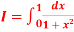  

A15)

Using the trapezoidal rule with h=0.5, 0.25 and 0.125.

Here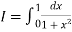

For h=0.5, we construct the data table:

By Trapezoidal rule

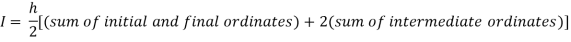
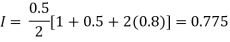
For h=0.25, we construct the data table:

By Trapezoidal rule

For h = 0.125, we construct the data table:

By Trapezoidal rule

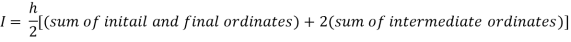
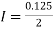[(1+0.5) +2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]

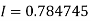
Q16) Evaluate the following integral by using Simpson’s 1/3rd and 3/8th rule.

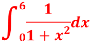
A16)

First, we will divide the interval into six parts, where width (h) = 1, the value of f(x) is given in the table below-

x	0	1	2	3	4	5	6
f(x)	1	0.5	0.2	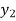0.1	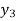1/17 = 0.05884	1/26 = 0.0385	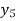1/37 = 0.027

Now using Simpson’s 1/3rd rule-

We get-

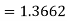
And now

Now using Simpson’s 3/8th rule-

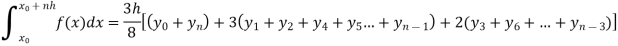
Q17) Estimate the value of the integral

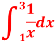
A17)

By Simpson’s rule with 4 strips and 8 strips respectively.

For n=4, we have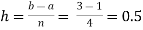

E construct the data table:

By Simpson’s Rule

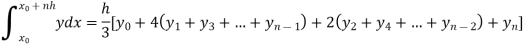
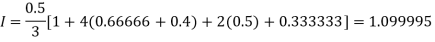
For n = 8, we have

By Simpson’s Rule

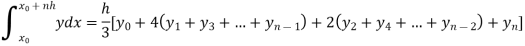
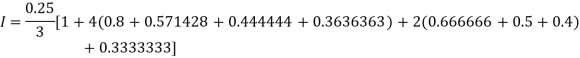
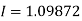
Q18) Using Simpson’s 1/3 rule with h = 1, evaluate

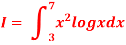
A18)

For h = 1, we construct the data table:

X	3	4	5	6	7
	9.88751	22.108709	40.23594	64.503340	95.34959

By Simpson’s Rule

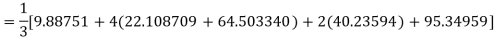
= 177.3853

Q19) Evaluate

A19)

Let us divide the range of the interval [0,6] into six equal parts.

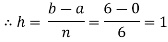
For h=1, we construct the data table:

X	0	1	2	3	4	5	6
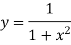	1	0.5	0.2	0.1	0.0588	0.0385	0.027

By Simpson’s 3/8 rule

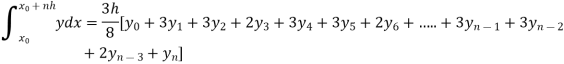
+3(0.0385) +0.027]

=1.3571