Unit - 2
Resonance
Q1) Calculate the phasor currents I1 and I2 in the circuit of Figure below
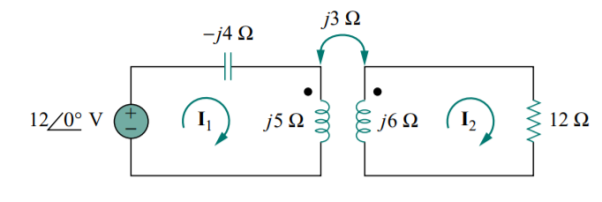
A1) For coil 1, KVL gives
−12 + (−j4 + j5) I1 − j3I2 = 0
j I1 − j3I2 = 12
For coil 2, KVL gives
−j3I1 + (12 + j6) I2 = 0
I1 =  = (2-4j) I2
= (2-4j) I2
(j2 + 4 − j3) I2 = (4 − j) I2 = 12
I2 =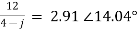 A
A
I1 = (2 − j4) I2 = 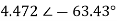 )
)  ) =
) = 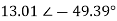 A
A
Q2) Calculate the mesh currents in the circuit of Figure below

A2) The mutual voltage is V1 = −2j I2.
For mesh 1 applying KVL we have
−100 + I1(4 − j3 + j6) − j6I2 − j2I2 = 0
100 = (4 + j3) I1 − j8I2
Applying the dot convention gives the mutual voltage as V2 = −2j I1. Also, current I2 sees the two coupled coils in series; since it leaves the dotted terminals in both coils. Therefore, for mesh 2, KVL gives
0 = −2j I1 − j6I1 + (j6 + j8 + j2 × 2 + 5) I2
0 = −j8I1 + (5 + j18) I2
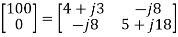
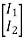
The determinants are
 =
= 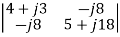 = 30+j87
= 30+j87
 =
= 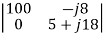 = 100(5+j18)
= 100(5+j18)
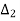 =
= 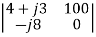 = j800
= j800
Thus, we obtain the mesh currents as
I1 = 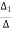 =
= 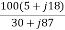 =
=  = 20.3
= 20.3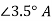
I2 =  =
= 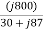 =
= 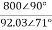 = 8.693
= 8.693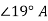
Q3) Estimate the currents for the circuit in figure using the Kirchhoff’s laws
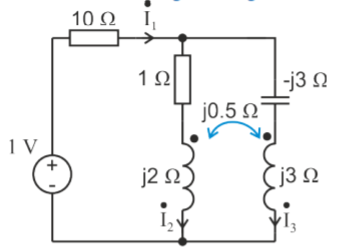
A3) It can be seen that the mutual inductance jωM is given as mutual resistance jω M= j0.5 Ω
Firstly, we are going to create an equivalent circuit by replacing the mutual inductance with dependent source. Since both currents 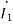 and
and 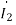 enter the dots, the dependent sources are with plus sign. Next, we write the system of equations:
enter the dots, the dependent sources are with plus sign. Next, we write the system of equations:
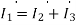
1-0.5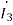 =10
=10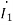 +(1+j2)
+(1+j2) 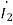
0.5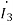 -0.5
-0.5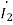 = -(1+j2)
= -(1+j2)  +0
+0 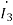
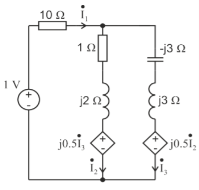
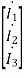
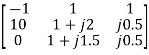 =
= 
The determinants are
 =
= 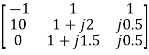 =10.25+j10
=10.25+j10
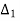 =
= 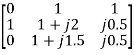 = 1+j
= 1+j
 =
=  = -j0.5
= -j0.5
 =
= 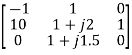 = 1+j1.5
= 1+j1.5
The value of currents will be
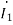 =
= 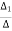 =
= 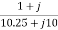 =
= 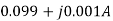
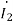 =
=  =
= 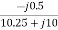 =
= 
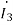 =
= 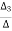 =
= 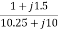 =
= 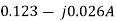
Q4) Estimate the currents for the circuit in figure using nodal analysis.
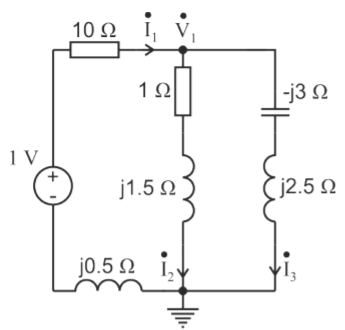
A4) 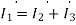 =
= 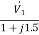 +
+ 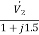
The node voltage then becomes
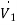 =
= 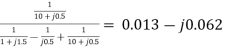
The value of currents will be
 =
= 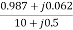 =
= 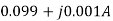
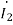 =
= 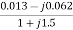 =
= 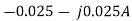
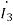 =
= 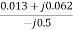 =
= 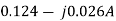
Q5) Estimate the currents for the circuit in figure using mesh analysis.
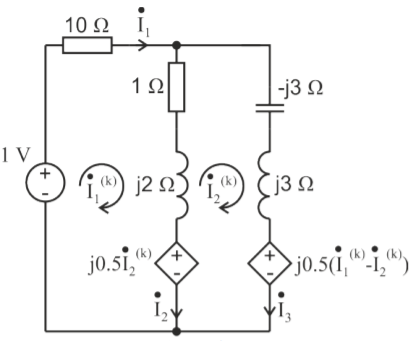
A5) First, we should estimate the branch currents with the mesh current

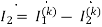

1-j0.5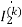 =
=  (10+1+j2)
(10+1+j2) 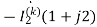
1=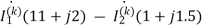
J0.5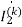 -j0.5
-j0.5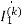 +j0.5
+j0.5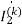 =
=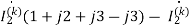 (1+j2)
(1+j2)
-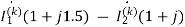

The determinants are
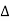 =
= 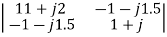 = 10.25+j10
= 10.25+j10
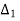 =
=  = 1+j
= 1+j
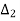 =
=  = 1+j1.5
= 1+j1.5
The value of currents will be
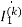 =
= 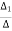 =
=  =
= 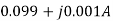
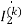 =
=  =
= 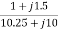 =
= 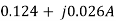
The value of branch current will now be
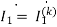 =0.099+j0.001A
=0.099+j0.001A
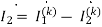 = 0.099+j0.001-0.123-j0.026=-0.024-j0.025A
= 0.099+j0.001-0.123-j0.026=-0.024-j0.025A
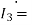 0.123+j0.026A
0.123+j0.026A
Q6) Find 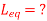

A6)
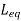 = 2H + 3H +10H - 2(10H)+ 2(4H) + 2(6H)
= 2H + 3H +10H - 2(10H)+ 2(4H) + 2(6H)
= 15H + - 20H + 20H
= 0
Q7) Find 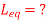
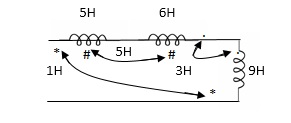
A7)
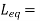 5H + 6H + 9H - 2(1H) -2(5H) -2(3H)
5H + 6H + 9H - 2(1H) -2(5H) -2(3H)
= 2H
Q8) A 25 KVA transformer has 500 turns on primary and 50 on secondary. The primary is connected to 2000V, 50 Hz supply. Find full load primary and secondary currents, the secondary emf and max flux in core. Neglect leakage drop and no load primary current.
A8) K = N2/N1 = 50/500 = 1/10
I1 = 25,000/2000 = 12.5 A
I2 = I1/K = 10 x 12.5 A = 125 A
Emf/turn on primary side = 2000/500 = 4 V
E2 = KE1
E2 = 4 x 50 = 200 v
E1 = 4.44fN1 Φm
2000 = 4.44 x 50 x 500 x Φm
Φm = 18.02 m Wb
Q9) In a 50 KVA, 2200/200 V, 1-φ transformer, the iron and full-load copper losses are 400 W and 450 W respectively. Calculate n at unity power factor on (i). Full load (ii). Half-full load?
A9) (i). Total loss = 400 + 450 = 850 W
F.L output at unity power factor = 50 x 1
= 50 KVA
n = 50 / 50 + .850 = 50/50.850 = 0.98 = 98%
(ii). Half full load, unity pf
= 50 KVA/2 = 25 KVA
Cu loss = 400 x (1/2)2 = 100 W
Iron loss is same = 450 W
Total loss = 100 + 450 = 550 W
n = 25/25 + 0.55 = 25/25.55 = 0.978 = 97.8 %
Q10) A 40 KVA 440/220 V, 1- φ, 50 Hz transformer has iron loss of 300 W. The cu loss is found to be 100 W when delivering half full-load current. Determine (i) n when delivering full load current at 0.8 lagging pf (ii) the percentage of full-load when the efficiency will be max.
A10) Full load efficiency at 0.8 pf
= 40 x 0.8/(40 x 0.8) + losses
Full load cu loss = (440/220)2 x 100
= 400 W
Iron loss = 400 + 300
= 700 W
n = 40 x 0.8/(40 x 0.8) + 0.7 = 97.8 %
(ii). KVA for maximum / F.L KVA = √ iron loss / F.L cu loss
= √300/400 = 0.866
Q11) Two transformers are required for a Scott connection operating from 410 V 3-Ø supply for supplying two 1-Ø furnaces at 200 V on the two-phase side. If total output is 130 kVA, calculate secondary to primary turn ratio and the winding of each transformer?
A11) For main Transformer
Primary voltage = 410 V
Secondary voltage = 200 V
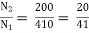
Secondary current = 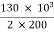 = 325 A
= 325 A
Primary current = 325 × 
= 153.54 A
For teaser Transformer
Primary volts = 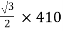 = 355 V
= 355 V
Secondary volts = 200 V
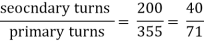
Q12) A delta-delta bank consisting of three 10kVA,2200/220v transformer supplies a load of 40kVA. If one transformer is removed, find the resulting V-V connection. Find total kVA rating of V-V bank and ratio of V-V bank to delta-delta transformer rating?
A12) kVA rating of V-V bank = 2x10x0.866 = 17.32kVA
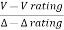 =
= 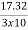 = 0.577 = 57.7%
= 0.577 = 57.7%
Q13) A delta-delta bank consisting of three 10kVA,2200/220v transformer supplies a load of 40kVA. If one transformer is removed, find the resulting V-V connection. a) kVA load carried by each transformer b)% of rated load carried by each transformer.
A13) As we already know  =
= 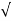 3
3
KVA load supplied by each transformer = 40/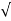 3 = 23.1kVA
3 = 23.1kVA
% of rated load = 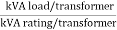 = 23.1/10 = 231 %
= 23.1/10 = 231 %
Q14) Two transformer connected in open delta supply a 430kVA balanced load operating at 0.9 p.f lagging. The load voltage is 460v. What is the kVA supplied by each transformer?
A14) kVA of each transformer = (430/2)/0.9 = 238.9kVA
The p.f of two transformers will be cos (30 -φ) and cos(30
-φ) and cos(30 +φ)
+φ)
Cos φ=0.9
φ = 25.8
P1= kVA cos (30 -φ) = 238.9 x cos (30
-φ) = 238.9 x cos (30 -25.8
-25.8 ) = 238.27kW
) = 238.27kW
P2= kVA cos (30 +φ) = 238.9 x cos (30
+φ) = 238.9 x cos (30 + 25.8
+ 25.8 ) =134.28kW
) =134.28kW
Q15) Two, 1-Φ furnaces working at 110v are connected to 3000v, 3-Φ mains through Scott connected transformer. Calculate the line current in 3-Φ mains when the power taken by each furnace is 400 kW at a p.f of 0.8 lagging. Transformer has no losses.
A15) K= 110/3000 = 0.0367
I2=400000/0.8x110 = 4545.5A
The 3-phase side is balanced as the load is balanced.
The primary phase current = 1.15kI2 = 1.15 x 0.0367 x 4545.5=191.84A
For star connection Iph=IL
IL= 191.84A
Q16) Two 1-Ø transformers, one of 800 kVA and 400 kVA are connected in parallel to the same bus bars on primary side. Their no load secondary voltage 500 V and 510 V respectively. The impedance voltage of first is 8% and that of second is 5%. Assume ratio of resistance to reactance is same and equal to 0.4 in each. Calculate the cross current when secondary’s are connected in parallel?
A16) The X/R is same for both; hence they do not have any phase difference.
Let secondary be 480 V
For full load IA = 800 × 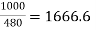 A
A
IB = 400 ×  A
A
ZA = 
ZB = 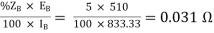
The cross current is given as
IC = 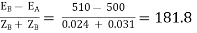 A
A
Q17) A coil takes a current of 6A when connected to 24V dc supply. To obtain the same current with 50HZ ac, the voltage required was 30V. Calculate inductance and p.f of coil?
A17) The coil will offer only resistance to dc voltage and impedance to ac voltage
R =24/6 = 4ohm
Z= 30/6 = 5ohm
XL = 
= 3ohm
Cosφ =  = 4/5 = 0.8 lagging
= 4/5 = 0.8 lagging
Q18) The potential difference measured across a coil is 4.5V, when it carries a dc current of 8A. The same coil when carries ac current of 8A at 25Hz, the potential difference is 24V. Find current and power when supplied by 50V,50Hz supply?
A18) R=V/I= 4.5/8 = 0.56ohm
At 25Hz Z= V/I=24/8 =3ohm
XL = 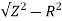
= 2.93ohm
XL = 2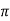 fL = 2
fL = 2 x 25x L = 2.93
x 25x L = 2.93
L=0.0187ohm
At 50Hz
XL = 2x3 =6ohm
Z = 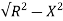 = 5.97ohm
= 5.97ohm
I= 50/5.97 = 8.37A
Power = I2R = 39.28W
Q19) A coil having inductance of 50mH an resistance 10ohmis connected in series with a 25 F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
A19) f0=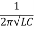 = 142.3Hz
= 142.3Hz
I0 = V/R = 200/10 = 20A
Q20) A 15mH inductor is in series with a parallel combination of 80ohm resistor and 20 F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
A20) XL = 2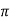 fL = 1000x15x10-3 = 15ohm
fL = 1000x15x10-3 = 15ohm
XL = 1/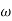 C = 50ohm
C = 50ohm
Impedance of parallel combination Z = 80||-j50 = 22.5-j36
Total impedance = j15+22.5-j36 = 22.5-j21
Admittance Y= 1/Z = 0.023-j0.022 siemens
Q21) A circuit connected to a 100V, 50 Hz supply takes 0.8A at a p.f of 0.3 lagging. Calculate the resistance and inductance of the circuit when connected in series and parallel?
A21) For series Z =100/0.8 = 125ohm
Cosφ = 
R = 0.3 x 125 = 37.5ohm
XL =  = 119.2ohm
= 119.2ohm
XL = 2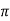 fL = 2
fL = 2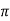 x 50x L
x 50x L
119.2 = 2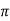 x 50x L
x 50x L
L= 0.38H
For parallel:
Active component of current = 0.8 cosφ = 0.3x0.3 = 0.24A
R = 100/0.24 =416.7ohm
Quadrature component of current = 0.8 sinφ = 0.763
XL= 100/0.763 = 131.06ohm
L= 100/0.763x2 x50 = 0.417H
x50 = 0.417H
Q22) For a series RLC circuit having R=10ohms, L= 0.15H, C=100 F. They are connected across 100v 50Hz supply. Calculate total impedance?
F. They are connected across 100v 50Hz supply. Calculate total impedance?
A22)
Impedance Z= 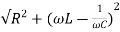
Z= 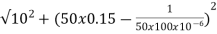 = 18.27ohm
= 18.27ohm
Q23) For a series RLC circuit having R=12ohms, L= 0.2H, C=60 F. They are connected across 100v 50Hz supply. Calculate circuit current?
F. They are connected across 100v 50Hz supply. Calculate circuit current?
A23)
I= 
Z= 
Z=  = 13.89ohm
= 13.89ohm
I = 100/13.89 =7.2A
Q24) For a series RLC circuit having R=10ohms, L= 0.15H, C=100 F. They are connected across 100v 50Hz supply. Calculate power factor?
F. They are connected across 100v 50Hz supply. Calculate power factor?
A24) cosφ = 
Impedance Z= 
Z= 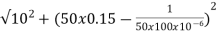 = 18.27ohm
= 18.27ohm
Cosφ =  =
= 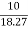
φ = 56.81o lagging