Unit - 3

Graph Theory

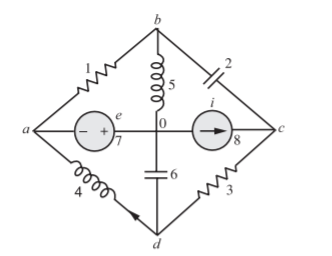
Q1) Draw the graph, one tree and its co-tree for the circuit shown in the figure?

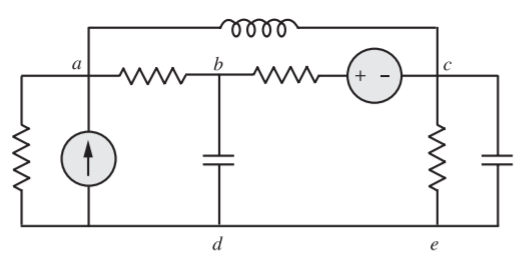
A1) We find that there are four nodes (N = 4) and seven branches (B = 7). The graph is then drawn and appears as shown in Figure below. It may be noted that node d represented in the graph represents both the nodes d and e.

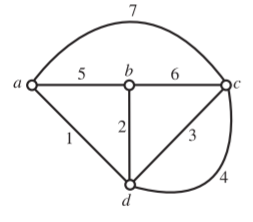
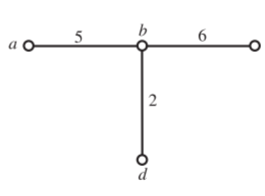
Fig Graph                                                        Fig Tree

Figure below shows one tree of graph shown in Figure above. The tree is made up of branches 2, 5 and 6. The co-tree for the tree of Figure above is shown below.

The co-tree has L = B − N +1=7 − 4+1=4 links.

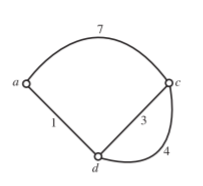
Fig Co Tree

Q2) Obtain the corresponding incidence matrix for the circuit shown in following figure?

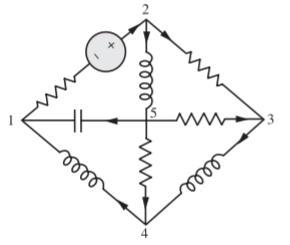
A2) The network shown above has 5 nodes and 8 branches. The corresponding graph appears in the following figure.

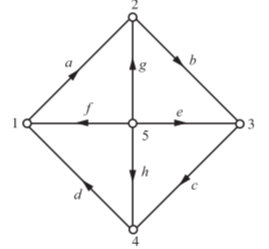
The incidence matrix is formed by following the rule:

The entry of the incidence matrix,

ak = 1, if the current of branch k leaves the node i

= 1, if the current of branch enters node i

= 0, if the branch k is not connected with node i

Incident Matrix

In matrix form we write it as

A5 =

Where subscript 5 indicates that there are five nodes in the graph. It may be noted that from a given incidence matrix, the corresponding graph can be drawn.

Q3) For the incidence matrix shown below, draw the graph?

A3) Observing the matrix, it can be seen that it is a reduced incidence matrix. Branches 1, 2, 3 and 4 are to be connected to the reference node. Branch 5 appears between the nodes a and b, 6 between b and c, 7 between c and d, 8 between a and c. With this information, the oriented graph is drawn as shown below. Orientation is +1 for an arrow leaving a node d -1 for an arrow entering a node.

Q4) Draw the graph of a network of whose incidence matrix is

A4) Sum of the elements in columns 4, 9 are not zero. Therefore, the given matrix is a reduced matrix. Taking 0 as reference node, the oriented graph is as shown in Figure after making the nodes in an order.

Q5) For the graph shown in Figure, write the incidence matrix. Express branch voltage in terms of node voltages and then write a loop matrix and express branch currents in terms of loop currents.

A5) With the orientation shown in Figure above, the incidence matrix is prepared as shown below

Branch voltages in terms of node voltages are

V1=ec-ed

V2=eb-ed

For loop (tie-set) matrix,

L= B-N+1=8- 5+1=4.

With twigs (1, 2, 3, 4), we have chords (links) (5, 6, 7, 8) and the corresponding tree is as shown in Fig. Introducing the chords one at a time, the tie-set matrix is prepared as below

The branch currents in terms of loop currents are J1 = −i1 − i4, J2 = i1 − i2 etc.

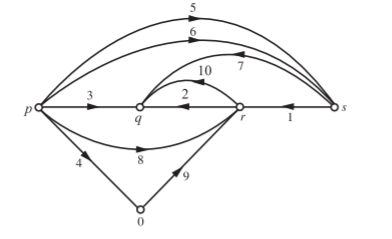
Q6) For the network shown below, determine the number of all possible trees. For a tree consisting of (1, 2, 3) (i) draw tie set matrix (ii) draw cut-set matrix.

A6) If the intention is to draw a tree only for the purpose of tie-set and cut-set matrices, the ideal current source is open circuited and ideal voltage source is short circuited. The oriented graph is drawn for which d is the reference.

A=

Det AAT = + = 12

Therefore, possible number of trees = 12

The corresponding graph, tree, co-tree, and loops 1, 2, 3 are shown below

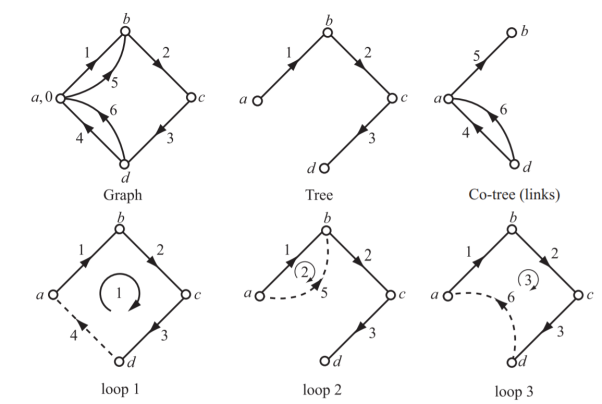
(i) Tie-set matrix for twigs (1, 2, 3) is

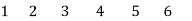
(ii) Cut-set matrix is

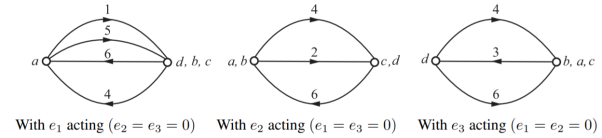
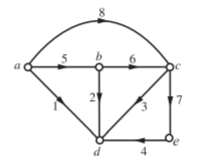
Q7) For the circuit shown below, write a tie-set schedule and then find all the branch currents and voltages?

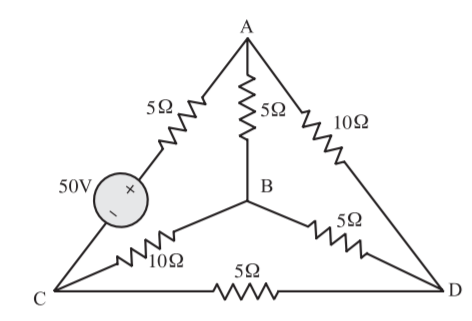
A7) Figure below shows the graph for the network. Also, a possible tree and co-tree are shown in Fig. Co-tree is in dotted.

First, the tie-set schedule is formed and then the tie-set matrix is obtained.

Tie-set matrix is

M=

The branch impedance matrix is

ZB =

EB =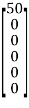

The loop impedance matrix is

ZL = MZBMT

ZL= +

ZL= + =

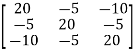
MEB=

The loop equations are obtained using the equation

ZLIL= MEB

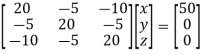
x=4.1666A

y=1.1666A

z=2.5A

The branch currents are computed using the equations

IB=MTIL

I1 = x = 4.1666 A, I2 = y = 1.6666 A, I3 = z = 2.5 A, I4 = x − z = 1.6666 A, I5 = −x + y = −2.5 A, I6 = −y + z = 0.8334 A

The branch voltages are computed using the equation

VB = ZBIB − EB

= -

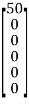
Hence, V1 = 5I1 − 50 = 29.167 V,

V2 = 10I2 = 16.666 V

V3 = 5I3 = 12.50 V

V4 = 10I4 = 16.666 V

V5 = 5I5 = −12.50 V

V6 = 5I6 = 4.167 V

Q8) Find the tie-set matrix and loop currents for the circuit shown below

A8) In the circuit, 4 Ω in series with current source is shorted (as it is trivial), the graph is as shown in Figure with 1 as tree branch and 2 as link.

Using the equation, MZBMTIL = MEB − MZBIB with M = [1 1], we have

MZBMT = 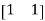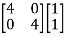=8

MEB − ZBIB = (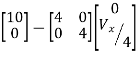) =10-Vx

8I1 = 10 − Vx

But Vx = 4I1

8I1 = 10 − 4I1

I1 = 5/6A

As I1 = Vx/4 − I2

I2 = 5/6A

Q9) For the given cut-set matrix, draw the oriented graph

A9) Data from the matrix: B = 7, Nt = 5, N = 4, L = 3. Tree branch voltages are e1 = v1, e2 = v2, e3 = v3 and e4 = v4. Therefore, all these are connected to reference node. Individual cut-sets are

Which indicates that 5 is common to a and b, 7 is common to b and c, 6 is common to c and d.

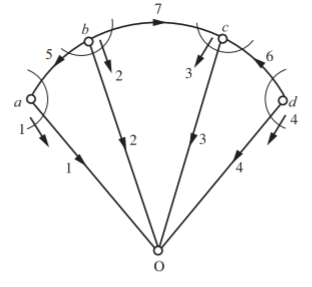
Q10) Solve for branch currents and branch voltages.

A10) The oriented graph for the network is shown below. A possible tree and cotree with fundamental cut-sets are as shown.

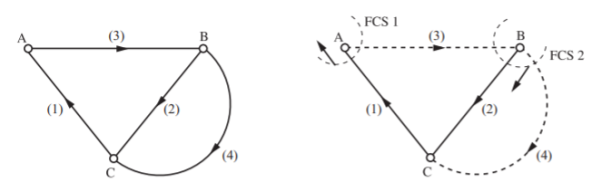
Cut Set

Cut-set matrix:

Q =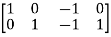

Branch admittance matrix:

YB =

Cut-set admittance matrix:

YN = QYBQT

YN=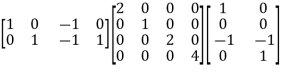

YN=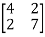

Equilibrium equations: YN EN = QIB

=

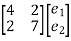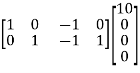
e1= -70/24V

e2= 20/24V

Branch voltage are found using the matrix equation: VB= QTEN

=

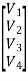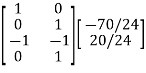
V1= -2.91V

V2= 0.833V

V3= 2.084V

V4= 0.833V

Branch currents are found using the matrix equation JB= YBVB−IB

=

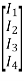I1= 4.166A

I2 = 0.833A

I3= 4.168V

I4= 3.333V

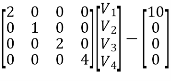
Q11) For the oriented graph shown, express loop currents in terms of branch currents for an independent set of columns as those pertinent to the links of a tree:

(i) Composed of 5, 6, 7, 8

(ii) Composed of 1, 2, 3, 6

Verify whether the two sets of relations for i’s in tems of j’s are equivalent. Construct a tie-set schedule with the currents in the links 4, 5, 7, 8 as loop currents and find the corresponding set of closed paths

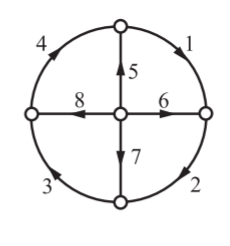
A11) For first set

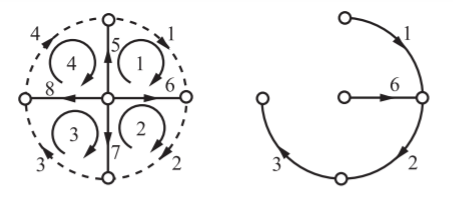
B=5,6,7,8

L=1,2,3,4

Then for second set of the mesh currents indicated for the first set we have

J4=i4

J5=i1-i4

J7=i3-i2

J8=i4-i3

By applying KCL we have

i1=J1=J4+J5

i2=J2=J3-J7

i3=J3=J4-J8

i4=J4

Thus, the two sets of relations for i’s in terms of J’s are equivalent. The tie-set schedule with the currents in links 4, 5, 7, 8 as loop currents.

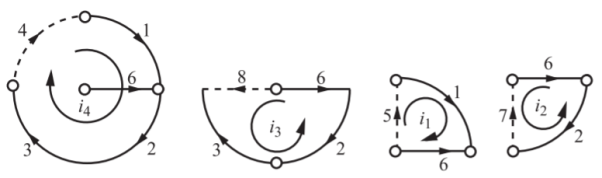
Q12) In the graph shown in Figure, the ideal voltage source e = 1 V. For the remaining branches each has a resistance of 1 Ω with O as the reference. Obtain the node voltage e1, e2 and e3 using network topology.

A12)

Q13) For the circuit shown in Figure, for a tree consisting of ab, bc, cd form a tie-set schedule and obtain equilibrium loop equations. Choose branch numbers same as their resistance values. Solve for loop currents

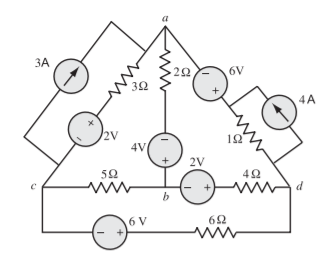
A13) The oriented graph is

Tree with nodes ab, bc, cd and links are shown in line. The tie set matrix is

Q14) For the network shown in Figure, prepare a cut-set schedule and obtain equilibrium equations. Number the branches by their ohmic values.

A14) Numbering the branches same as those of ohmic values, the oriented graph is as shown in Figure. Choosing 4, 5, 6 as tree branches, the tie set schedule is as shown below

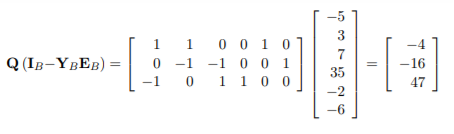
Q15) Device a tree for the circuit shown in Figure, for which all the currents pass through 1 Ω. For this tree write the tie-set matrix to obtain equilibrium equations.

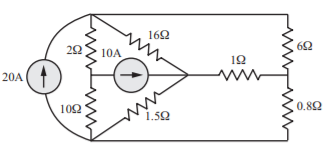
A15) The network can be re drawn as shown below

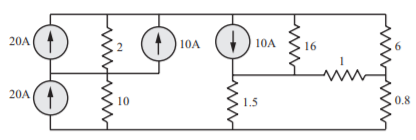
Q16) For the circuit shown in Figure, construct a tree in which v1 and v2 are tree branch voltages, write a cut-set matrix and obtain equilibrium equations. Solve for v1

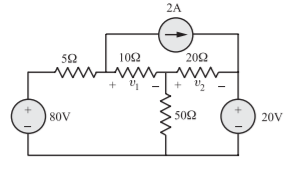
A16) The circuit can be redrawn as

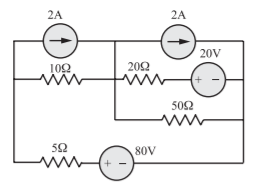
With v1 and v2 as tree branch voltages the graph is as shown in Figure, with tree branches with full lines and the links in dotted line

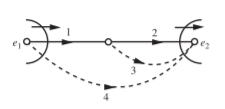
Q17) (a) Construct a tree for the circuit shown in Figure so that i1 is a link current. Assign a complete set of link currents and find i1(t).

(b) Construct another tree in which v1 is a tree branch voltage. Assign a complete set of tree branch voltages and find v1(t)v. Take i(t) = 25 sin 103t Amp, v(t) = 15 cos 103(t)

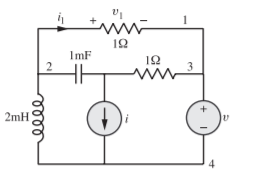
A17) (a) The circuit after I shift is as shown in Fig.

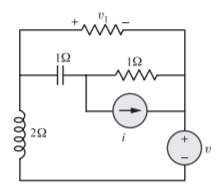
The oriented graph is as shown below. With branches as numbered, and 1 as a link the tree is as shown. Links are shown in dotted line (links are 1 and 4). The tie-set matrix is

Q18) Define the terms Graph, Branch, Loop, Mesh, Planar graph and oriented graph?

A18) The description of networks in terms of their geometry is referred to as network topology. The adequacy of a set of equations for analysing a network is more easily determined topologically than algebraically.

Graph (or linear graph): A network graph is a network in which all nodes and loops are retained but its branches are represented by lines. The voltage sources are replaced by short circuits and current sources are replaced by open circuits. (Sources without internal impedances or admittances can also be treated in the same way because they can be shifted to other branches by E-shift and/or I-shift operations.)

Branch: A line segment replacing one or more network elements that are connected in series or parallel.

Node: Interconnection of two or more branches. It is a terminal of a branch. Usually, interconnections of three or more branches are nodes. Path: A set of branches that may be traversed in an order without passing through the same node more than once.

Loop: Any closed contour selected in a graph.

Mesh: A loop which does not contain any other loop within it.

Planar graph: A graph which may be drawn on a plane surface in such a way that no branch passes over any other branch. Non-planar graph: Any graph which is not planar.

Oriented graph: When a direction to each branch of a graph is assigned, the resulting graph is called an oriented graph or a directed graph.

Q19) Describe tree branch voltage with any example and also derive relation between link, node and branch?

A19) Tree branch voltages: The branch voltages may be separated in to tree branch voltages and link voltages. The tree branches connect all the nodes. Therefore, if the tree branch voltages are forced to be zero, then all the node potentials become coincident and hence all branch voltages are forced to be zero. As the act of setting only the tree branch voltages to zero forces all voltages in the network to be zero, it must be possible to express all the link voltages uniquely in terms of tree branch voltages. Thus, tree branch forms an independent set of equations.

Cut set: A set of elements of the graph that dissociates it into two main portions of a network such that replacing any one element will destroy this property. It is a set of branches that if removed divides a connected graph in to two connected sub-graphs. Each cut set contains one tree branch and the remaining being links.

Node, Link and Brach Relation

Let B = Total number of branches in the graph or network

N = total nodes

L = link branches

Then N − 1 branches are required to construct a tree because the first branch chosen connects two nodes and each additional branch includes one more node.

Number of independent node pair voltages = N − 1 = number of tree branches.

Then L = B − (N − 1) = B − N + 1

Number of independent loops = B − N + 1

Q20) Taking any example explain tie set matrix with step by step procedure for constructing the matrix?

A20) From the knowledge of the basic loops (tie-sets), we can obtain loop matrix. In this matrix, the loop orientation is to be the same as the corresponding link direction. In order to construct this matrix, the following procedure is to be followed.

1. Draw the oriented graph of the network. Choose a tree.

2. Each link forms an independent loop. The direction of this loop is same as that of the corresponding link. Choose each link in turn.

3. Prepare the tie-set matrix with elements bij.

Where bij = 1, when branch bj in loop i and is directed in the same direction as the loop current.

bij=-1, when branch bj in loop i and is directed in the opposite direction as the loop current.

bij=0, when branch bj is not in loop i.

Tie-set matrix is an i x b matrix

For example, let us consider

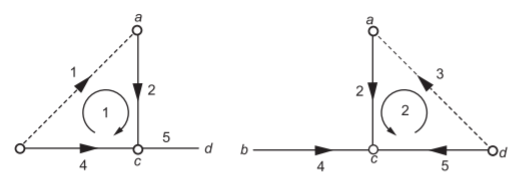
Selecting (2, 4, 5) as tree, the co-tree is (1, 3). The tie set will now be

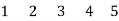
A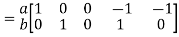 = At; Ai

VB =  

Then MVB gives the following independent loop equations: v1 + v2-v4 = 0

v2 + v3-v5=0

= 0 Looking column wise, we can express branch currents in terms of loop currents. This is done by the following matrix equation as

JB=MTIL

The above matrix equation gives

J1=i1

J2=i1+i2

J3=i2

J4=-i1-i2

Note that J stands for branch current while i stands for loop current. In this matrix

(i)                Each row corresponds to an independent loop. Therefore, the columns of the resulting schedule automatically yield a set of equations relating each branch current to the loop currents.

(ii)              (ii) As each column expresses a branch current in terms of loop currents, the rows of the matrix automatically yield the closed paths in which the associated loop currents circulate. Expressions for branch currents in terms of loop currents may be obtained in matrix form as JB=MTIL

M is the Tie Set Matrix of L x B