Unit - 6
State Space Analysis
Q1) Obtatin the state space representation for the given electrical system
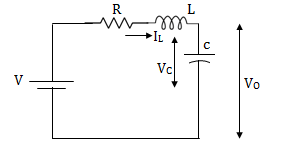
A1)
The state model is given as
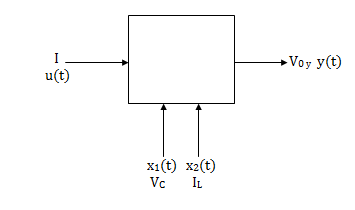
The state model shows that there are two energy storing elements L, C. As we already know that Number of state variables is equal to the number of energy storing elements.Hence we have two state variables[x1(t) and x2(t)]. We have one output V0(taken across capacitor) and input u(t).
The output equation is then given as
Y(t)=CX(t)+DU(t)
V0=Vc= x1(t) ….(a)
Hence output equation becomes
V0= x1(t)
y(t)=[1 0]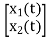 +[0]u(t)
+[0]u(t)
So, C=[1 0] D=[0]
Now writing the state equation
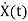 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
For that applying KVL in the above circuit
V=ILR+L +Vc
+Vc
State Equation is  =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
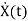 =
=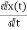
x1(t)=Vc
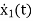 =
=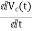
IL=C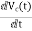
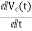 =
=
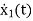 =
= =
=
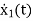 =(1/C) x2(t) ……….(b)
=(1/C) x2(t) ……….(b)
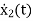 =
=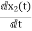 =
=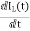
VL=L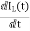
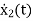 =
=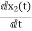 =VL/L
=VL/L
From KVL
L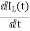 =VL=V-ILR-VC
=VL=V-ILR-VC
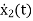 =
=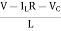 =
=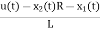
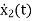 =
= …………….(c)
…………….(c)
From equation (b) and (c)
 = [0 1/c]
= [0 1/c]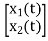 + [0 0] u(t)
+ [0 0] u(t)
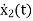 =[-1/L -R/L]
=[-1/L -R/L]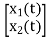 + [1/L 0]
+ [1/L 0]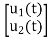
Now writing the state equation
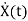 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
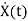 =
=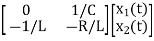 +
+ 
Hence A=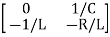 B=
B= 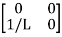
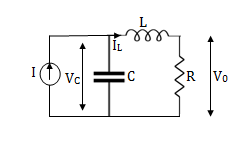
Q2) Obtatin the state space representation for the given electircal system
A2)
The state model shows that there are two energy storing elements L, C. As we already know that Number of state variables is equal to the number of energy storing elements.Hence we have two state variables[x1(t) and x2(t)]. We have one output V0(taken across capacitor) and input u(t).
Here output is V0. But from above electrical circuit V0=ILR
V0=x2(t)R
y(t)= V0= [0 R] 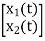 + [0] u(t)
+ [0] u(t)
The output equation is given as
Y(t)=CX(t)+DU(t)
C=[0 R] D=[0]
Now finding state equation,we apply KCL in the given electrical circuit
I=IC+IL
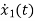 =
=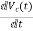
But I-IL=IC
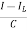 =
=
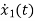 =
=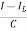
 =
=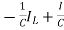
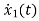 =
=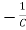 x2(t)+
x2(t)+ ……..(a)
……..(a)
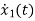 =[0 1/C]
=[0 1/C]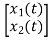 + [1/C 0]
+ [1/C 0]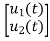 …….(b)
…….(b)
 =
=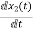 =
=
Applying KVL in the given electrical circuit we get
VC=VL+ILR
VC-ILR=VL=L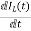
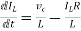
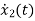 =
=
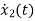 = [1/L -R/L]
= [1/L -R/L] 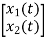 + [0] u(t) …………. (c)
+ [0] u(t) …………. (c)
From equation (b) and (c) we have
Now writing the state equation
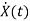 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
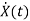 =
=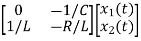 +
+ 
Hence A= B=
B= 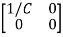
Note: We should always take voltage across the inductor L, and current through capacitor C.
Q3) Write the state equation for the mechanical system shown below?
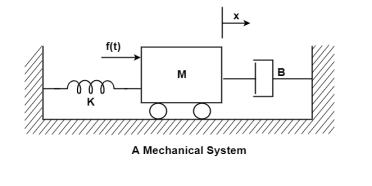
A3)
The free body diagram is
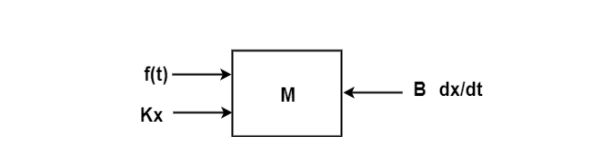
The position and velocity are state variables hence,
x1(t)=x(t)
x2(t)= 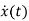
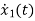 =
=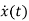 =x2(t)
=x2(t)
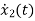 =
=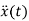
The system equation will be
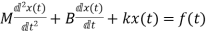
 =
=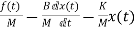
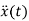 =
=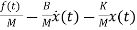
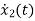 =
=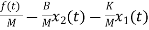
The state equations are
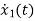 = x2(t)
= x2(t)
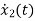 =
=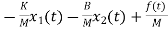
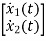 =
=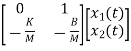 +
+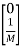 f(t)
f(t)
Q4) The closed loop transfer function is given as T(s)=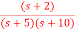 . Calculate the state model?
. Calculate the state model?
A4)
The transfer function can be simplified using partial fraction method as
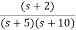 =
=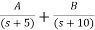
S+2=As+10A+Bs+5B
Equating coefficients of s from both sides
A+B=1
Equating coefficients of s0 from both sides
10A+5B=2
Solving above equations we get
A=-3/5
B=8/5
The transfer function will be
T(s)=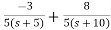
=-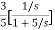 +
+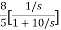
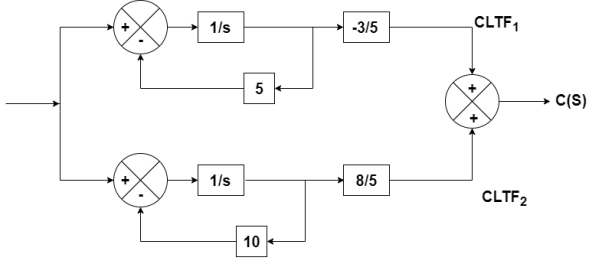
Number of poles= Number of energy storing elements
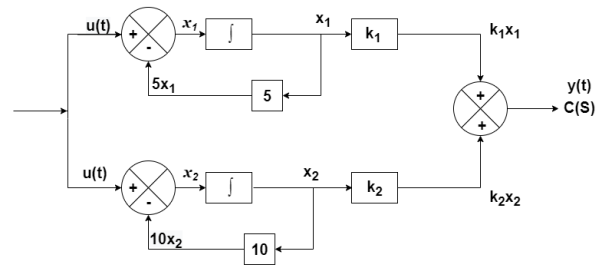
The output equation is given as
y(t)=k1x1(t)+k2x2(t)
y(t)= [k1 k2]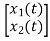 + [0] [u(t)]
+ [0] [u(t)]
y(t)= [-3/5 8/5]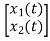 + [0] [u(t)]
+ [0] [u(t)]
C= [-3/5 8/5]
D=0
From the above block diagram
 =u(t)-5 x1
=u(t)-5 x1
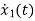 =-5x1+u(t)
=-5x1+u(t)
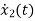 =-10x2+u
=-10x2+u
Therefore, the state equation is given as
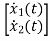 =
=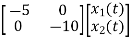 +
+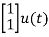
A=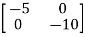
B=
Q5) The closed loop transfer function is given as T(s)=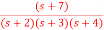 . Calculate the state model?
. Calculate the state model?
A5)
The transfer function can be simplified using partial fraction method as
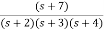 =
= +
+ 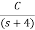
s+7=A[s2+7s+12] +B[s2+6s+8] +C[s2+5s+6]
Equating coefficients of s2 from both sides
A+B+C=0
Equating coefficients of s from both sides
7A+6B+5C=1
Equating coefficients of s0 from both sides
12A+8B+6C=7
Solving above equations and finding values of A, B and C
A=5/2
B=-4
C=3/2
The transfer function will be
T(s)=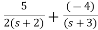 +
+ 
=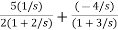 +
+ 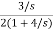
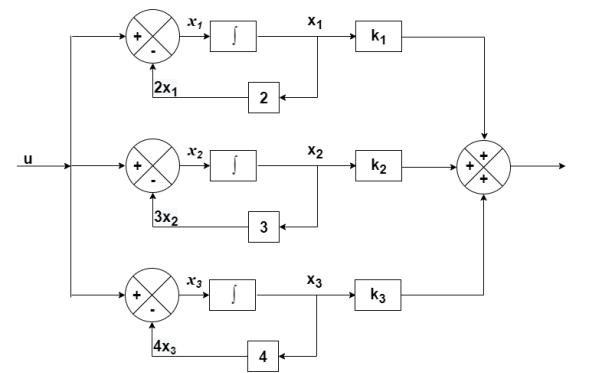
The output equation will be
y=k1x1+k2x2+k3x3
y= [k1 k2 k3] [5/2 -4 3/2]
[5/2 -4 3/2]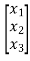
C= [5/2 -4 3/2]
D= [0]
The state equation is given as
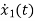 =u(t)-2x1
=u(t)-2x1
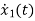 =-2x1+u(t)
=-2x1+u(t)
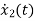 =-3x2+u
=-3x2+u
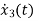 = -4x3+u
= -4x3+u
Therefore
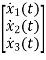 =
=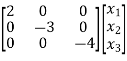 +
+ [u]
[u]
A=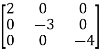
B=
Q6) The closed loop transfer function is T(s)=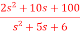 . Find the state equation?
. Find the state equation?
A6)
Here the number of poles = number of zeros
T(s)=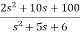
=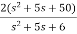
=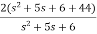
=2+ 
=2+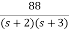
Solving above by partial fraction method
88= As+2A+Bs+3B
A=-B
2A+3B=88
A=-88
B=88
The transfer function becomes
T(s)= 2-
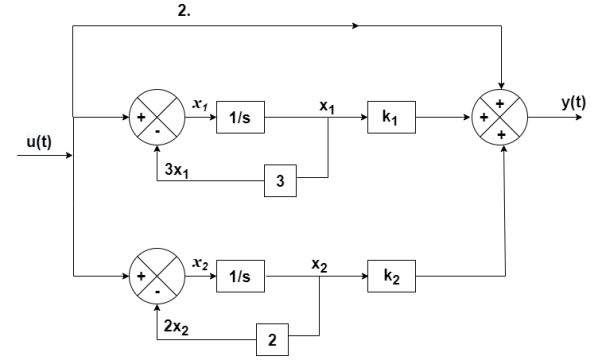
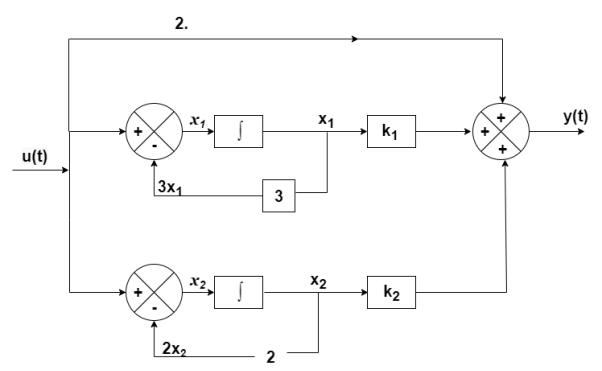
The output equation will be
y(t)=2U+k1x1+k2x2
y= [-88 88]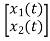 + [2]u
+ [2]u
The output equation will be
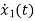 =u(t)-3 x1
=u(t)-3 x1
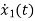 =-3x1+u(t)
=-3x1+u(t)
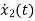 =-2x2+u(t)
=-2x2+u(t)
Therefore, the state equation is given as
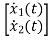 =
=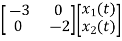 +
+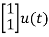
A=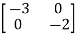
B=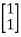
Q7) The CLTF T(s)=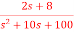 . Find the state equation?
. Find the state equation?
A7)
T(s)=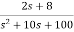
=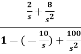
P1=2/s
P2=-8/s2
L1=-10/s
L2=-100/s2
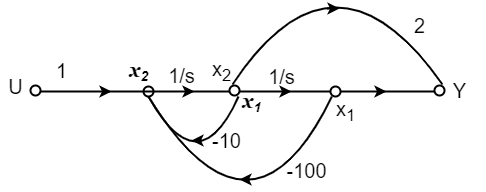
The state equation will be
 =x2
=x2
 =-10x2-100x1+u
=-10x2-100x1+u
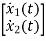 =
=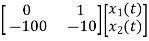 +
+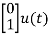
Q8) Find the state equation from the given differential equation
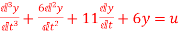
A8)
Let y=x1
 =
= =x2
=x2
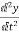 =
=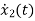 =x3
=x3
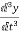 =
=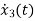
The above differential equation than becomes
 +6
+6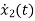 +11 x2+6 x1=u
+11 x2+6 x1=u
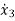 (t) =u-6
(t) =u-6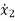 (t)-11 x2-6 x1
(t)-11 x2-6 x1
Hence the state equation will be
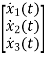 =
= 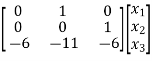 +
+ [u]
[u]
Q9) For the given data below compute the transfer function of the system
A=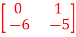 B=
B= C= [1 0] and D= [0]
C= [1 0] and D= [0]
A9)
The state equation will be
 =
=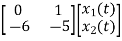 +
+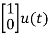
 =x1
=x1
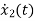 =-6x1-5x2
=-6x1-5x2
Equation (14) in section 4.1
 = C{[SI-A]-1B} + D
= C{[SI-A]-1B} + D
=C {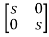 -
-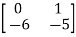 }-1B+D
}-1B+D
=C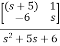 B+D
B+D
= [1 0] 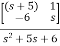
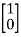 + 0
+ 0
=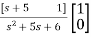 +0
+0
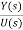 =
=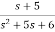
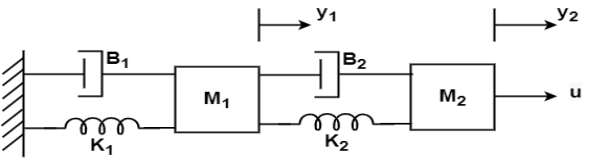
Q10) Obtain the state space representation of following mechanical system
A10)
The position and velocity state variables will be
x1=y1
x2=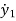
x3=y2
x4=
The difference equation will be
M1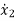 +B1
+B1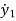 +K1y1+B2(
+K1y1+B2( -
-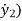 +K2(y1-y2) =0
+K2(y1-y2) =0
M2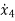 + K2(y2-y1) + B2(
+ K2(y2-y1) + B2( -
-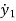 )=u
)=u
Writing above equations in the form of state variables
M2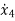 =u-K2(y2-y1) +-B2(
=u-K2(y2-y1) +-B2(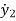 -
-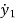 )
)
M1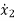 =- B1
=- B1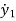 -K1y1-B2(
-K1y1-B2(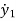 -
-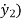 -K2(y1-y2)
-K2(y1-y2)
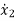 = -(
= -(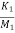 +
+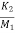 )x1- (
)x1- (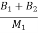 ) x2+(
) x2+(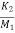 )x3+
)x3+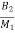 x4
x4
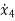 =
= 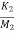 x1+
x1+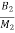 x2-
x2-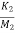 x3-
x3-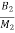 x4+
x4+
Now writing all the state equations
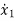 =x2
=x2
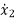 = -(
= -(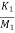 +
+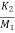 )x1- (
)x1- ( ) x2+(
) x2+(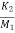 )x3+
)x3+ x4
x4
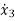 = x4
= x4
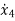 =
= 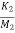 x1+
x1+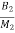 x2-
x2-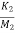 x3-
x3-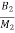 x4+
x4+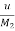
The matrix form for above equations is given below
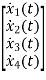 =
= 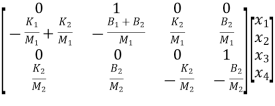 +
+ v(t)
v(t)
Q11) A system is described by  =
=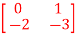 B=
B= C=[1 0] . Y = [1 0]. Check the controllability of the system?
C=[1 0] . Y = [1 0]. Check the controllability of the system?
A11)
[s] =[B AB]
= 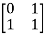
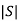 ≠ 0 hence system is controllable.
≠ 0 hence system is controllable.
Q12) A system is described by  =
=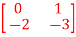 B=
B= C=[1 0] . Y = [1 0]. Check the observability of the system?
C=[1 0] . Y = [1 0]. Check the observability of the system?
A12)
AT=  CT=
CT=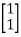
[Q]=[CT ATCT]
=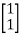
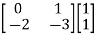
=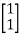
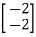
=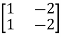
=0
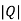 =0 hence not observable.
=0 hence not observable.
Q13) The state equation of the system is given below 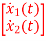 =
= 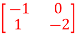
 +
+  u(t) . Y = [1 2]
u(t) . Y = [1 2] Comment on controllability?
Comment on controllability?
A13)
A= 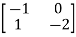 B=
B= 
Order of matrix n=2
[S] = [B AB]
=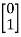
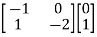
= 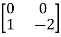
|S|= 0. Hence, system is not controllable.
Q14) The state space representation of a second order 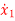 = -x1+u and
= -x1+u and  = x1-2x2+u. State whether the system is controllable or not?
= x1-2x2+u. State whether the system is controllable or not?
A14)
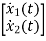 =
= 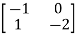
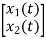 +
+ 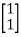 u(t)
u(t)
Order of matrix is n=2
[S] = [B AB]
=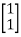
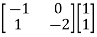
= 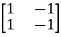
|S|= 0. Hence, system is not controllable.
Q15) A linear second order single input continuous time system is described as 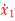 = -2x1(t)+4x2(t) and
= -2x1(t)+4x2(t) and 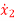 = 2x1(t)-x2(t)+u(t). Comment on controllability?
= 2x1(t)-x2(t)+u(t). Comment on controllability?
A15)
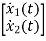 =
= 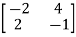
 +
+ 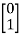 u(t)
u(t)
Order of matrix is n=2
[S] = [B AB]
=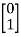
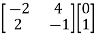
= 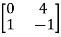
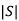 ≠ 0 hence system is controllable.
≠ 0 hence system is controllable.
Q16) Find the controllable canonical realization of the following systems H(s)=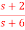
A16)
H(s)=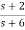
Let H(s)=
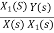 =
=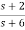
H1(s)=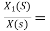 1/s+6
1/s+6
X(s)=sX1(s)+6X1(s)
SX1(s)= X(s) +6X1(s)
We can get X1(s) by passing sX1(s) through integrator. The above equation can be realised as
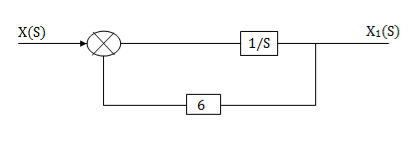
H2(s)=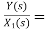 s+2
s+2
Similarly, Y(s)= sX1(s)+2X1(s)
H2(s)=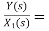 s+2
s+2
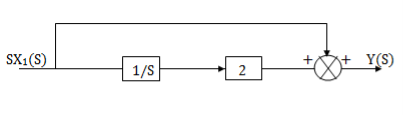
The complete realization of transfer function can be obtained by combining the above two realizations. The complete realization will be
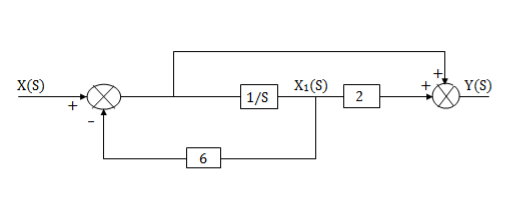
Q17) Find the controllable canonical realization of the following systems H(s)=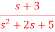
A17)
H(s)=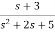
Let H(s)= =
= 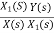
 =s+3
=s+3
Y(s)=sX1(s)+3X1(s)
The above transfer function can be realised as
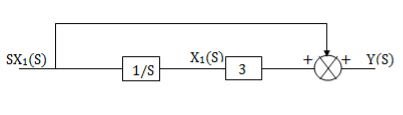
Now, 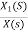 =
=
s2X1(s)=X(s)-2sX1(s)-5X1(s)
Assuming s2X1(s) is available the above transfer function can be realised as
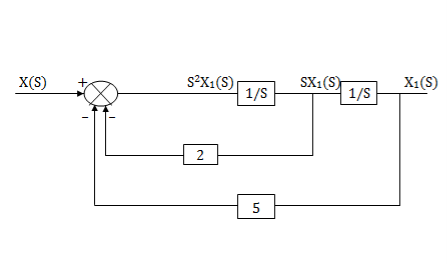
The complete realization of transfer function can be obtained by combining the above two realizations. The complete realization will be
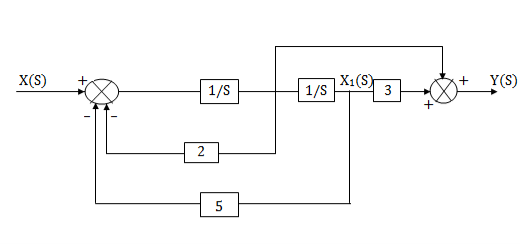
Q18) What is the effect of pole zero cancellation on the controllability and observability of the system?
A18)
For an nth order system with distinct eigenvalues the transfer function be
T(s)=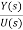 =[b0sm+b1sm-1+….+bm-1s+bm/[sn+a1sn-1+……..+an-1s+an]
=[b0sm+b1sm-1+….+bm-1s+bm/[sn+a1sn-1+……..+an-1s+an]
=K(s-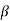 1)( s-
1)( s-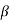 2)…….( s-
2)…….( s-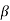 m)/(s-
m)/(s-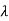 1)( s-
1)( s-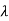 2)……( s-
2)……( s-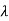 n)
n)
= 
ck are residue poles at s=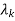
If the transfer function has identical pair of poles and zeros at 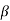 i=
i= 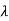 i
i
The effect of this cancellation of pole and zero on observability and controllability depends on the property of state variable.
- If the state variable is of the form below, then ci=0 will appear in control vector B and the state is uncontrollable.
 =
= 
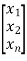 +
+  u
u
y=[1 1 1……..1] +b0u
+b0u
- On the other-hand if the state variables are of the form
 =
=  +
+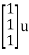
y=[c1 c2 c3…….. cn]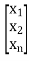 +b0u
+b0u
Then then ci=0 will appear in output vector C and the state is shielded from observations.
- In LTI system if it has pole zero cancellation, the system will either be not controllable nor observable. But if the transfer function does not have any pole zero cancellations than the system can be represented by completely controllable and observable state model.
Q19) Explain the concept of state variable?
A19) The state of a system is a minimal set of variables known as state variables. The knowledge of these variables at any instance of time together with the knowledge of the inputs for the same instance of time, determines the complete behaviour of the system. The fewer drawbacks in the transfer function method for representing any system led to the use of state variables in analysis of system. Few advantages are listed below:
- The state space can be used for linear or nonlinear, time-variant or time-invariant systems.
- It is easier to apply where Laplace transform cannot be applied.
- The nth order differential equation can be expressed as 'n' equation of first order.
- It is a time domain method.
- As this is time domain method, therefore this method is suitable for digital computer computation.
- On the basis of the given performance index, this system can be designed for an optimal condition.
Q20) Derive the state equation and output equation of a system?
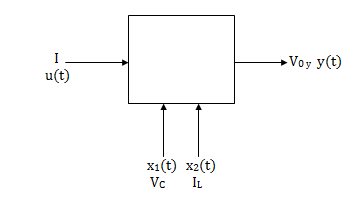
A20) Representation of state space: The system shown below has ‘m’ inputs, ‘p, outputs and ‘n’ number of state variables. The state equation gives us the relation between the state variables and the inputs.
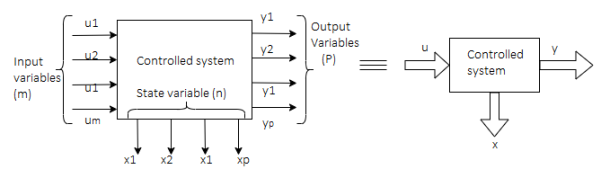
So, the above system shown can be described through equations as
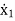 =f1 (x1, x2,…….xn , u1, u2……… ,um)
=f1 (x1, x2,…….xn , u1, u2……… ,um)
 = f2 (x1, x2,…….xn , u1, u2……… ,um)
= f2 (x1, x2,…….xn , u1, u2……… ,um)
….
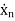 =f1 (x1, x2,…….xn , u1, u2……… ,um) (1)
=f1 (x1, x2,…….xn , u1, u2……… ,um) (1)
The above set of equations can be represented as
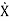 =f(x(t), u(t)) (2)
=f(x(t), u(t)) (2)
As we are concerned for time invariant system, for which the term 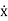 in (1) is linear combination of state variables and input. So,
in (1) is linear combination of state variables and input. So,
 (t)=2tx1+x2+u1+u2 (3)
(t)=2tx1+x2+u1+u2 (3)
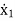 =a11x1(t)+a12x2(t)+…a1nxn(t)+b11u1(t)+b12u2(t)+……. +b1mum(t)
=a11x1(t)+a12x2(t)+…a1nxn(t)+b11u1(t)+b12u2(t)+……. +b1mum(t)
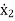 =a21x1(t)+a22x2(t)+…a2nxn(t)+b21u1(t)+b22u2(t)+……. +b2mum(t)
=a21x1(t)+a22x2(t)+…a2nxn(t)+b21u1(t)+b22u2(t)+……. +b2mum(t)
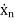 =an1x1(t)+an2x2(t)+…annxn(t)+bn1u1(t)+bn2u2(t)+……. +bnmum(t)
=an1x1(t)+an2x2(t)+…annxn(t)+bn1u1(t)+bn2u2(t)+……. +bnmum(t)
The above equation can be represented in matrix form as given below
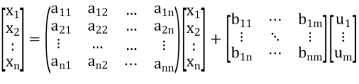 (4)
(4)
The above coefficients aij and bji in equation (4) can be written in vector matrix form as
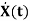 =Ax(t)+Bu(t) (5)
=Ax(t)+Bu(t) (5)
The output of the system can be represented by linear combination of state variables and inputs.
y1=c11x1(t)+c12x2(t)+……. +c1nxn+d11u1+………. +d1mum
y2=c21x1(t)+c22x2(t)+……. +c2nxn+d21u1+………. +d2mum
yr=cr1x1(t)+cr2x2(t)+……. +crnxn+dr1u1+………. +drmum (6)
The equation (6) can be represented in matrix form as
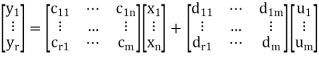 (7)
(7)
Where coefficients cij and dji are constants. The output equation is given as
Y=CX+DU (8)