Unit - 4
Laplace and z- Transforms
Q1) Find H(z), poles and zeros for the difference equation given by
y[n] – 3/8 y[n-1] – 7/16 y[n-2] = x[n] + x[n-2]
A1)
Here ao=1,a1=-3/8,a2=-7/6,bo=1,b1=0,b2=1
H[z] = 1 + z -2 / 1 -3/8 z-1 -7/16 z -2
= (1+j z-1 ) (1 -jz-1) / (1-7/8 z-1) ( 1+1/2 z-1)
Zeros : z=
j represented by o.
Poles z= 7/8 , z=-1/2 represented by x.
Figure 1. Poles and Zeros
Q2) Find the Laplace transform of e –t.
A2)
F(s) = 
F(s) =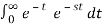 
F(s) = 
F(s) = 1 / 1-s [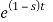
]0 
F (s = 1/ s-1.
Q3) Find the Laplace transform of unit -step function.
A3)
f(t) = 1 (t≥0)
F(s) = 
-st dt = -1/s e -st | 0 ∞ = 1/s [ e -∞ - e -0] = 1
F(s) = 1/s.
Q4) Find the Laplace transform of e-at u(t)
A4)
X(s) = 
at u(t) e -st dt = 
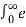at e -st dt = 
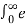–(s-a) t dt
= 1 – e –(s-a) ∞ / s-a
Q5) Explain System functions for Laplace Transform.
A5)
System functions
The response of an LTI system with impulse response h(t) to complex exponential input x(t) = e st is y(t) = H(s) e st where s ia complex number and
H(s) = 
e -st dt
When s is purely imaginary this is Fourier transform H(jw)
When s is complex this is Laplace transform of h(t) , H(s )
Let z = r e jw and z n = r n e jwn
Then for input z n we get output H(z) z n
Figure 2. I/O relationship
Here H(z) is called the system function.
y[n] =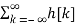 
x[n-k]
= z n 
z-k
Here z transform of h[k] is H[z].
Q6) Find io(t) using Laplace
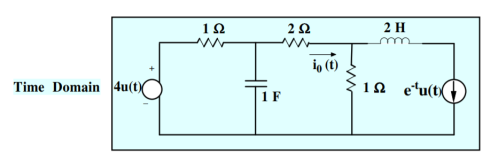
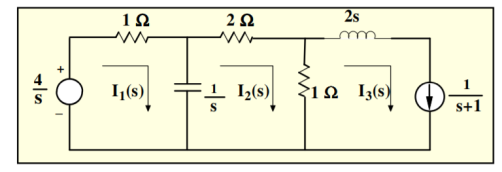
Figure 3. Mesh Network
Figure 4. Laplace network
A6)
Mesh 1:
(s+1)/s I1(s) – I2(s)/s = 4/s
(s+1) I1(s) – I2(s) = 4
Mesh 2:
-1/s I1(s) + 3s+1/s I2(s) – I3(s) =0
-1/s I1(s) + 3s+1/s I2(s) – 1/s+1 =0
-I1(s) + (3s+1) I2(s) = s/s+1
-(s+1) I1(s) + (s+1)(3s+1) I2(s) = s
Adding these two equations we get
S(3s+4) I2(s) = s+4
I2(s) = (1/3) (s+4)/ s(s+4/3) = 1/s -2/3/ s+4/3
i2(t) = [ 1-2/3 e -4/3 t ] u(t)
-I1(s) + 3s+1/s . [1/s -2/3 /s+4/3] =s/s+1
-I1(s) = s/s+1 – 3s+1/s[ 1/s -2/3/s+4/3]
Q7) Using Laplce transform solve the differential equations :
y” – 3y’ -4y = -16x
y(0) = -4
y’(0) = -5
A7)
Apply the operator L to both sides of the differential equation; then use linearity, the initial conditions,
L[ y” – 3y’ -4y] = L[-16x]
L[ y”] – 3L[y’] -4L[y] = L[-16x]
[p 2 L[y] – p y’(0)] –[p L[y] – y[0]] – 4 L[y] = L[-16x]
p 2 L[y] +4p+5]-3[pL[y] +4] -4L[y] = -16/p2
(p2 -3p-4) L[y] + 4p -7 = -16/p2
L[y] = -16/p2 -4p +7/p2 – 3p -4
But the partial fraction decomposition of this expression for L[ y] is
-16/p2 -4p+7/ p2 -3p-4 = -16/p2 -4p+7/ p2 -3p-4 = -16-4p3+7p2/ p2(p+1)(p-4)
= -3/p + 4/p2 +1/p+1 +-2/p-4
Therefore,
y= L-1 [-3/p + 4/p2 + 1/p+1+-2/p-4]
Which yields
y=-3 +4x+e-x -2 e 4x
Q8) Explain Z domain analysis.
A8)
Z domain analysis
Lets look at the system G(z)
G(z) = 1/1-az-1
The system has a pole at z=a and zero at z=0.
The impulse response of the system above is hn= an
Hence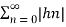 
= 
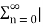a n |= 
n.
For the system to be stable it must have finite sum. As 
a n represents geometric expression te sum is finite if and only if |a|<1.
That means that the POLE must be within the unit circle!
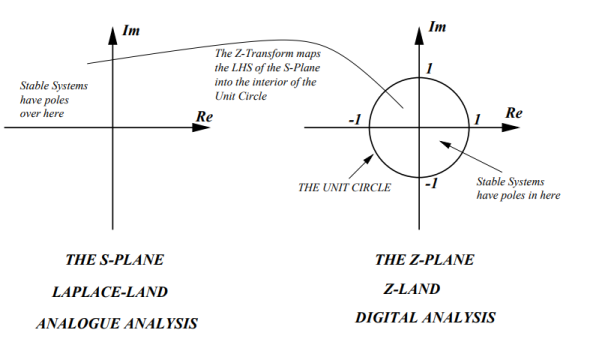
Figure 5. s-plane to z-plane
Q9) Explain poles and zeros of systems and sequences.
A9)
Poles are the values of z that make the denominator zero, and zeros are the values of z that make the numerator go to zero.
G(z) = 1/ 1+0.2 z-1 -0.48 z-2
= z 2/ z2 +0.2 z-0.48
= z2 / (z+0.8) (z-0.6)
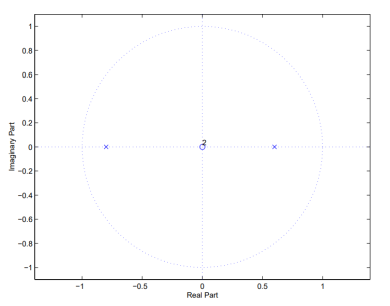
Figure 6. Poles and Zeros
Q10) Explain z-Transform for discrete time signals and systems.
A10)
Given an analog signal x(t) the discrete time signal is represented by a sequence of weighted and delayed impulses.
Figure 7. Discrete time signal
A discrete time system is a mathematucal algorithm that takes an input sequence x[n] and produces output sequence y[n].
For any given sequence x[n] its z-transform is defined as :
X(z) =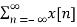 
z -n
= …….+x[-2] z2 + x[-1] z1 + x[0] zo + x[1] z -1 + x[2] z -2 +……..
Where z is complex variable.
Unit - 4
Laplace and z- Transforms
Q1) Find H(z), poles and zeros for the difference equation given by
y[n] – 3/8 y[n-1] – 7/16 y[n-2] = x[n] + x[n-2]
A1)
Here ao=1,a1=-3/8,a2=-7/6,bo=1,b1=0,b2=1
H[z] = 1 + z -2 / 1 -3/8 z-1 -7/16 z -2
= (1+j z-1 ) (1 -jz-1) / (1-7/8 z-1) ( 1+1/2 z-1)
Zeros : z=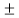
j represented by o.
Poles z= 7/8 , z=-1/2 represented by x.
Figure 1. Poles and Zeros
Q2) Find the Laplace transform of e –t.
A2)
F(s) =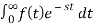 
F(s) = 
F(s) =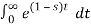 
F(s) = 1 / 1-s [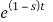
]0 
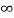
F (s = 1/ s-1.
Q3) Find the Laplace transform of unit -step function.
A3)
f(t) = 1 (t≥0)
F(s) = 
-st dt = -1/s e -st | 0 ∞ = 1/s [ e -∞ - e -0] = 1
F(s) = 1/s.
Q4) Find the Laplace transform of e-at u(t)
A4)
X(s) =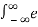 
at u(t) e -st dt = 
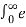at e -st dt = 
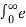–(s-a) t dt
= 1 – e –(s-a) ∞ / s-a
Q5) Explain System functions for Laplace Transform.
A5)
System functions
The response of an LTI system with impulse response h(t) to complex exponential input x(t) = e st is y(t) = H(s) e st where s ia complex number and
H(s) =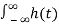 
e -st dt
When s is purely imaginary this is Fourier transform H(jw)
When s is complex this is Laplace transform of h(t) , H(s )
Let z = r e jw and z n = r n e jwn
Then for input z n we get output H(z) z n
Figure 2. I/O relationship
Here H(z) is called the system function.
y[n] =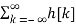 
x[n-k]
= z n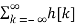 
z-k
Here z transform of h[k] is H[z].
Q6) Find io(t) using Laplace
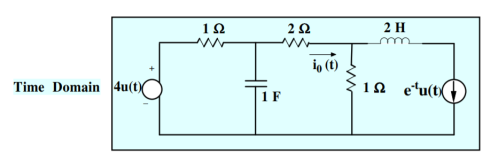
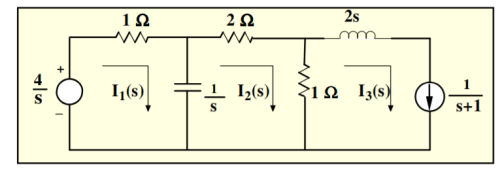
Figure 3. Mesh Network
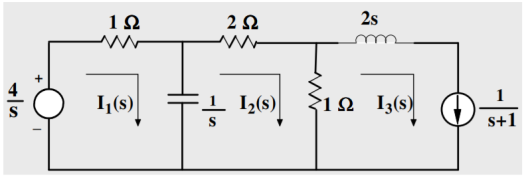
Figure 4. Laplace network
A6)
Mesh 1:
(s+1)/s I1(s) – I2(s)/s = 4/s
(s+1) I1(s) – I2(s) = 4
Mesh 2:
-1/s I1(s) + 3s+1/s I2(s) – I3(s) =0
-1/s I1(s) + 3s+1/s I2(s) – 1/s+1 =0
-I1(s) + (3s+1) I2(s) = s/s+1
-(s+1) I1(s) + (s+1)(3s+1) I2(s) = s
Adding these two equations we get
S(3s+4) I2(s) = s+4
I2(s) = (1/3) (s+4)/ s(s+4/3) = 1/s -2/3/ s+4/3
i2(t) = [ 1-2/3 e -4/3 t ] u(t)
-I1(s) + 3s+1/s . [1/s -2/3 /s+4/3] =s/s+1
-I1(s) = s/s+1 – 3s+1/s[ 1/s -2/3/s+4/3]
Q7) Using Laplce transform solve the differential equations :
y” – 3y’ -4y = -16x
y(0) = -4
y’(0) = -5
A7)
Apply the operator L to both sides of the differential equation; then use linearity, the initial conditions,
L[ y” – 3y’ -4y] = L[-16x]
L[ y”] – 3L[y’] -4L[y] = L[-16x]
[p 2 L[y] – p y’(0)] –[p L[y] – y[0]] – 4 L[y] = L[-16x]
p 2 L[y] +4p+5]-3[pL[y] +4] -4L[y] = -16/p2
(p2 -3p-4) L[y] + 4p -7 = -16/p2
L[y] = -16/p2 -4p +7/p2 – 3p -4
But the partial fraction decomposition of this expression for L[ y] is
-16/p2 -4p+7/ p2 -3p-4 = -16/p2 -4p+7/ p2 -3p-4 = -16-4p3+7p2/ p2(p+1)(p-4)
= -3/p + 4/p2 +1/p+1 +-2/p-4
Therefore,
y= L-1 [-3/p + 4/p2 + 1/p+1+-2/p-4]
Which yields
y=-3 +4x+e-x -2 e 4x
Q8) Explain Z domain analysis.
A8)
Z domain analysis
Lets look at the system G(z)
G(z) = 1/1-az-1
The system has a pole at z=a and zero at z=0.
The impulse response of the system above is hn= an
Hence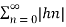 
= 
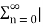a 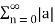n |= 
n.
For the system to be stable it must have finite sum. As 
a n represents geometric expression te sum is finite if and only if |a|<1.
That means that the POLE must be within the unit circle!
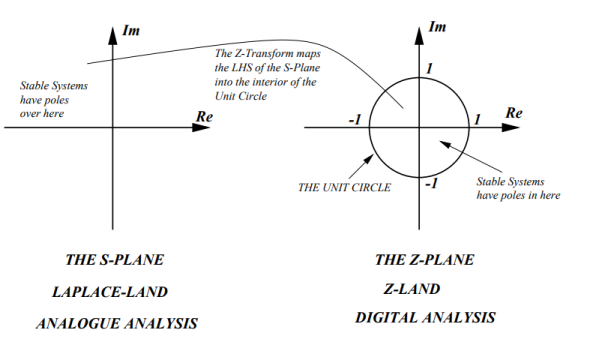
Figure 5. s-plane to z-plane
Q9) Explain poles and zeros of systems and sequences.
A9)
Poles are the values of z that make the denominator zero, and zeros are the values of z that make the numerator go to zero.
G(z) = 1/ 1+0.2 z-1 -0.48 z-2
= z 2/ z2 +0.2 z-0.48
= z2 / (z+0.8) (z-0.6)
Figure 6. Poles and Zeros
Q10) Explain z-Transform for discrete time signals and systems.
A10)
Given an analog signal x(t) the discrete time signal is represented by a sequence of weighted and delayed impulses.
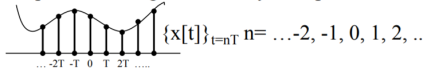
Figure 7. Discrete time signal
A discrete time system is a mathematucal algorithm that takes an input sequence x[n] and produces output sequence y[n].
For any given sequence x[n] its z-transform is defined as :
X(z) = 
z -n
= …….+x[-2] z2 + x[-1] z1 + x[0] zo + x[1] z -1 + x[2] z -2 +……..
Where z is complex variable.
