Unit - 5
Information theory and coding
Q1) A voice grade channel of the telephone network has a bandwidth of 3.4KHz
- Calculate the channel capacity of the telephone channel for a signal to noise ratio of 30db
- Calculate the minimum signalto noise ratio required to support information through the telephone channel at the rate of 4800 bits/sec
A1) Given :
Bandwidth = 3.4 KHz
10 log 10 S/N = 30 db
S/N = 10 3 = 1000
Channel capacity
C = B log 2 (1+S/N) = 3400 log (1 + 1000)
C = 33889 bits/sec
Given C = 4800 bits/sec
4800 = 3400 log 2(1+S?N)
S/N = 2 48/34 - 1
S/N = 1.66
S/N = 10 log 1.66 = 2.2 db
S/N = 2.2 db
Q2) An analog signal has a 4 Khz bandwidth . The signal is sampled at 2.5 times the Nyquist rate and each sample quantized into 256 equally likely levels. Assume that the successive samples are statistically independent.
- Find the information rate of the source
- Can the output of the source be transmitted without error over the Gaussian channel of bandwidth 50Hz and S/N ratio of 20db
- If the output of the source is to be transmitted without errors over an analog channel having S/N of 10 db , Compute bandwidth requirement of the channel.
A2) Given B = 4000Hz Therefore Nyquist rate = 2B = 8000Hz
Sampling rate rs = 2.5 Nyquist rate
= 2.5 x 8000 = 20,000 samples/sec
Since all the quantization levels are equal likely the maximum information content
I = log e q = log 2 256 = 8 bits /sample.
Information rate Rs = rs .I = 20,000 X 8 = 1,60,000 bits/sec
From Shannon’s Hartley law
C = B log (1+ S/N)
C = 332.91 x 10 3 bits/sec
Iii)
C = B log (1+S/N) = Rs
B = Rs/log(1+S/N) = 46.25 KHz
B = 46.25 KHz.
Q3) Determine the capacity of the channel as shown in the figure.
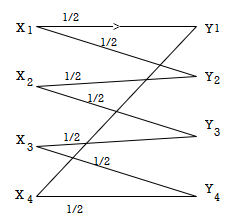
A3) The channel matrix can be written as
P(Y/X) = ½ ½ 0 0 |
0 ½ ½ 0 |
0 0 ½ ½ |
½ 0 0 ½ |
Now h = H(Y/X) = 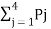 log 1/Pj
log 1/Pj
H = ½ log 2 + ½ log 2 +0+ 0 = 1 bits/Msg symbol.
Channelcapacity
C = log s – h
= log 4 – 1
= 1 bits/msg symbol.
Q4) For the channel matrix shown find the channel capacity
P(bj/ai) = 
A4) The given matrix belongs to a symmetric or uniform channel
H(B/A) = h = 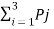 log 1/Pj
log 1/Pj
= ½ log 2 + 1/3 Log 3 + 1/6 log 6
H(B/A) = 1.4591 bits/msg symbol.
The channel capacity is given by
C = (log S – h) rs rs = 1 msgsymbol/sec
C = log 3 – 1.4591
C = 0.1258 bits/sec
Q5) Construct a Shannon-fano ternary code for the following ensenble and find the code efficiency and redundancy.Also draw the corresponding code tree.
S = { S1,S2,S3,S4,S5,S6,S7}
P={ 0.3,0.3,0.12,0.12,0.06,0.06,0.04} with
X= {0,1,2}
A5)
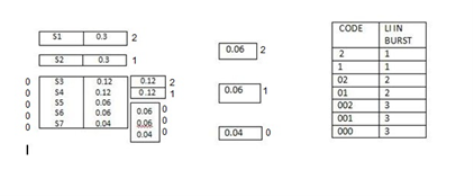
The average length of the ternary tree is given by
L = 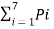 li -----------------(1)
li -----------------(1)
= 0.3 x 1 + 0.3 x 1 + 0.12 x 2 +0.12 x 2 + 0.06 x3 +0.06x 3 +0.04 x 3
L = 1.56 trinits/msg symbol.
Entropy in bits/msg symbolis given by
H(s) = 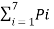 log 1/Pi
log 1/Pi
= 0.3 log 1/0.3 x 2 + 0.12 log1/0.12 x2 + 0.06 log 1/0.06 x 2 +0.04 log 1/0.04
= 2.4491 bits/msg symbol.
Now entropy in r-ary units per message symbol is given by
H r (s) = H(s) / log 2 r
r=3
H3 (s) = H(s) / log 2 3 = 2.4419/ log 2 3 = 1.5452.
The terenary coding effeciency is given by
ηc = H3(s) / L = 1.5452/ 1.56 = 0.99 bits/msg symbol.
ηc = 99.05%
Q6) You are given four messages X1 , X2 , X3 and X4 with respective probabilities 0.1,0.2,0.3,0.4
- Device a code with pre-fix property (Shannon fano code) for these messages and draw the code.
- Calculate the efficiency and redundancy of the code.
- Calculate the probabilities of 0’s and 1’s in the code.
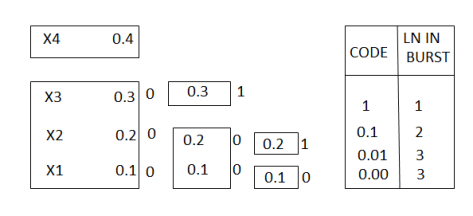
A6) Average length L =  li
li
= 0.4 x1 + 0.3 x 2 + 0.2 x 3 + 0.1 x3
L = 1.9 bits/symbol.
Entropy H(s) = 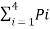 log 1/Pi
log 1/Pi
= 0.4 log 1/0.4 + 0.3 log 1/0.3 + 0.2 log 1/0.2 + 0.1 log 1/0.1
H(s) = 1.846 bits/msg symbol.
Code efficiency ηc = H(s) / L = 1.846/1.9 = 97.15%
Code Redundancy = R ηc = 1- ηc = 2.85%
The code tree can be drawn
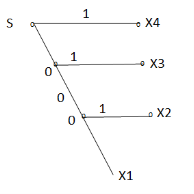
The probabilities of 0’s and 1’s in the code are found by using the
P(0)= 1/L 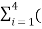 no of 0’s in code xi) (Pi)
no of 0’s in code xi) (Pi)
= 1/1.9 [ 3 x 0.1 + 2x 0.2 + 1x 0.3 + 0(0.4)]
P(0) = 0.5623
P(1) = 1/L  no of 1’s in code xi) (Pi)
no of 1’s in code xi) (Pi)
= 1/1.9 [ 0x0.1+1x0.2+1x0.+1x0.4]
P(1) = 0.4737
Q7) Given are the messages X1,X2,X3,X4,X5,X6 with respective probabilities 0.4,0.2,0.2,0.1,0.07 and 0.03. Construct a binary code by applying Shannon-fano encoding procedure . Determine code effeciency and redundancy of the code.
A7) Applying Shannon-fano encoding procedure

Average length L is given by
L = 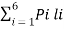
= 0.4 x 1 + 0.2 x 3 + 0.2 x 3 + 0.1 x 3 + 0.07 x4 + 0.03 X 4
L = 2.3 bits/msg symbol.
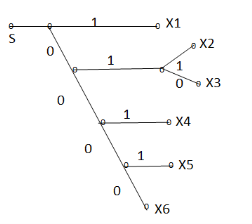
Entropy
H(s) = 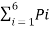 log 1/Pi
log 1/Pi
0.4 log 1/0.4 + 2x 0.2 log 1/0.2 + 0.1 log 1/0.1 + 0.07 log 1/0.07 + 0.03 log 1/0.03
H(s) = 2.209 bits/msg symbol.
Code Efficiency = ηc = H(s) / L = 2.209/2.03 = 96.04%
Code Redundancy = R ηc = 1- ηc = 3.96%
Q8) Given the messages X1,X2,X3,X4,X5 and X6 with respective probabilities of 0.4,0.2,0.2,0.1,0.07 and 0.03. Construct a binary code by applying Huffman encoding procedure . Determine the efficiency and redundancy of the code formed.

A8) Now Huffmann code is listed below:
Source Symbols | Pi | Code | Length (li) |
X1 | 0.4 | 1 | 1 |
X2 | 0.2 | 01 | 2 |
X3 | 0.2 | 000 | 3 |
X4 | 0.1 | 0010 | 4 |
X5 | 0.07 | 00110 | 5 |
X6 | 0.03 | 00111 | 5 |
Now Average length (L) = 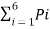 li
li
L = 0.4 x 1 + 0.2 x 2 + 0.2 x 3 + 0.1 x 4 + 0.07x 5 + 0.03 x 5
L = 2.3 bits/msg symbol.
Entropy H(s) = = 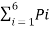 log 1/Pi
log 1/Pi
0.4 log 1/0.4 + 0.2 log 1/0.2 + 0.1 log 1/0.1 + 0.07 log 1/0.07 + 0.03 log 1/0.03
H(s) = 2.209 bits /msg symbol.
Code effeciency = nc = H(s) /L = 2.209/2.3 = 96.04%.
Q9) Apply Shannon’s encoding (binary algorithm) to the following set of messages and obtain code efficiency and redundancy.
m 1 | m 2 | m 3 | m 4 | m 5 |
1/8 | 1/16 | 3/16 | ¼ | 3/8 |
A9)
Step 1:
The symbols are arranged according to non-incraesing probabilities as below:
m 5 | m 4 | m 3 | m 2 | m 1 |
3/8 | ¼ | 3/16 | 1/16 | 1/8 |
P 1 | P 2 | P 3 | P 4 | P 5 |
The following sequences of 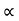 are computed
are computed
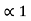 = 0
= 0
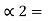 P1 +
P1 + 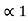 = 3/8 + 0 = 0.375
= 3/8 + 0 = 0.375
 = P2 +
= P2 + 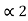 = ¼ + 0.375 = 0.625
= ¼ + 0.375 = 0.625
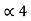 = P3 +
= P3 + 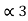 = 3/16 + 0.625 = 0.8125
= 3/16 + 0.625 = 0.8125
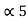 = P4 +
= P4 + 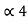 = 1/16 + 0.8125 = 0.9375
= 1/16 + 0.8125 = 0.9375
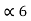 = P5 +
= P5 +  = 1/8 + 0.9375 = 1
= 1/8 + 0.9375 = 1
Step 3:
The smallest integer value of li is found by using
2 li ≥ 1/Pi
For i=1
2 l1 ≥ 1/P1
2 l1 ≥ 1/3/8 = 8/3 = 2.66
The samllest value ofl1 which satisfies the above inequality is 2 therefore l1 = 2.
For i=2 2 l2 ≥ 1/P2 Therefore 2 l2 ≥ 1/P2
2 l2 ≥ 4 therefore l2 = 2
For i =3 2 l3 ≥ 1/P3 Therefore 2 l3 ≥ 1/P3 2 l3 ≥ 1/ 3/16 = 16/3 l3 =3
For i=4 2 l4 ≥ 1/P4 Therefore 2 l4 ≥ 1/P4
2 l4 ≥ 8 Therefore l4 = 3
For i=5
2 l5 ≥ 1/P5 Therefore
2 l5 ≥ 16 Therefore l5=4
Step 4
The decimal numbers 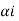 are expanded in binary form upto li places as given below.
are expanded in binary form upto li places as given below.
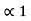 = 0
= 0
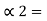 0.375
0.375
0.375 x2 = 0.750 with carry 0
0.75 x 2 = 0.50 with carry 1
0.50 x 2 = 0.0 with carry 1
Therefore
(0.375) 10 = (0.11)2
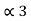 = 0.625
= 0.625
0.625 X 2 = 0.25 with carry 1
0.25 X 2 = 0.5 with carry 0
0.5 x 2 = 0.0 with carry 1
(0.625) 10 = (0.101)2
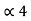 = 0.8125
= 0.8125
0.8125 x 2 = 0.625 with carry 1
0.625 x 2 = 0.25 with carry 1
0.25 x 2 = 0. 5 with carry 0
0.5 x 2 = 0.0 with carry 1
(0.8125) 10 = (0.1101)2
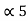 = 0.9375
= 0.9375
0.9375 x 2 = 0.875 with carry 1
0.875 x 2 = 0.75 with carry 1
0.75 x 2 = 0.5 with carry 1
0.5 x 2 = 0.0 with carry 1
(0.9375) 10 = (0.1111)2
 = 1
= 1
Step 5:
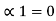 and l1 = 2 code for S1 ----00
and l1 = 2 code for S1 ----00
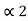 =(0.011) 2 and l2 =2 code for S2 ---- 01
=(0.011) 2 and l2 =2 code for S2 ---- 01
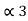 = (.101)2 and l3 =3 code for S3 ------- 101
= (.101)2 and l3 =3 code for S3 ------- 101
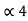 = (.1101)2 and l4 =3 code for S ----- 110
= (.1101)2 and l4 =3 code for S ----- 110
 = (0.1111)2 and l5 = 4 code for s5 --- 1111
= (0.1111)2 and l5 = 4 code for s5 --- 1111
The average length is computed by using
L = 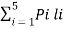
= 3/8 x 2 + ¼ x 2 + 3/16 x 3 + 1/8 x 3 + 1/16 x 4
L= 2.4375 bits/msg symbol
The entropy is given by
H(s) = 3/8 log (8/3) + ¼ log 4 + 3/16 log 16/3 + 1/8 log 8 + 1/16 log 16
H(s) =2.1085 bits/msg symbol.
Code efficiency is given by
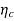 = H(s)/L = 2.1085/2.4375 = 0.865
= H(s)/L = 2.1085/2.4375 = 0.865
Percentage code effeciency = 86.5%
Code redundancy
R 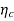 = 1 -
= 1 - 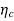 = 0.135 or 13.5%.
= 0.135 or 13.5%.
Q10) A discreter message source S emits two independent symbols X and Y with probabilities 0.55 and 0.45 respectively. Calculate the effeciency of the source and its redundancy.
A10) Given H(s) = 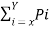 log 1/Pi
log 1/Pi
Px log 1/Px + Py log 1/Py
= 0.55 log 1/0.55 + 0.45 log 1/0.45
= 0.9928 bits/msg symbol.
The maximum entropy is given by
H(s) max = log 2 q = log 2 2 = 1 bits/symbol.
The source effeciency is given by
 = H(s) max/ H(s) = 0.9928/1 = 0.9928
= H(s) max/ H(s) = 0.9928/1 = 0.9928
 = 99.28 %
= 99.28 %
The source redundacy is given by
Rs = 1- 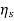 = 0.0072
= 0.0072
Rns = 0.72%
Q11) Verify that the rule of additivity for the following source S= {S1,S2,S3,S4} with P={1/2,1/3,1/12,1/12}
A11) The entropy H(s) is given by
H(s) = 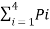 log 1/Pi
log 1/Pi
= ½ log 2 2 + 1/3 log 2 3 + 2 x 1/12 log 2 12
H(s) = 1.6258 bits/msg symbol.
From additive property we have
H’(s) = P1 log (1/P1) + (1-P1) log 1/(1-P1)
= (1-P1){ P2/(1-P1) log (1-P1)/P2 + P3/(1-P1) log(1-P1)/P3 + P4/(1-P1) log (1-P1)/P4
= 1/2 log 2 + ½ Log 2 + ½ { (1/3)/(1/2) log(1/2)/(1/2) + (1/12)/1/2 log(1/12)/(1/2) + (1/12)/(1/2) log (1/2) /(1/12)
H’(s) = 1.6258 bits/symbol.
Q12) Find the entopy of the source in bits/symbol of the source that emits one out of four symbols A,B,C and D in a statistically independent sequences with probabilities ½,1/4,1/8 and 1/8 .
A12) The entropy of the source is given by
H(s) =  log 1/Pi
log 1/Pi
= Pa log 1/Pa + Pb log 1/Pb + Pc log 1/Pc + Pd log 1/Pd
= ½ log 2 2 + ¼ log 2 4 + 1/8 log 2 8 + 1/8 log 2 8
H(s) = 1.75 bits/msg symbol.
1 nat = 1.443 bits
1bit = 1/1.443 = 0.693 nats.
Entropy of the souce H(s) = 1.75 X 0.693 =
H(s) = 1.213 nats/symbol.
Q13) Let X represent the outcome of a single roll of a fair die. What is the entropy of X?
A13) Since a die has six faces , Probability of getting any number is 1/6.
Px = 1/6.
So entropy of X = H(X) = Px log 1/Px = 1/6 log 6 = 0.431 bits / msg symbol.
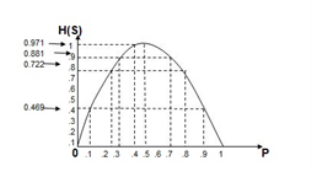
Q14) A binary source is emitting an independent sequence of 0s and 1s with probabilities p and 1-p respectively. Plot entopy of source versus p.
A14) The entropy of the binary source is given by
H(s) = 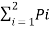 log 1/Pi
log 1/Pi
= P1 log 1/P1 + P2 log 1/P2
= P log (1/P) + (1-P) log 1/(1- P)
P=0.1 = 0.1 log(1/0.1) + 0.9 log(1/0.9)
= 0.469 bits/symbol.
At p=0.2
0.2 log(1/0.2) + 0.8 log(1/0.8)
= 0.722 bits/symbol.
At p=0.3
0.3 log(0.3) + 0.7 log(1/0.7)
= 0.881 bits/symbol.
At p=0.4
0.4 log(0.4) + 0.6 log(1/0.6)
= 0.971 bits/symbol.
At p=0.5
0.5 log(0.5) + 0.5 log(1/0.5)
= 1 bits/symbol.
At p=0.6
H(s) = 0.6 log (1/0.6) + 0.4 log(1/0.4)
H(s) = 0.971 biys/symbol
At p=0.7
0.7 log(1/0.7) + 0.3 log(1/0.3)
= 0.881 bits/symbol.
At p=0.8
0.8 log (1/0.8) +0.2 log(1/0.2)
0.722 bits/symbol
At p=0.9
0.9 log(1/0.9) + 0.1 log(1/0.1)
=0.469 bits /symbol.
Q15) The collector volatge of a certain circuit lie between -5V and -12V.The voltage can take only these values -5,-6,-7,-9,-11,-12 volts with the respective probabilities 1/6,1/3,1/12,1/12,1/6,1/6. This voltage is recorded with a pen recorder. Determine the average self information associated with the record in terms of bits/level.
A15) Given Q = 6 levels. P= {1/6,1/3,1/12,1/12,1/6,1/6}
Average self-information H(s) = 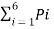 log 2 1/Pi
log 2 1/Pi
= 1/6 log 26 + 1/3 Log 23 + 1/12 log 2 12 + 1/12 log 2 12 + 1/6 Log 26 + 1/6 Log 26
H(s) = 2.418 bits/level
Q16) Consider a source S={S1,S2,S3} with P={1/2,1/4,1/4} Find
a) Self information
b) Entropy of source S
A16)
a) Self information of S1 = I1 = log 21/P1 = Log 2 2 = 1 bit
Self information of S2 = I2 = log 2 1/P2 = Log 2 4 = 2 bits
Self information of S3 = I3 = log 2 1/P3 = Log 2 4 = 2 bits
b) Average Information content or Entropy =
H(s) = 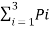 Ii
Ii
= I1 P1 + I2 P2 + I3 P3
= ½(1) + ¼(2) + ¼ (2)
= 1.5 bits/msg symbol.
Q17) Let us consider a binary source with source alphabet S={S1,S2} with probabilities P= {1/256, 255/256}
A17) Entorpy H(s) = 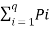 log 1/Pi
log 1/Pi
= 1/256 log 256 + 255/256 log 256/255
H(s) = 0.037 bits / msg symbol.
Q18) Let S = {S3,S4} with P’ = {7/16,9/16}. Determine entropy.
A18) Then Entropy H(s’) = 7/16 log 16/7 + 9/16 log 16/9
H(s) = 0.989 bits/msg symbol.
Q19) Explain basic information system?
A19) Information system can be defined as the message that is generated from the information source and transmitted towards the receiver through transmission medium.
The block diagram of an information system can be drawn as shown in the figure.

Information sources can be classified into
- Analog Information Source
- Digital Information Source
Analog Information source such as microphone actuated by speech or a TV camera scanning a scene, emit one or more continuous amplitude electrical signals with respect to time.
Discrete Information source such as teletype or numerical output of computer consists of a sequence of discrete symbols or letters.
An analog information source can be transformed into discrete information source through the process of sampling and quantizing.
Discrete Information source are characterized by
- Source Alphabet
- Symbol rate
- Source alphabet probabilities
- Probabilistic dependence of symbol in a sequence.
In the block diagram of the Information system as shown in the figure, let us assume that the information source is a discrete source emitting discrete message symbols S1, S2………………. Sq with probabilities of occurrence given by P1, P2…………. Pq respectively. The sum of all these probabilities must be equal to 1.
Therefore P1+ P2 + ………………. + Pq = 1----------------------(1)
Or 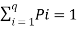 --------------------(2)
--------------------(2)
Symbols from the source alphabet S = {s1, s2……………….sn} occurring at the rate of “rs” symbols/sec.
The source encoder converts the symbol sequence into a binary sequence of 0’s and 1s by assigning code-words to the symbols in the input sequence.
Transmitter
The transmitter couples the input message signal to the channel. Signal processing operations are performed by the transmitter include amplification, filtering and modulation.
Channel
A communication channel provides the electrical connection between the source and the destination.The cahnnel may be a pair of wires or a telephone cable or a free space over the information bearing symbol is radiated.
When the binary symbols are transmitted over the channel the effect of noise is to convert some of the 0’s into 1’s and some of the 1’s into 0’s. The signals are then said to be corrupted by noise.
Decoder and Receiver
The source decoder converts binary output of the channel decoder into a symbol sequence. Therefore the function of the decoder is to convert the corrupted sequence into a symbol sequence and the function of the receiver is to identify the symbol sequence and match it with the correct sequence.
Q20) Given the messages X1,X2,X3,X4,X5 and X6 with respective probabilities of 0.4,0.2,0.2,0.1,0.07 and 0.03. Construct a binary code by applying Huffman encoding procedure . Determine the efficiency and redundancy of the code formed.
A20)
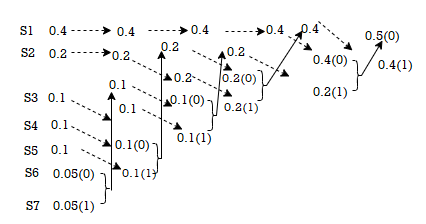
Now Huffmann code is listed below:
Source Symbols | Pi | Code | Length (li) |
X1 | 0.4 | 1 | 1 |
X2 | 0.2 | 01 | 2 |
X3 | 0.2 | 000 | 3 |
X4 | 0.1 | 0010 | 4 |
X5 | 0.07 | 00110 | 5 |
X6 | 0.03 | 00111 | 5 |
Now Average length (L) = 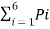 li
li
L = 0.4 x 1 + 0.2 x 2 + 0.2 x 3 + 0.1 x 4 + 0.07x 5 + 0.03 x 5
L = 2.3 bits/msg symbol.
Entropy H(s) = = 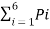 log 1/Pi
log 1/Pi
0.4 log 1/0.4 + 0.2 log 1/0.2 + 0.1 log 1/0.1 + 0.07 log 1/0.07 + 0.03 log 1/0.03
H(s) = 2.209 bits /msg symbol.
Code effeciency = nc = H(s) /L = 2.209/2.3 = 96.04%.
Q21) The generator matrix for a block code is given below. Find all code vectors of this code

A21) The Generator matrix G is generally represented as
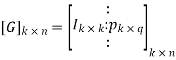
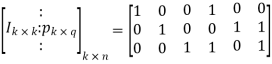
On comparing,
The number of message bits, k = 3
The number of code word bits, n = 6
The number of check bits, q = n – k = 6 – 3 = 3
Hence, the code is a (6, 3) systematic linear block code. From the generator matrix, we have Identity matrix

The coefficient or submatrix,
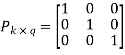
Therefore, the check bits vector is given by,
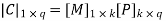
On substituting the matrix form,
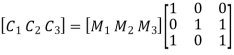
From the matrix multiplication, we have
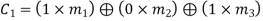


On simplifying, we obtain
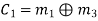

Hence the check bits (c1 c2 c3) for each block of (m1 m2 m3) message bits can be determined.
(i) For the message block of (m1 m2 m3) = (0 0 0), we have
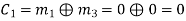


(ii) For the message block of (m1 m2 m3) = (0 0 1), we have
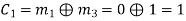
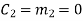
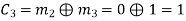
(iii) For the message block of (m1 m2 m3) = (0 1 0), we have


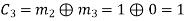
Similarly, we can obtain check bits for other message blocks.
Q22) The generator polynomial of a (7, 4) cyclic code is G(p) = p3 + p + 1. Find all the code vectors for the code in non-systematic form
A22)
Here n = 7, k = 4
Therefore, q = n – k = 7 – 4 = 3
Since k = 4, there will be a total of 2k = 24 = 16 message vectors (From 0 0 0 0 to 1 1 1 1). Each can be coded in to a 7 bits codeword.
(i) Consider any message vector as
M = (m3 m2 m1 m0) = (1 0 0 1)
The general message polynomial is M(p) = m3p3 + m2p2 + m1p + m0, for k = 4
For the message vector (1 0 0 1), the polynomial is
M(p) = 1. p3 + 0. p2 + 0. p + 1
M(p) = P3 + 1
The given generator polynomial is G(p) = p3 + p + 1
In non-systematic form, the codeword polynomial is X (p) = M (p). G (p)
On substituting,
X (p) = (p3 + 1). (p3 + p +1)
= p6 + p4 + p3 + p3 + p +1
= p6 + p4 + (1 1) p3 + p +1
= p6 + p4 + p + 1
= 1.p6 + 0.p5 + 1.p4 + 0.p3 + 0.p2 + 1.p + 1
The code vector corresponding to this polynomial is
X = (x6 x5 x4 x3 x2 x1 x0)
X = (1 0 1 0 0 1 1)
(ii) Consider another message vector as
M = (m3 m2 m1 m0) = (0 1 1 0)
The polynomial is M(p) = 0.p3 + 1.p2 + 1.p1 + 0.1
M(p) = p2 + p
The codeword polynomial is
X(p) = M(p). G(p)
X(p) = (p2 + p). (p3 + p + 1)
= p5 + p3 + p2 + p4 + p2 + p
= p5 + p4 + p3 + (1 1) p2 + p
= p5 + p4 + p3 + p
= 0.p6 + 1.p5 + 1.p4 + 1.p3 + 0.p2 + 1.p + 0.1
The code vector, X = (0 1 1 1 0 1 0)
Similarly, we can find code vector for other message vectors also, using the same procedure.
Q23) The generator polynomial of a (7, 4) cyclic code is G(p) = p3 + p + 1. Find all the code vectors for the code in systematic form.
A23)
Here n = 7, k = 4
Therefore, q = n - k = 7 – 4 = 3
Since k = 4, there will be a total of 2k = 24 = 16 message vectors (From 0 0 0 0 to 1 1 1 1). Each can be coded into a 7 bits codeword.
(i) Consider any message vector as
M = (m3 m2 m1 m0) = (1 1 1 0)
By message polynomial,
M(p) = m3p3 + m2p2 + m1p + m0, for k = 4.
For the message vector (1 1 1 0), the polynomial is
M(p) = 1.p3 + 1.p2 + 1.p + 0.1
M(p) = p3 + p2 + p
The given generator polynomial is G(p) = p3 + p + 1
The check bits vector polynomial is
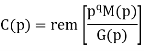
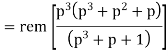
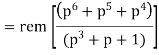
We perform division as per the following method.
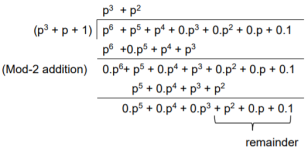
Thus, the remainder polynomial is p2 + 0.p + 0.1.
This is the check bits polynomial C(p)
c(p) = p2 + 0.p + 0.1
The check bits are c = (1 0 0)
Hence the code vector for the message vector (1 1 1 0) in systematic form is
X = (m3 m2 m1 m0⋮ c2 c1 c0) = (1 1 1 0 1 0 0)
(ii) Consider another message vector as
M = (m3 m2 m1 m0) = (1 0 1 0)
The message polynomial is M(p) = p3 + p
Then the check bits vector polynomial is
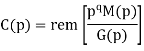

The division is performed as below.
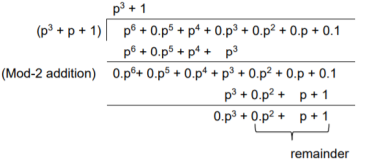
Thus, the check bits polynomial is C(p) = 0.p2 + 1.p + 1.1
The check bits are C = (0 1 1)
Hence the code vector is X= (1 0 1 0 0 1 1)
Similarly, we can find code vector for other message vectors also, using the same procedure.
Q24) Generate the CRC code for the data word of 1 1 1 0. The divisor polynomial is p3 + p + 1
A24)
Data Word (Message bits) = 1 1 1 0
Generator Polynomial (divisor) = p3 + p + 1
Divisor in binary form = 1 0 1 1
The divisor will be of (q + 1) bits long. Here the divisor is of 4 bits long. Hence q = 3. We append three 0s to the data word.
Now the data sequence is 1 1 1 0 0 0 0. We divide this data by the divisor of 1 0 1 1. Binary division is followed.
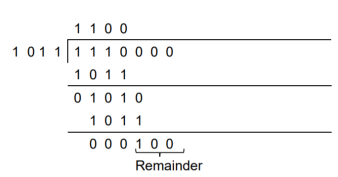
The remainder obtained from division is 100. Then the transmitted codeword is 1 1 1 0 1 0 0.
Q25) A codeword is received as 1 1 1 0 1 0 0. The generator (divisor) polynomial is p3 + p + 1. Check whether there is error in the received codeword.
A25)
Received Codeword = 1 1 1 0 1 0 0
Divisor in binary form = 1 0 1 1
We divide the received codeword by the divisor.

The remainder obtained from division is zero. Hence there is no error in the received codeword.