Unit - 1

Fluids and Their Properties

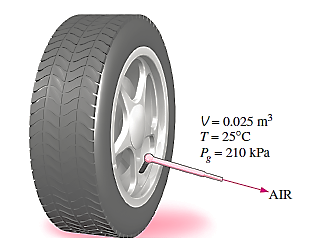
Q1) The temperature of the air in an automobile tyre affects the pressure in the tyre. The pressure gauge reads 210 kPa when the air temperature is 25°C. Determine the pressure rise in the Tyre when the air temperature in the Tyre rises to 50°C if the volume of the Tyre is 0.025 m3. Calculate how much air must be bled out to return pressure to its former value at this temperature. Assume a pressure of 100 kPa in the atmosphere.

A1)

Assumptions:

1 At specified conditions, air behaves as an ideal gas.

2 The volume of the tire remains constant.

Properties:

Analysis:

Initially the absolute pressure in the tyre is

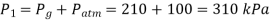
Treating air as an ideal gas and assuming the volume of the tire to remain

Constant, the final pressure in the tire is determined from

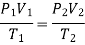
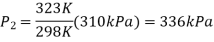
Thus, the pressure rise is

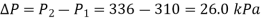
The amount of air that needs to be bled off to restore pressure to its original value is,

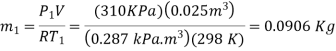
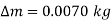
Q2) What is cavitation? What causes it?

A2)

In the flow of a liquid, cavitation is the vaporization that may occur at locations where the pressure drops below the vapor pressure. The vapor bubbles collapse as they are swept away from the low-pressure regions,

Generating highly destructive, extremely high-pressure waves. This phenomenon is a common cause for drop in performance and even the erosion of impeller blades.

Q3) The water temperature in a plumbing system is kept below 40°C. To avoid cavitation, determine the lowest pressure that can be allowed in the system. The vapor pressure of water at 40°C is 7.38 kPa.

A3)

The vapor pressure of water at 40°C is 7.38 kPa.

To avoid cavitation, the pressure anywhere in the flow should not be allowed to drop below the vapor (or saturation) pressure at the given temperature. That is,

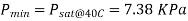
Therefore, the pressure should be maintained above 7.38 kPa everywhere in flow.

Q4) When an ideal gas is compressed isothermally from 10 atm to 11 atm, the density of the gas reduces by 10%. If a gas is compressed isothermally from 100 atm to 101 atm, calculate the percent drop in density.

A4)

The Gas behaves as ideal gas,

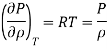
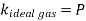
Therefore, the coefficient of compressibility of an ideal gas is equal to its absolute pressure, and the coefficient of compressibility of the gas increases with increasing pressure.

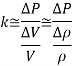
Therefore, the percent increase of density of an ideal gas during isothermal compression is equal to the percent increase in pressure.

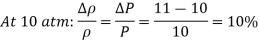
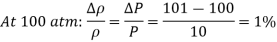
Therefore, a pressure changes of 1 atm causes a density change of 10% at 10 atm and a density change of 1% at 100 atm.

Q5) Isothermally, water at 1 atm pressure is compressed to 800 atm pressure. Calculate the increase in water density. Assume that water has an isothermal compressibility of .

A5)

1 The isothermal compressibility is constant in the given pressure range.

2 An approximate analysis is performed by replacing differential changes by finite changes

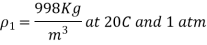
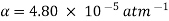
When differential quantities are replaced by differences and the properties α and β are assumed to be constant, the change in density in terms of the changes in pressure and temperature is expressed approximately as,

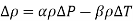
The change in density due to a change of pressure from 1 atm to 800 atm at constant temperature is

Q6) At constant pressure, water at 15°C and 1 atm pressure is heated to 100°C. Determine the change in water density using coefficient of volume expansion data.

A6)

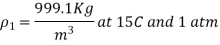
The coefficient of volume expansion at the average temperature of (15+95)/2 = 55°C is,

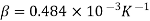
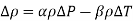
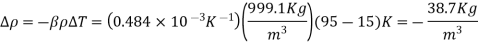
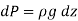Q7) The density of seawater at a free surface where the pressure is 98 kPa is approximately 1030 kg/m3. Taking the bulk modulus of elasticity of seawater to be and expressing variation of pressure with depth z as determine the density and pressure at a depth of 2500 m. Disregard the effect of temperature

A7)

Q8) What is viscosity? What is the cause of it in liquids and in gases? Do liquids or gases have higher dynamic viscosities?

A8)

Viscosity is a measure of the “stickiness” or “resistance to deformation” of a fluid. It is due to the internal frictional force that develops between different layers of fluids as they are forced to move relative to each other.

Viscosity is caused by the cohesive forces between the molecules in liquids, and by the molecular collisions in gases. In general, liquids have higher dynamic viscosities than gases.

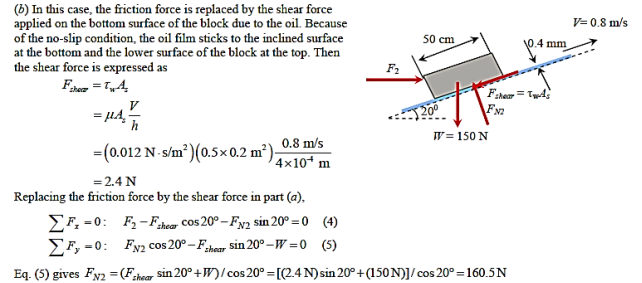
Q9) A 50-cm " 30-cm " 20-cm block weighing 150 N is to be moved at a constant velocity of 0.8 m/s on an inclined surface with a friction coefficient of 0.27. (a) Determine the force F that needs to be applied in the horizontal direction. (b) If a 0.4-mm-thick oil film with a dynamic viscosity of 0.012 Pa.s is applied between the block and inclined surface, determine the percent reduction in the required force

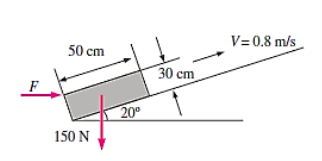
A9)

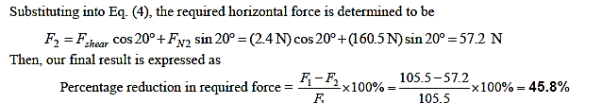
Q10) The dynamic viscosity of oil is 0.027 Pa.s., and a thin 20cm x 20cm flat plate is pushed horizontally at 1 m/s through a 3.6-mm-thick oil layer sandwiched between two plates, one stationary and the other moving at a constant velocity of 0.3 m/s, as indicated. Assuming that the velocity in each oil layer varies linearly, (a) plot the velocity profile to locate the point where the oil velocity is zero, and (b) calculate the force required to maintain this motion on the plate.

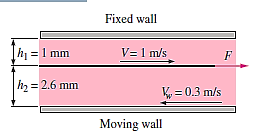
A10)

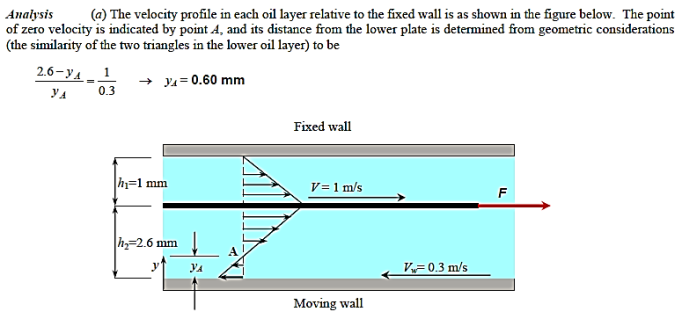
Q11) At 68°F, a 0.03-inch glass tube is put into kerosene. Kerosene has a 26-degree contact angle with glass. Calculate the kerosene's capillary increase in the tube.

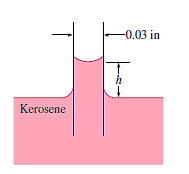
A11)

The surface tension of kerosene-glass at 68F (20C)

The density of kerosene-glass at 68F (20C)

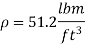
The contact angle of kerosene with the glass surface is given to be 26°.

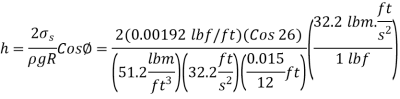
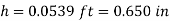
Q12) When a 1.9-mm-diameter tube is placed into an unknown liquid with a density of 960 kg/m3, the liquid rises 5 mm in the tube, forming a 15-degree contact angle. Calculate the liquid's surface tension.

A12)

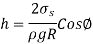
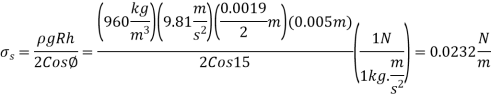
Q13) Determine the gage pressure inside a soap bubble of diameter (a) 0.2 cm and (b) 5 cm at 20°C.

A13)

The soap bubble is in atmospheric air.

The surface tension of soap water at 20C is,

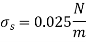
The pressure difference between the inside and the outside bubble is given by

In open atmosphere,

So,

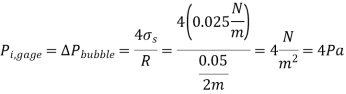
Q14) Because of the capillary effect, nutrients dissolved in water are transferred to the upper regions of plants through small tubes. Determine how high the water solution in a 0.005-mm-diameter tube will rise in a tree due to the capillary effect. At 20°C, with a contact angle of 15°, treat the solution as water.

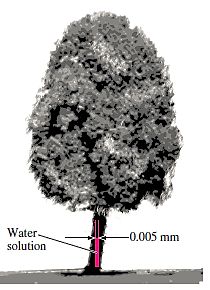
A14)

Assumptions

1 The solution can be treated as water with a contact angle of 15°.

2 The diameter of the tube is constant. 3 The temperature of the water solution is 20°C.

The surface tension of water at 20°C is

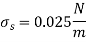
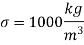
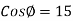
So,

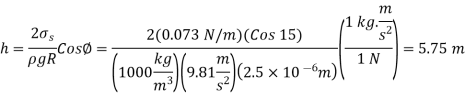
Q15) Explain Hypothesis of continuum.

A15)

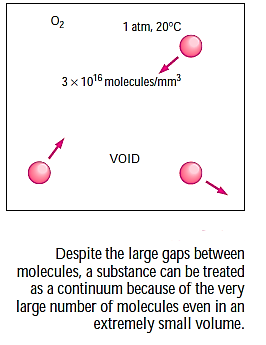
In the gas phase, matter is made up of atoms that are widely dispersed. However, it is highly easy to dismiss a substance's atomic nature and see it as a continuous, homogenous mass with no holes, i.e. a continuum. Using the continuum idealisation, we may consider qualities as point functions and assume that they fluctuate continuously in space with no jump discontinuities.

This idealisation holds true as long as the size of the system in question is big in comparison to the space between the molecules.

Except for a few specific issues, this is true for almost all problems. Many of our claims, such as "the density of water in a glass is the same at every position," are implicit in the continuum idealisation.

Consider a container filled with oxygen under atmospheric conditions to get a feel of the distances involved at the molecular level.

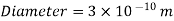
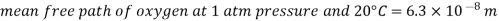
That is, an oxygen molecule travels, on average, a distance of 6.3×10^(-8)  m (about 200 times its diameter) before it collides with another molecule.

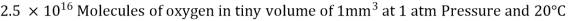
The continuum model is valid as long as the system's characteristic length (such as its diameter) is significantly greater than the mean free path of the molecules. The mean free path can grow quite enormous at very high vacuums or very high heights (for example, atmospheric air at 100 km elevation has a mean free path of around 0.1 m). In such instances, the rarefied gas flow theory should be applied, with the influence of individual molecules considered.

Q16) Derive the formula for shear stress in a moving fluid.

A16)

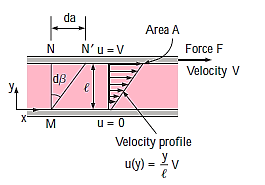
Consider a fluid layer separated by a distance between two extremely big parallel plates (or, equivalently, two parallel plates submerged in a vast body of a fluid). The top plate is now subjected to a constant parallel force F while the bottom plate remains stationary.

Following the first transients, the top plate travels continually under the influence of this force at a constant velocity V. The fluid in contact with the top plate adheres to the plate surface and flows at the same velocity as it, and the shear stress 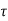acting on this fluid layer is

Consider the movement of a fluid across a plate's surface. The fluid layer in contact with the surface will use friction to draw the plate along, putting a friction force on it. Similarly, due of the friction between the two layers, a quicker fluid layer will try to drag the neighbouring slower layer and impose a friction force. Shear stress is defined as friction force per unit area and is denoted by .

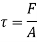
Where A denotes the area of contact between the plate and the fluid. It is worth noting that the fluid layer deforms continually as a result of shear stress.

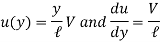
Where y is the vertical distance from the lower plate.

During a differential time, interval dt, the sides of fluid particles along a

Vertical line MN rotate through a differential angle while the upper plate

Moves a differential distance 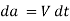. The angular displacement or deformation (or shear strain) can be expressed as,

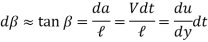
Rearranging, the rate of deformation under the influence of shear stress

Becomes

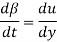
As a result, we infer that a fluid element's rate of deformation is identical to the velocity gradient du/dy. Furthermore, it can be demonstrated experimentally that the rate of deformation (and consequently the velocity gradient) is exactly proportional to the shear stress in most fluids.

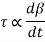
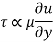
Newtonian fluids are fluids in which the rate of deformation is proportional to the shear stress. Newtonian fluids include most ordinary fluids such as water, air, gasoline, and oils. Non-Newtonian fluids include blood and liquid polymers. Shear stress may be described linearly in one-dimensional shear flow of Newtonian fluids.

For most fluids, shear stress is proportional to velocity gradient, and shear stress at the wall surface is as where the constant of proportionality is termed the fluid's dynamic viscosity.

The fluids that that obey the linear relationship above are called Newtonian fluids,

In fluid flow and heat transfer studies, the ratio of dynamic viscosity to density appears frequently. For convenience, this ratio is given the name kinematic viscosity,

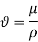
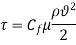
Where Cf is the dimensionless friction coefficient.

The shear force operating on a Newtonian fluid layer (or, according to Newton's third law, the force acting on the plate) is defined as

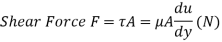
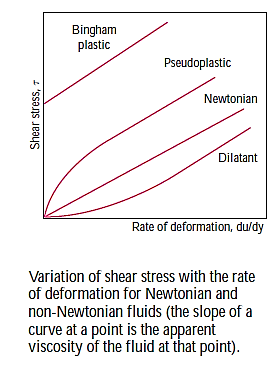
Q17) Classify Fluids based on Shear force.

A17)

Newtonian Fluid (Fluid Mechanics)

• The Newtonian fluid is the fluid in which the shear stress is directly proportional to the rate of shear strain or velocity gradient.

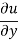
• All gases are Newtonian fluids. E.g.: Glycerine, kerosene. Air, water, alcohol etc.
• The linear relationship between shear stress and the rate of deformation is called as Newtonian fluid.
   

Non-Newtonian Fluid (Rheology)

• The fluid in which the shear stress is not directly proportional to the rate of shear strain or Velocity gradient, is called as Non-Newtonian Fluid.
• e.g., Slurries, toothpaste, gels, polymer solution paint, lubricant oils.

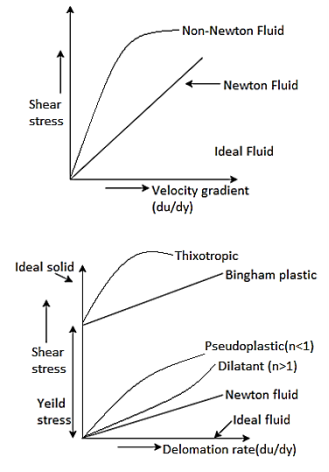
• The non-linear relationship between shear stress and the rate of deformation is called as non-Newtonian fluid.
   

Pseudo plastic Fluid or Shear Thinning Fluid:

• Fluid in which the apparent viscosity decreases with increasing deformation rate (n< 1) is called as Pseudoplastic fluid.
• Examples are slurries, mud, polymer solution, quicksand, gums, blood, milk, colloidal suspensions paper pulp in water, ketchup.

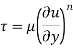
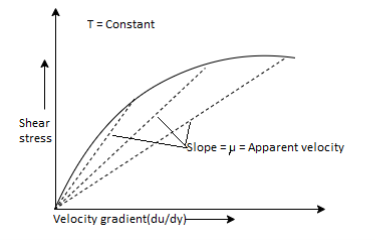
Dilatant Fluid or Shear Thickening fluid:

• Fluid in which the apparent viscosity increases with increasing deformation rate (n>1) is called as dilatant fluids.
• e.g., Suspension of sand, starch, butter, sugar solution.

Bingham Plastic Fluid

• The fluid which possesses a definite yield stress but then the relationship between shear stress and angular deformation is linear is called as Bingham plastic fluid.
   
• e.g., Sewage sludge, toothpaste, oil paint, jellies, applesauce, drilling mud.

Thixotropic Fluid or Plastic Fluid:

• The fluid which possesses a definite yield stress but then the relationship between shear stress and angular deformation is nonlinear are called as Thixotropic fluid. e.g., Printer ink, lipstick.
   

Ideal Fluid:

The fluid which has zero viscosity er shear stress is always zero is called as ideal fluid, that's why ideal fluid is represented by the horizontal axis.

Q18) Explain the phenomenon of Surface tension.

A18)

A drop of blood forms a hump on a horizontal glass; a drop of mercury forms a near-perfect sphere and can be rolled over a smooth surface just like a steel ball; water droplets from rain or dew hang from branches or leaves of trees; liquid fuel injected into an engine forms a mist of spherical droplets; water dripping from a leaky faucet falls as spherical droplets; a soap bubble released into the air forms.

In these and other observations, liquid droplets behave like little spherical balloons filled with the liquid, and the liquid's surface behaves like a stretched elastic membrane under stress. The attraction interactions between the liquid molecules generate the pulling force that causes this tension to act parallel to the surface. Surface tension is the magnitude of this force per unit length.

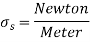
Consider two liquid molecules, one on the surface and the other deep into the liquid body. Because of symmetry, the attractive forces exerted on the inside molecule by the surrounding molecules balance each other. However, the attractive forces exerted on the surface molecule are not symmetric, and the attractive forces provided by the gas molecules above are often negligible. As a result, there is a net attractive force acting on the molecule at the liquid's surface, which tends to drag the molecules on the surface into the liquid's centre.

This force is countered by the repulsive forces generated by the compressed molecules under the surface.

As a result of the compression effect, the liquid's surface area is reduced. This explains why liquid droplets prefer to take on a spherical form, which has the least surface area for a given volume.

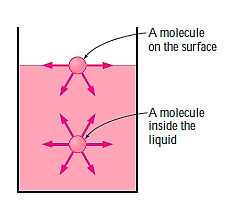
Consider a liquid film (such as the film of a soap bubble) hung on a U-shaped wire frame with a moveable side to better comprehend the surface tension effect. Normally, the liquid film draws the moveable wire inward to reduce its surface area. To counteract this pulling action, a force F must be supplied to the moveable wire in the opposite direction. Because the thin film in the device has two sides accessible to air (the top and bottom surfaces), the length along which the tension operates in this situation is 2b.

Then a force balance on the movable wire gives

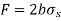
Thus, surface Tension,

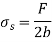
The force F stays constant in the U-shaped wire while the moveable wire is pushed to stretch the film and increase its surface area.

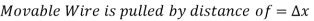
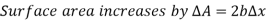
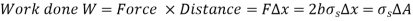
Because the force is constant in this scenario. This finding may alternatively be understood as the film's surface energy increasing by during the stretching process, which is consistent with the alternate interpretation of as surface energy. As a result, surface tension may alternatively be defined as the work done per unit increase in the liquid's surface area.

The surface tension of a material changes substantially depending on its composition and temperature. Mercury droplets produce spherical balls that can be rolled on a surface like a solid ball without soaking it.

In general, the surface tension of a liquid falls with temperature until it reaches zero at the critical point (thus, there is no distinguishable liquid–vapor barrier at temperatures above the critical point). Pressure has a minor influence on surface tension.

Impurities can significantly alter a substance's surface tension. As a result, some compounds known as surfactants can be added to a liquid to reduce its surface tension. Soaps and detergents, for example, reduce the surface tension of water and allow it to permeate through the microscopic gaps between fibres for more efficient cleaning. However, because of poor craftsmanship, equipment whose performance is dependent on surface tension (such as heat pipes) might be ruined by the presence of contaminants.

Only at liquid–liquid or liquid–gas interfaces do we talk about surface tension for liquids. As a result, while defining surface tension, it is critical to include the neighbouring liquid or gas. Surface tension also influences the size of the liquid droplets that form. A droplet that continues to develop by adding additional mass will collapse when the surface tension can no longer hold it together. This is analogous to a balloon that will explode during inflation if the pressure within exceeds the strength of the balloon material.

A curved interface denotes a pressure differential (or "pressure jump") across the interface, with pressure greater on the concave side. Consider the free-body diagram of half a droplet or bubble to estimate the surplus pressure inside a droplet or bubble above atmospheric pressure. Given that surface tension works around the circumference and pressure acts on the area, horizontal force balances for the droplet and bubble result in

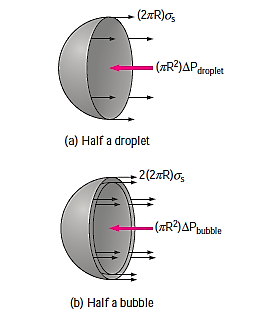
Where denotes the pressures inside and outside the droplet or bubble. is just atmospheric pressure while the droplet or bubble is in the atmosphere. The bubble has a factor 2 in the force balance because it is made up of a film with two surfaces (inner and outer surfaces) and hence two circumferences in the cross section.

Excess pressure in a droplet (or bubble) may also be calculated by taking into account a differential increase in the radius of the droplet owing to the addition of a differential quantity of mass and interpreting the surface tension as an increase in surface energy per unit area. The rise in the surface energy of the droplet as a result of this differential expansion process is thus

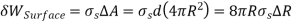
The expansion work performed during this differential process is calculated by multiplying the force by the distance.

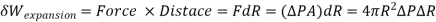
Equating the two expressions above gives

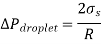
Q19) Derive the equation for rise or fall of a liquid in a tube.

A19)

Microscopically, the capillary effect may be explained by considering cohesive forces (the forces between similar molecules, such as water and water) and adhesive forces (the forces between unlike molecules, such as water and glass). At the solid–liquid interface, liquid molecules are susceptible to both cohesive forces from other liquid molecules and adhesive forces from solid molecules. The magnitudes of these forces govern whether or not a liquid wet a solid surface.

Water molecules are obviously more strongly attracted to glass molecules than to other water molecules, and hence water tends to climb along the glass surface.

The converse is true for mercury, which suppresses the liquid surface towards the glass wall.

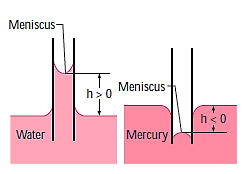
A force balance on the cylindrical liquid column of height h in the tube can be used to calculate the amount of the capillary rise in a circular tube. Because the bottom of the liquid column is at the same level as the reservoir's free surface, the pressure there must be atmospheric. As a result, the air pressure acting at the top surface is balanced, and the two effects cancel each other out.

The weight of the liquid column is approximately

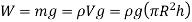
Equating the vertical component of the surface tension force to the weight gives

Solving for h gives the capillary rise to be,

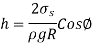
This relationship applies to nonwetting liquids (such as mercury in glass) and yields the capillary drop. In this example, and therefore , resulting in a negative h. As a result, a negative capillary rise value equates to a capillary drop

Q20) Explain about Cavitation.

A20)

Water at 10°C, for example, will flash into vapour and create bubbles if the pressure drops below 1.23 kPa (such as the tip regions of impellers or the suction sides of pumps). The vapour bubbles (dubbed cavitation bubbles because they generate "cavities" in the liquid) burst when they are carried away from low-pressure areas, causing very destructive, extremely high-pressure waves.

This condition is a typical cause of decreased performance and

Cavitation refers to the erosion of impeller blades and is a significant concern in the design of hydraulic turbines and pumps.

Cavitation should be avoided (or at least minimised) in flow systems because it decreases performance, creates irritating vibrations and noise, and damages equipment. Pressure spikes caused by a high number of bubbles bursting near a solid surface over time may cause erosion, surface pitting, fatigue failure, and eventually the destruction of the components or machinery. Cavitation in a flow system can be detected by its characteristic tumbling sound.