Unit - 2

Pressures and Head

Q1) The air pressure in a tank is measured with a manometer. The fluid has a specific gravity of 1.25, and the manometer's differential height between the two arms is 28 inches. Determine the absolute pressure in the tank for the cases of the manometer arm with the (a) higher and (b) lower fluid level linked to the tank if the local atmospheric pressure is 12.7 psia.

A1)

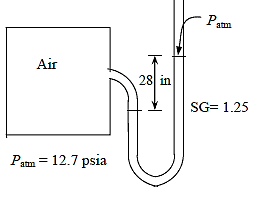
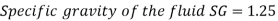
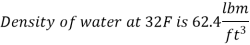
The density of the fluid is obtained by multiplying its specific gravity by the density of water,

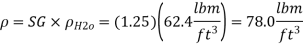
The pressure difference corresponding to a differential height of 28 in between the two arms of the manometer is

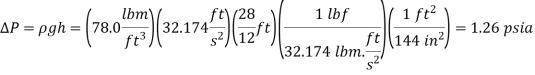
Then the absolute pressures in the tank for the two cases become,

The fluid level in the arm attached to the tank is higher (vacuum):

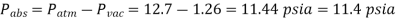
The fluid level in the arm attached to the tank is lower:

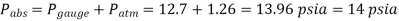
Q2) What is Pascals law?

A2)

The compressive force per unit area is known as pressure, and it appears to be a vector. Pressure in a fluid, on the other hand, is constant in all directions. It is a scalar quantity since it contains magnitude but not a definite direction. Consider a small wedge-shaped fluid element of unit length (into the page) in equilibrium, as illustrated in the diagram.

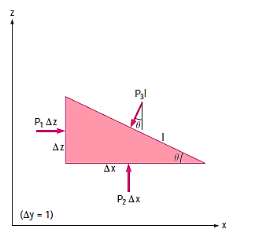
The mean pressures at the three surfaces are

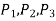
The force acting on a surface is the product of mean pressure and the surface area.

From Newtons 2nd Law a force balance,

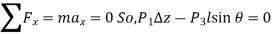
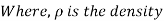
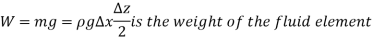
The wedge is a right triangle,

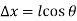
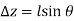
Substituting these geometric relations and dividing by

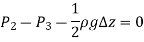
As, and the fluid element decreases to a point when the wedge gets minuscule. The findings of these two relations are then combined to yield

Regardless of the angle

A similar conclusion can be obtained by repeating the analysis for an element in the xz-plane. As a result, we can deduce that the pressure at a given place in a fluid is the same in all directions. It can be demonstrated that this result holds true for fluids in motion as well as fluids at rest in the absence of shear forces.

Q3) What do you mean by the term hydrostatic paradox?

A3)

The hydrostatic paradox

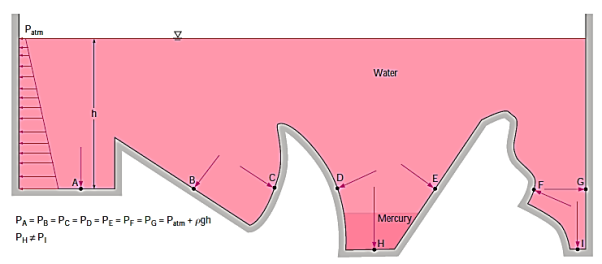
Because they are at the same depth and are connected by the same static fluid, the pressures at points A, B, C, D, E, F, and G are the same.

However, although being at the same depth, the pressures at locations H and I are not the same since these two points cannot be interconnected by the same fluid (i.e., we cannot construct a curve from point I to point H while always remaining in the same fluid). (Can you figure out where the pressure is higher?) Furthermore, the fluid's pressure force is always normal to the surface at the indicated places.

Because the pressure in a fluid remains constant in the horizontal direction, applying pressure to a confined fluid increases the pressure by the same amount throughout. This is known as Pascal's law. Pascal also understood that a fluid's force is related to its surface area. He understood that by connecting two hydraulic cylinders of various sizes, the larger might be used to exert a proportionally greater force than the smaller. Many technologies that are part of our daily lives, such as hydraulic brakes and lifts, can be traced back to "Pascal's machine."

Q4) Explain bourdon tube.

A4)

The Bourdon tube, named after the French engineer and inventor Eugene Bourdon (1808–1884), is a mechanical pressure measurement device that consists of a hollow metal tube bent like a hook whose end is closed and attached to a dial indicator needle. The tube is undeflected when it is open to the atmosphere, and the needle on the display is calibrated to read zero at this point (gage pressure). The tube stretches and moves the needle in accordance with the pressure applied when the fluid inside the tube is pressured.

Despite their widespread use, manometers are not well suited to detecting extremely high pressures or pressures that change rapidly over time. They also necessitate the measuring of one or more column heights, which, while not difficult, can be time-consuming. Other types of pressure-measuring tools have been developed to address some of these issues. The majority of these are based on the premise that when a pressure is applied to an elastic structure, the structure will deform, and the size of the deformation may be connected to the pressure. The Bourdon pressure gauge is probably the most well-known example of this type of gadget.

The hollow, elastic curved tube Bourdon tube, which is coupled to the pressure source as indicated, is the most important mechanical element in this gauge. The tube straightens as the pressure inside it rises, and although though the deformation is slight, it may be translated into the motion of a pointer on a dial, as shown. The indicated pressure is gauge pressure because it is the difference in pressure between the outside of the tube atmospheric pressure and the inside of the tube that causes the tube to move.

The Bourdon gauge must be calibrated so that the dial reading accurately indicates the pressure in psi, psf, or pascals. When the gauge reads zero, it means the recorded pressure is the same as the local atmospheric pressure. A negative gauge pressure( vacuum) as well as positive pressures can be measured with this type of gauge.

Another form of mechanical gauge for detecting atmospheric pressure is the aneroid barometer. The traditional Bourdon gauge is not adequate for this measurement because atmospheric pressure is reported as an absolute pressure. The common aneroid barometer is made up of a hollow, closed, elastic element that has been evacuated to near absolute zero pressure. The element deflects as the external atmospheric pressure varies, and this motion can be translated into the movement of an attached dial. The dial, like the Bourdon gauge, can be calibrated to give direct atmospheric pressure readings in millimetres or inches of mercury.

Q5) Explain the working of Manometer & derive its equations for general case.

A5)

As,

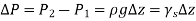
Above equation suggests that a fluid column can be used to measure pressure differences.

A manometer is a gadget that works on this concept and is widely used to monitor minor and moderate pressure variations. A manometer is essentially a glass or plastic U-tube filled with one or more fluids, such as mercury, water, alcohol, or oil. If substantial pressure variations are expected, heavier fluids such as mercury are utilised to keep the size of the manometer to a bearable level.

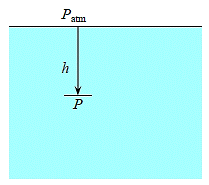
Consider the manometer in the image, which is used to gauge the tank's pressure. The pressure in the tank and at position 1 is the same since the gravitational effects of gases are insignificant. Furthermore, because pressure in a fluid does not vary horizontally, the pressure at point 2 is the same as the pressure at point 1.

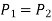
The static equilibrium differential fluid column of height h is open to the atmosphere. The pressure at point 2 is then calculated using Equation.

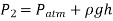
Where is the fluid density in the tube. It's worth noting that the tube's cross-sectional area has no bearing on the differential height h, and consequently the fluid's pressure.

However, the tube's diameter should be large enough (at least a few millimetres) to eliminate the surface tension effect and hence the capillary rise.

Multiple immiscible fluids of varying densities piled on top of each other are used in many engineering issues including some manometers. It's easy to study such systems if you recall that

• The pressure change over a fluid column of height h is

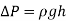
• Pressure increases downward in each fluid and decreases upward

• Two points at the same elevation in a continuous fluid at rest are at the same pressure.

The last concept, which is based on Pascal's law, permits us to "jump" from one fluid column to the next in manometers without worrying about pressure changes as long as we don't jump over another fluid and the fluid remains at rest. The pressure at any place can thus be calculated by starting with a known pressure point and then adding or removing 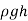terms as we go closer to the point of interest.

Starting at the free surface, where the pressure is , we can ascertain the pressure at the bottom of the tank by descending downward until we reach point 1 at the bottom and setting the result equal to P1.

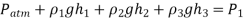
Due to the presence of a device such as a valve or heat exchanger, or any barrier to flow, manometers are particularly well-suited to measuring pressure drops over a horizontal flow section between two specified sites. This is accomplished by connecting the manometer's two legs to these two locations, as indicated.

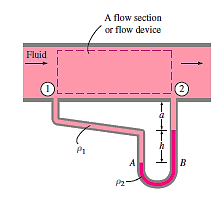
The working fluid can be either a gas or a liquid,

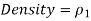
The density of the manometer fluid

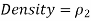
The differential fluid height is h

A relation for the pressure difference can be obtained by starting at point 1 with 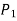, moving along the tube by adding or subtracting the terms until we reach point 2, and setting the result equal to .

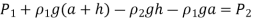
Because the pressure at both sites is the same, we leaped from point A to point B horizontally and ignored the region underneath. Simplifying,

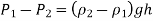
The distance a has no bearing on the outcome, but it must be considered in the analysis. In addition, if the fluid going through the pipe is a gas, then

The relation simplifies to,

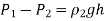
Q6) Explain Strain-gage pressure transducers.

A6)

The Bourdon tube cannot adapt to quick changes in pressure due to its comparatively large mass.

To circumvent this problem, a different form of transducer is utilised, one with a thin, elastic diaphragm in contact with the fluid as the sensing element. The diaphragm deflects as pressure changes, and this deflection can be measured and translated into an electrical voltage. Strain gauges can be placed on the surface of the diaphragm that is not in contact with the fluid or on an element attached to the diaphragm to accomplish this. These gauges can accurately detect small diaphragm strains and provide a voltage output proportional to pressure.

This sort of transducer can accurately measure both static and dynamic pressures, as well as small and big pressures.

A diaphragm deflects between two chambers that are open to pressure inputs. The strain gauge expands as the diaphragm stretches in response to a change in pressure differential across it, and a Wheatstone bridge circuit amplifies the output. A capacitance transducer operates in a similar way, but instead of measuring resistance change as the diaphragm extends, it measures capacitance change.

Q7) Explain Piezoelectric transducers.

A7)

Although strain-gage transducers can be built to have a good frequency response 1up to about 10 kHz2, they become less sensitive at higher frequencies because the diaphragm must be stiffened to produce the greater frequency response. As an alternative, a piezoelectric crystal can be employed as both the elastic element and the sensor in the diaphragm.

Solid-state pressure transducers work on the idea that when a crystalline substance is subjected to mechanical pressure, an electric potential is created in it. The piezoelectric (or press-electric) effect is a phenomenon first identified by brothers Pierre and Jacques Curie in 1880. Piezoelectric pressure transducers offer a far faster frequency response than diaphragm units, making them ideal for high-pressure applications. However, they are not as sensitive as diaphragm-type transducers.

The distortion of the crystal causes a voltage to arise when pressure is applied to it. The applied pressure is directly proportional to the voltage. This sort of transducer can be used to measure both extremely low and very high pressures (up to about 100,000 psi) at high frequencies, depending on the design.

Q8) Air pressurises the water in a tank, and the pressure is measured with a multifluid manometer, as depicted. Determine the air pressure in the tank's gauge.

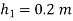
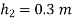
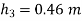
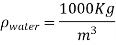
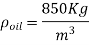
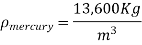
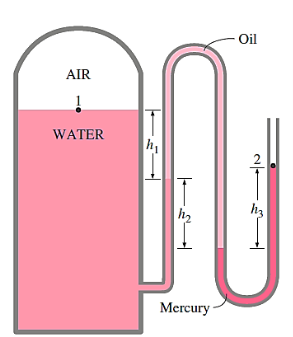
A8)

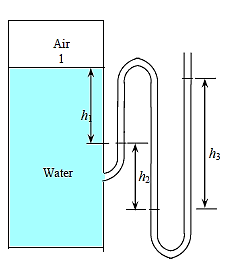
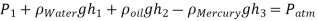
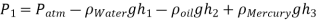
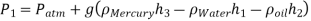
As,

So,

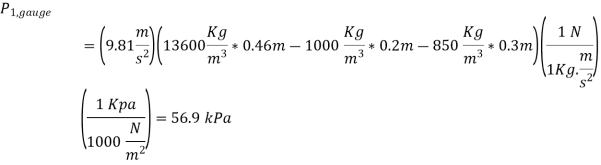
Q9) Determine the atmospheric pressure at a location where the barometric reading is 750 mmHg. Take the density of mercury to be 13,600 kg/m3.

A9)

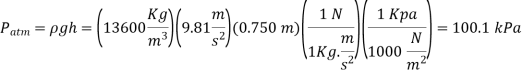
Q10) At a depth of 3 m, the gauge pressure in a liquid is 28 kPa. Determine the gauge pressure at a depth of 12 m in the same liquid.

A10)

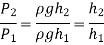
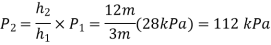
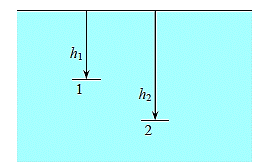
Q11) At a depth of 5 metres, the absolute pressure in the water is 145 kPa. Calculate (a) the local atmospheric pressure and (b) the absolute pressure in a liquid with a specific gravity of 0.85 at the same location at a depth of 5 m.

A11)

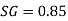
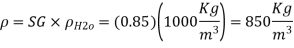
Knowing the absolute pressure, the atmospheric pressure will be,

The absolute pressure at a depth of 5 m in the other liquid is,

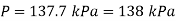
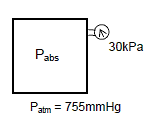
Q12) At a place where the barometric measurement is 755 mmHg, a vacuum gauge linked to a tank reads 30 kPa. Determine the tank's absolute pressure. Assume a density of Hg=13,590 kg/m3.

A12)

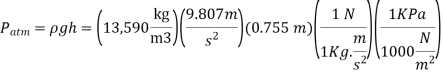
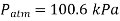
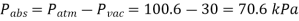
Q13) A mountain hiker's barometer reads 930 mbars at the start of a climb and 780 mbars at the finish. Determine the vertical distance climbed while disregarding the effect of height on local gravitational acceleration. Assume a density of 1.20 kg/m3 for the air.

A13)

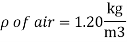
Taking an air column between the top and the bottom of the mountain and writing a force balance per unit base area, we obtain

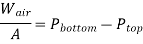
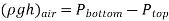
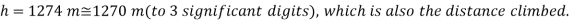
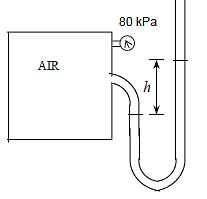
Q14) A gas tank's pressure is measured using both a gauge and a manometer. Determine the distance between the two fluid levels of the manometer if the pressure gauge measurement is 80 kPa.

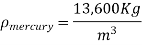
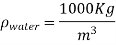
A14)

The gage pressure is related to the vertical distance h between the two fluid levels by

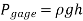
For mercury:

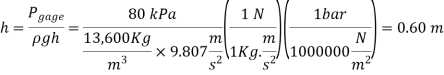
For water:

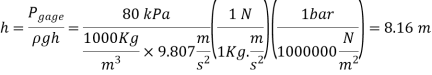
Q15) A tank filled with air is connected to a manometer carrying oil (density=850 kg/m3). Determine the absolute pressure of the air in the tank if the oil level differential between the two columns is 45 cm and the atmospheric pressure is 98 kPa.

A15)

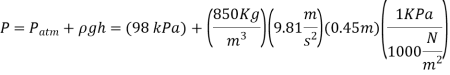
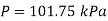
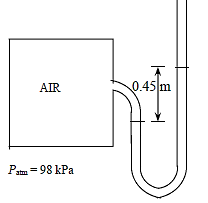
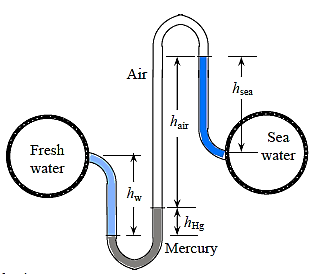
Q16) A twin U-tube manometer is used to connect freshwater and seawater moving in parallel horizontal pipelines, as depicted. Calculate the difference in pressure between the two pipelines. Assume a density of 1035 kg/m3 for seawater at that location. Is it possible to omit the air column in the analysis?

A16)

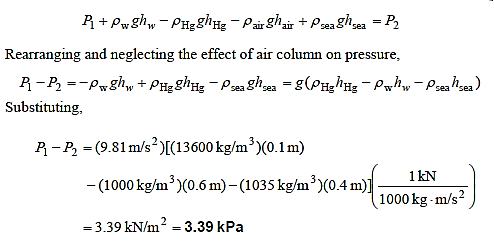
Q17) The manometer is used to measure the pressure in a natural gas pipeline with one of the arms open to the atmosphere, where the local atmospheric pressure is 14.2 psia. Determine the pipeline's absolute pressure.

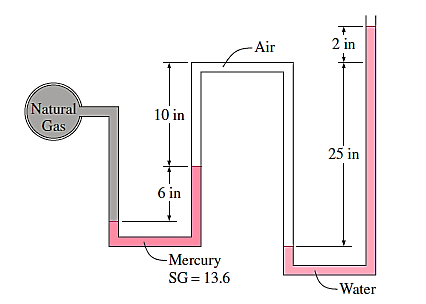
A17)

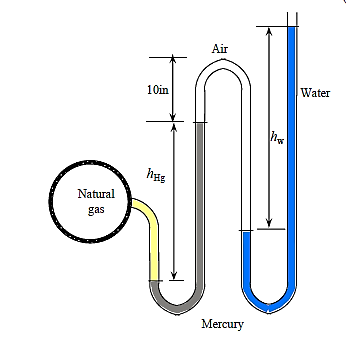
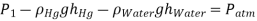
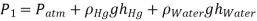
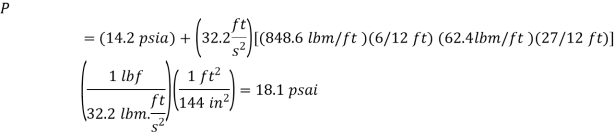
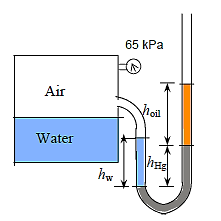
Q18) The air pressure in the tank has been recorded at 65 kPa. Calculate the mercury column's difference height h.

A18)

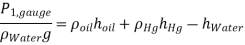
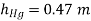
Q19) Calculate the atmospheric pressure at a place with a barometric pressure of 740 mm Hg and a gravitational acceleration of 9.81 m/s2. Assume that mercury is at a temperature of 10°C and has a density of 13,570 kg/m3.

A19)

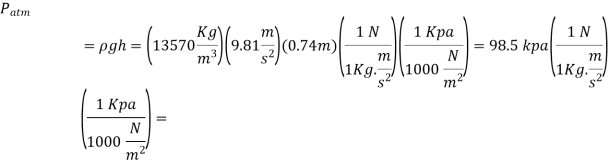
Q20) As indicated, the piston of a vertical piston–cylinder system holding a gas weighs 60 kg and has a cross-sectional area of 0.04 m2. The gravitational acceleration is 9.81 m/s2 and the local air pressure is 0.97 bar. (a) Determine the cylinder's internal pressure. (a) Do you think the pressure inside the cylinder will change if some heat is given to the gas and its volume is doubled?

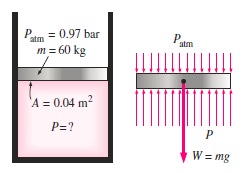
A20)

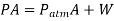
Because the volume change has no influence on the free-body diagram, the pressure inside the cylinder remains constant.

Discussion When the volume of a gas is twice under constant pressure, the absolute temperature doubles if it acts like an ideal gas.