Unit - 3

Static Forces on Surface and Buoyancy

Q1) What do you mean by pressure prism.

A1)

The force created by a fluid operating on a planar rectangular region can be represented graphically in a way that is both informative and practical. Consider the pressure distribution along a vertical wall of a tank with a fixed width b and a given specific weight of liquid.

Since the pressure must vary linearly with depth we can represent the variation as

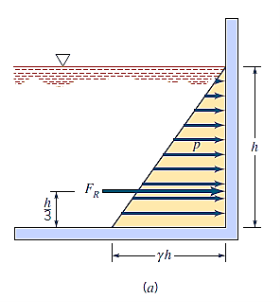
Where the pressure is equal to zero at the upper surface and equal to at the bottom.

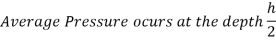
The resultant force acting on the rectangular area,

The three-dimensional representation of the pressure distribution can be drawn as follows

The flat surface of interest is the base of this "volume" in pressure-area space, and its altitude at each point is the pressure. The pressure prism is the volume of the resultant force operating on the rectangular surface, and it is obvious that the magnitude of the resultant force acting on the rectangle surface is equal to the volume of the pressure prism.

The Fluid force is,

The resulting force must pass through the pressure prism's centroid. The centroid of the volume under examination is placed along the surface's vertical axis of symmetry and at a distance above the base (since the centroid of a triangle is located at   above its base).

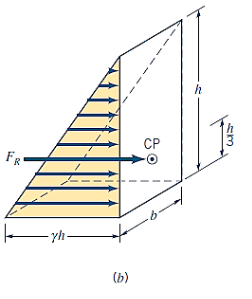
Same graphical approach can be used for plane rectangular surfaces that do not extend up to the fluid surface,

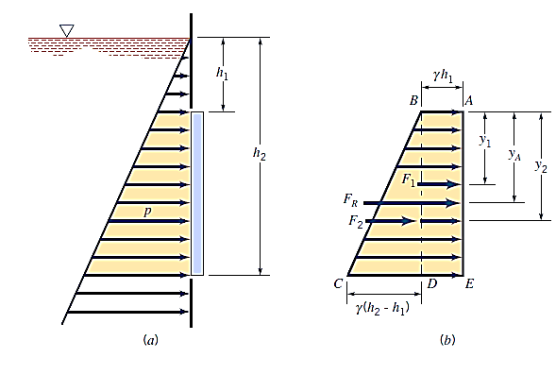
The pressure prism's cross section is trapezoidal in this case. The resultant force, however, is still equal in magnitude to the pressure prism's volume, and it flows via the volume's centroid. Decomposing the pressure prism into two pieces, ABDE and BCD, as indicated, yields certain values.

The components can be easily identified by looking for rectangular surfaces. Summing moments along a convenient axis, such as one passing through A, can be used to find the location of . In this situation,

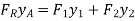
The pressure prism can still be formed for inclined plane rectangular surfaces, and the cross section of the prism will be trapezoidal in most cases.

Q2) Explain the concept of forces on curved plate.

A2)

The computation of the resultant hydrostatic force for a submerged curved surface is more complicated because it often includes the integration of pressure forces that change direction along the curved surface. Because of the intricate shapes involved, the pressure prism notion isn't much use in this scenario.

The horizontal and vertical components 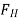and 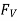 must be determined individually to obtain the resultant hydrostatic force acting on a two-dimensional curved surface. The free body diagram of the liquid block surrounded by the curved surface and the two plane surfaces (one horizontal and one vertical) going through the two ends of the curved surface are used to accomplish this.

The horizontal surface of the liquid block is simply the projection of the curved surface on a horizontal plane, and the vertical surface is simply the projection of the curved surface on a vertical plane.

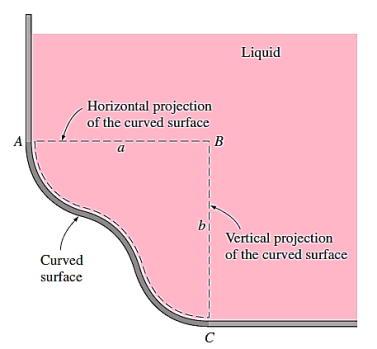
Newton's third law states that the force acting on the curved solid surface is equal to and opposite to the force acting on the curved liquid surface.

It is possible to determine the force operating on the imaginary horizontal or vertical plane surface, as well as its path of action.

The weight of the enclosed liquid block of volume is,

It acts downward through the centroid of this volume. Noting that the fluid block is in static equilibrium, the force balances in the horizontal and vertical directions give,

• The horizontal component of the hydrostatic force acting on a curved surface is equal to the hydrostatic force acting on the curved surface's vertical projection (in magnitude and line of action).
• The vertical component of the hydrostatic force acting on a curved surface equals the hydrostatic force acting on the curved surface's horizontal projection plus (or minus, if acting in the opposite direction) the weight of the fluid block.

The magnitude of the resultant hydrostatic force acting on the curved surface is

The tangent of the angle it makes with the horizontal is

By taking a moment around an appropriate point, the exact location of the resultant force's line of action (e.g., its distance from one of the curved surface's end points) can be calculated. These considerations apply to all curved surfaces, whether they are above or below the liquid. Because they act in different directions, the weight of the liquid is removed from the vertical component of the hydrostatic force when a curved surface is above a liquid.

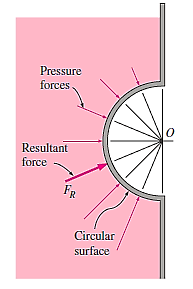
The resultant hydrostatic force acting on the surface always flows through the centre of the circle when the curved surface is a circular arc (whole circle or any part of it). This is due to the fact that pressure forces are normal to the surface, and all lines normal to a circle's surface pass through its centre. As a result, at the centre, the pressure forces form a concurrent force system that may be reduced to a single equivalent force.

Finally, hydrostatic forces acting on a plane or curved surface submerged in a multi-layered fluid of varying densities can be calculated by treating different parts of surfaces in different fluids as separate surfaces, calculating the force on each part, and then adding the forces using vector addition. It can be represented as for a planar surface as

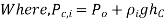
is the pressure in fluid I at the centroid of the section of the surface, and is the area of the plate in that fluid. The constraint that the moment of the equivalent force about any point equals the total of the moments of the individual forces about the same point can be used to establish the equivalent force's course of action.

Q3) Explain the concept of buoyancy.

A3)

It's a frequent observation that an object in a liquid seems lighter and weighs less than it does in air. This can be easily shown by using a waterproof spring scale to weigh a heavy object in water. Floating on water are also things made of wood or other light materials. These and other findings indicate that a fluid exerts an upward force on a body submerged in it. The buoyant force, indicated by the letter , is a force that tends to lift the body.

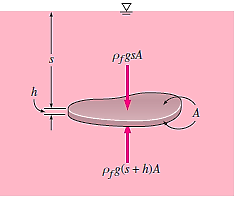
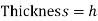
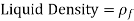
The area of the top (and bottom) surface of the plate is A, and its distance to the free surface is s.

The pressures at the top and bottom surfaces of the plate are,

The difference between these two forces is a net upward force, which is the buoyant force,

The weight of the liquid displaced by the plate equals the buoyant force exerted on it. It's worth noting that the buoyant force is independent of the body's distance from the free surface. It is also unaffected by the solid body's density.

The relationship was created for a simple geometry, but it applies to any body, regardless of shape. This can be demonstrated mathematically using a force balance, or simply by using the following logic: Consider a randomly shaped solid body submerged in a fluid at rest and contrast it with a fluid body of the same shape depicted by dotted lines at the same distance from the free surface.

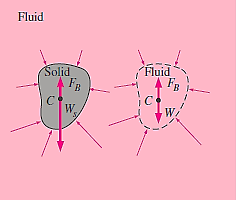
The buoyant forces acting on these two entities are the same because the pressure distributions at their boundaries, which are only dependent on depth, are the same. The net force and net moment exerted on the imaginary fluid body are zero because it is in static equilibrium. As a result, the upward buoyant force must equal the weight of the imaginary fluid body whose volume equals the solid body's volume. To achieve a zero moment, the weight and the buoyant force must have the same line of action. This is known as Archimedes’ principle.

“The buoyant force acting on a body immersed in a fluid is equal to the weight of the fluid displaced by the body, and it acts upward through the centroid of the displaced volume.”

Q4) Explain the concept of floating bodies.

A4)

The weight of the entire body must be equal to the buoyant force, which is the weight of the fluid whose volume is equal to the volume of the floating body's submerged component.

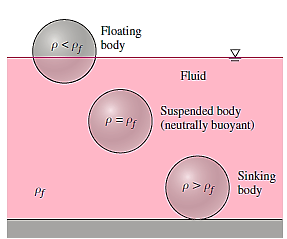
As a result, the submerged volume percentage of a floating body equals the ratio of the body's average density to the fluid's density. The floating body becomes entirely immersed when the density ratio is equal to or greater than one.

It follows from these discussions that a body immersed in a fluid

• Remains at rest at any point in the fluid when its density is equal to the density of the fluid.
• Sinks to the bottom when its density is greater than the density of
• The fluid.
• Rises to the surface of the fluid and floats when the density
• Of the body is less than the density of the fluid.

Because the buoyant force is related to the fluid's density, one might assume that the buoyant force exerted by gases like air is insignificant. This is true in general, but there are a few notable outliers.

The rise of warm air in a cooler environment, and hence the onset of natural convection currents, the rise of hot-air or helium balloons, and air motions in the atmosphere are all dominated by the buoyancy effects in gases. A helium balloon, for example, will rise due to the buoyancy effect until it reaches an altitude where the density of air (which drops with altitude) matches the density of helium in the balloon—assuming the balloon does not burst before then and the weight of the balloon's skin is ignored.

In modern geology, Archimedes' concept is applied by considering the continents to be floating on a sea of magma.

Q5) Explain the concept of Stability of a submerged body.

A5)

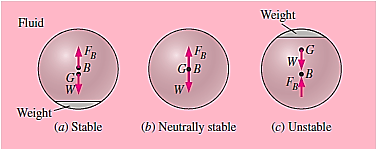
The relative locations of the body's centre of gravity G and the centre of buoyancy B, which is the centroid of the displaced volume, determine the rotational stability of an immersed body. If the body is bottom-heavy, and thus point G is directly below point B, an immersed body is stable. In such instances, a rotational disruption of the body causes a restoring moment, which allows the body to return to its original stable position. In order to move the weight to the bottom as much as possible, a stable submarine design demands for the engines and crew cabins to be situated in the lower half.

Because the cage that carries the load is at the bottom in hot-air or helium balloons (which can be considered as being immersed in air) are also stable. A submerged body with its centre of gravity G directly above point B is unstable, and any disturbance will force it to flip over. G and B must coincide for a body to be neutrally stable. This is true for bodies with a consistent density throughout. There is no inclination for such bodies to topple or right themselves.

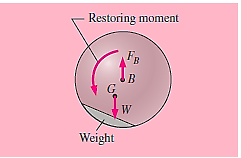
It cannot be at rest if the centre of gravity is not vertically aligned with the centre of buoyancy; it will spin toward its stable state even if no disturbance occurs.

In the figure above, the restoring moment is counter-clockwise, causing the body to rotate counter-clockwise, aligning point G vertically with point B. Although there may be some oscillation, the body eventually settles into a stable equilibrium state.

Q6) Explain the concept of Stability of a Floating body

A6)

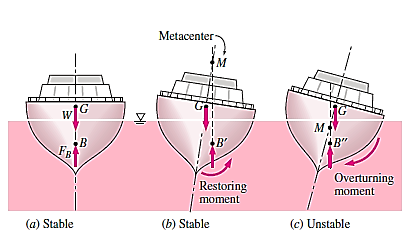
For floating bodies, the rotational stability conditions are similar. The body is always stable if the floating body is bottom-heavy and hence the centre of gravity G is directly below the centre of buoyancy B. A floating body, unlike immersed bodies, may be stable when G is exactly above B. This is because, during a rotational disturbance, the centroid of the displaced volume shifts to the side to a location , while the body's centre of gravity G remains intact.

These two forces form a restoring moment and return the body to its original position if point 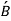,  is far enough away. The metacentric height GM, which is the distance between the centre of gravity G and the metacentre M—the junction locations of the lines of action of the buoyant force through the body before and after rotation—is a measure of floating body stability. For minor rolling degrees up to around 20°, the metacentre can be regarded a fixed position for most hull forms.

If point M is above point G, and thus GM is positive, a floating body is stable; if point M is below point G, and thus GM is negative, it is unstable. The weight and buoyant force acting on the tilted body produce an overturning moment rather than a restoring moment in the later situation, causing the body to capsize. The length of the metacentric height GM above G indicates the floating body's stability: the longer it is, the more stable it is.

Q7) What is meta centre.

A7)

When a floating body is tilted by a slight degree, it begins to oscillate around the point where the body is slanted.

The point at which the line of action of the force of buoyancy meets the normal axis of the body when the body is given a modest rotational displacement is also known as the meta-centre

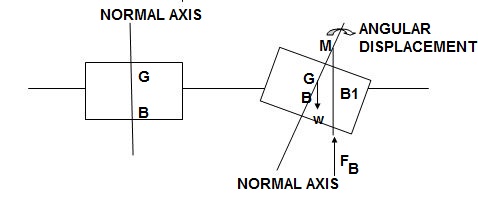
Consider a body that is afloat in a liquid. Assume the body is in equilibrium, with G representing the centre of gravity and B representing the centre of buoyancy.

As indicated in fig. 1, give the body a modest angular displacement in the clockwise direction. The centre of buoyancy, which is the centre of the displaced liquid or the centre of gravity of the body section submerged in liquid, will be shifted right from the normal axis.

As indicated in Figure, place it at B1. According to M, the line of action of the buoyancy force will intersect the normal axis of the body at some point in this posture. Meta-centre is the name given to this point M.

Q8) Find Resultant force and centre of pressure on a vertical plane surface immersed in a liquid

A8)

Consider a thin horizontal strip of the surface of thickness dx and breadth b.

Let the depth of the strip be x.

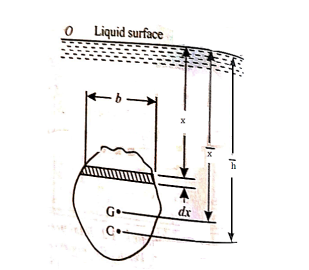
Let the intensity of pressure on strip be p.

Total pressure on the strip

Total pressure on the whole area

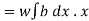
But = Moment of the surface area about the liquid level = A

Moment of the pressure about free surface

Total Moment,

But = Moment of inertia of the surface about free surface OO (I0)

Hence, M = wI0

The sum of the moment of the pressure is also equal to P×.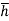

But

Above equation becomes

Q9) Find Resultant force and centre of pressure on a inclined plane surface immersed in a liquid

A9)

Let A = area of the surface

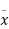= depth of the centre of gravity from the free liquid surface.

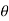=angle at which the immersed surface is inclined with the liquid surface.

w=specific weight of liquid.

Consider a strip of thickness dx width b at a distance l from O.

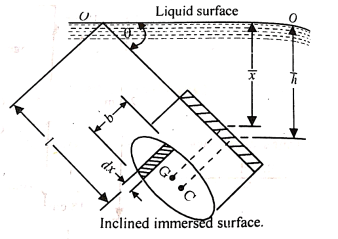
The intensity of pressure on the strip

Total pressure on the surface

But Moment of surface about OO

Let, = Depth of centre of pressure below free liquid surface

IG = Moment of inertia of the immersed surface about 00.

Moment of pressure about OO

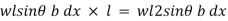
Sum of moments about O

But = I0 = Moment of inertia of the surface about point O

Sum of moment of all such pressure about O is also equal to

Were,

Q10) A rectangle plane surface is 2 m wide & 3 m deep. It lies in vertical plane in water. Determine the total pressure & position of centre of pressure when its upper edge is horizontal & a) Coincides with water surface  b) 2.5 m below the free water surface.

A10)

 Given

b = 2m

d = 3m

a). Upper edge coincides with water surface

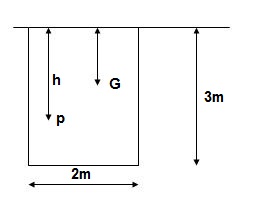
A = b x d = 2 x 3 = 6 m2

X = d/2 -3/2 = 1.5 m

Total Pressure

F = AX

= 9810 x 6 x 1.5

= 88290 N

IG = bd3/12 = 2 x 33/12 = 4.5 m4

Centre of Pressure

h = IG/AX + X = 4.5/ (6 x 1.5) + 1.5 = 2m

b). Upper edge 2.5 m below water surface

X = 2.5 + 3/2 = 4m

Total pressure F = Ax

= 9810 x 6 x 4

= 235440 N

h = IG/AX + X = 4.5/ (6 x 4) + 4 = 4.1875 m

Q11) Consider a large car submerged in water in a flat-bottomed lake. The car's driver's side door is 1.1 metres high and 0.9 metres wide, with the top edge of the door 8 metres below the water's surface. If (a) the automobile is well-sealed and contains air at atmospheric pressure and (b) the car is filled with water, calculate the net force acting on the door (normal to its surface) and the location of the pressure centre.

A11)

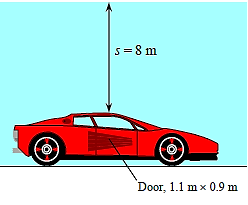
When the car is well-sealed and thus the pressure inside the car is the atmospheric pressure, the average pressure on the outer surface of the door is the pressure at the centroid (midpoint) of the surface, and is determined to be,

Then the resultant hydrostatic force on the door becomes

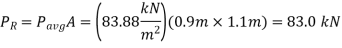
The pressure center is directly under the midpoint of the plate, and its distance from the surface of the lake is determined to be,

When the car is filled with water, the net force normal to the surface of the door is zero since the pressure on both sides of the door will be the same.

Q12) As shown, an automatic gate is made out of a long, solid cylinder with a radius of 2 feet that is hinged at point A. The cylindrical gate opens by twisting around the hinge at point A when the water level exceeds 15 feet. When the gate opens, calculate (a) the hydrostatic force acting on the cylinder and its line of action, and (b) the cylinder's weight per ft length.

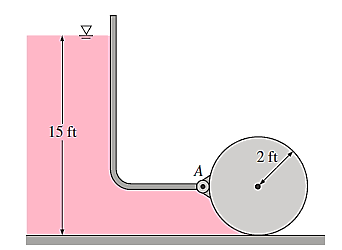
A12)

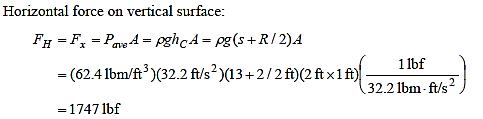
When the water level is 15-ft high, the gate opens and the reaction force at the bottom of the cylinder becomes zero.

Then the forces other than those at the hinge acting on the cylinder are its weight, acting through the centre, and the hydrostatic force exerted by water. Taking a moment about the point A where the hinge is and equating it to zero gives

Q13) The water side of a 100-meter-long dam's wall is a quarter circle with a radius of 10 metres. When the dam is full to the rim, calculate the hydrostatic force on the dam and its path of action.

A13)

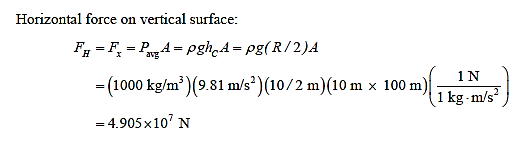
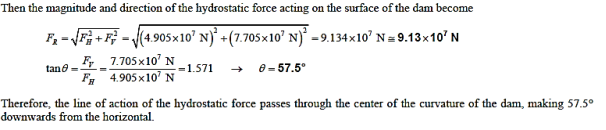
Q14) A 5-foot-wide L-shaped gate hinged at point A controls the flow of water from a reservoir. Determine the mass of the needed weight W if the gate is to open when the water level is 12 feet.

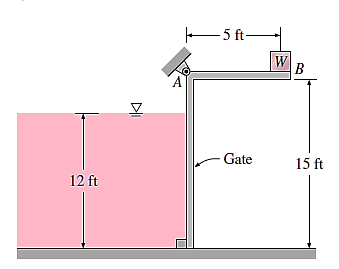
A14)

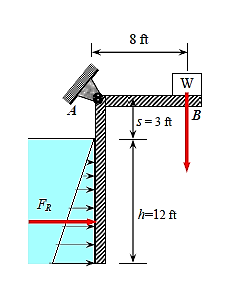
The average pressure on a surface is the pressure at the centroid (midpoint) of the surface, and is determined to be,

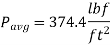
Then the resultant hydrostatic force acting on the dam becomes,

The line of action of the force passes through the pressure centre, which is 2h/3 from the free surface,

Taking the moment about point A and setting it equal to zero gives,

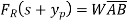
Q15) A 5-foot-wide L-shaped gate hinged at point A controls the flow of water from a reservoir. Determine the mass of the needed weight W if the gate is to open when the water level is 8 feet.

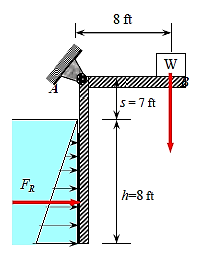
A15)

The average pressure on a surface is the pressure at the centroid (midpoint) of the surface, and is determined to be,

Then the resultant hydrostatic force acting on the dam becomes,

The line of action of the force passes through the pressure centre, which is 2h/3 from the free surface,

Taking the moment about point A and setting it equal to zero gives,

Q16) An antique 1-cm-diameter cylindrical hydrometer with entirely wiped-out division marks is used to determine the density of a liquid. First, the hydrometer is submerged in water and the water level is recorded. After dropping the hydrometer into the other liquid, it's noticed that the water mark has risen 0.5 cm above the liquid–air contact. Calculate the density of the liquid based on the height of the water mark, which is 10 cm.

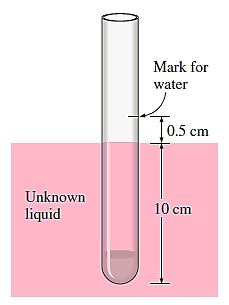
A16)

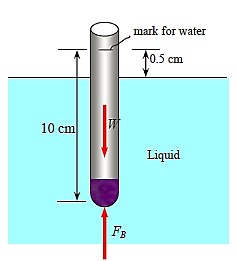
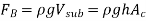
In pure water,

In the liquid,

Setting the relations above equal to each other (since both equal the weight of the hydrometer) gives,

Q17) For an underwater construction project, a crane is utilised to lower weights into a lake. Determine the strain in a crane's rope caused by a 3-foot-diameter spherical steel block (density = 494 lbm/ft3) hung in the air and entirely submerged in water.

A17)

Assumptions

1 The buoyancy force in air is negligible.

2 The weight of the rope is negligible

The forces acting on the concrete block in air are its downward weight and the upward pull action (tension) by the rope. These two forces must balance each other, and thus the tension in the rope must be equal to the weight of the block:

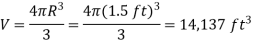
When the block is immersed in water, there is the additional force of buoyancy acting upwards. The force balance in this case gives,

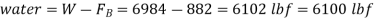
Q18) A spring scale is used to determine the volume and average density of an irregularly shaped body. In air, the body weighs 7200 N while in water, it weighs 4790 N. Calculate the volume and density of the human body. Make a list of your assumptions.

A18)

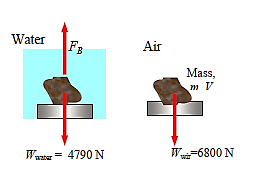
Assumptions

1 The buoyancy force in air is negligible.

2 The body is completely submerged in water.

The mass of the body is,

The difference between the weights in air and in water is due to the buoyancy force in water,

As,

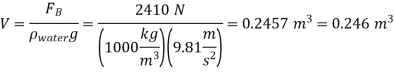
Then the density of the body becomes

Q19) A triangular plate of 1m base & 1.5 m altitude is immersed in water. The plate is inclined at 300 with free water surface & base is parallel to & at a depth of 2 m from water surface. Find total pressure &centre of pressure.

A19)

 Given       

b = 1 m

h = 1.5 m

 = 300

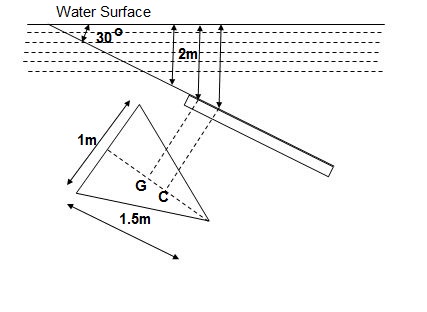
A = ½ x b x h = ½ x 1 x 1.5 = 0.75 m2

X = 2 + 1.5/3 x Sin 30 = 2.25 m

F = AX

= 9810 x 0.75 x 2.25

= 16.55 x 103 N

IG = bh3/36 = 1 x 1.53/36 = 0.09375 m4

h = IGSin2/AX + X

= 0.09375 x (Sin 30)2/0.75 x 2.25 + 2.25

= 2.264 m

Q20) A solid cylinder of diameter 4m and height 4 m. Find the metacentric height of the cylinder if the specific gravity of cylinder is 0.6 and it is floating in water with its axis vertical. State whether the equilibrium is stable or unstable.

A20)

 Given 

D=4m

H=4m

S=0.6

Depth of cylinder in water = 0.6H = 0.6(4) = 2.4m

Distance of centre of buoyancy(B) from A

AB = 2.4 / 2 = 1.2m

Distance of centre of gravity (G) from A

AG = H / 2 = 2m

BG = AG – AB = 2 – 1.2 = 0.8m

I = 4

V = Volume of cylinder in water

=

Metacentric height GM = (I / V) – BG

= (12.56/30.16) – 0.8

= -0.383 m

Negative sign means that the metacentre M is below the centre of gravity G. Thus, the cylinder is in unstable equilibrium.