Unit - 5

Dimensional Analysis and Similarities

Q1) Explain Dimensional homogeneity with any suitable example.

A1)

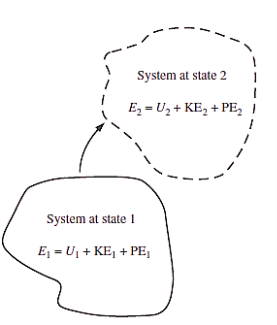
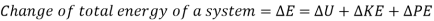
Now LHS,

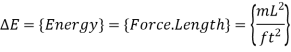
Now RHS,

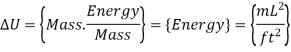
If we find ourselves in a situation where two additive terms in an equation have different dimensions at some point throughout the analysis, this is a clear indication that we made an error earlier in the process.

Calculations are valid only when the units are also homogeneous in each additive term, in addition to dimensional homogeneity.

Q2) Explain the use of dimensionless numbers in experimental investigation.

A2)

In several domains of engineering, dimensional less numbers are collections of variables that provide order-of-magnitude estimations of a system's behaviour.

• In engineering, dimensionless numbers are frequently employed to capture underlying phenomena and scale up.
• Dimensionless numbers lower the number of variables that represent a system, minimising the amount of experimental data needed to make scalable system correlations from physical occurrences. The Reynolds number is the most common dimensionless group in fluid dynamics (Re).
• It is feasible to determine whether particular effects or forces are important or can be safely ignored in the model by studying dimensionless numbers.
• It demonstrates whether certain effects or forces may be safely ignored.
• It enables us to adapt the force correlations discovered in a specific (experimentally convenient) system to a considerably broader class of multiphase flow issues.

Now let's look at how to make the nondimensional parameters, or π. There have been various methods devised for this goal, but the most popular (and easiest) one is Edgar Buckingham's (1867–1940) method of repeating variables. In 1911, Russian physicist Dimitri Riabouchinsky (1882–1962) described the approach for the first time. This method can be thought of as a "recipe" or step-by-step procedure for producing nondimensional parameters.

Q3) Explain Geometric, Dynamic & Kinematic similarity.

A3)

We first describe the basic notion of dimensional analysis—the principle of similarity—before moving on to the practise of dimensional analysis.

For perfect likeness between a model and a prototype, three conditions must be met. The first requirement is geometric similarity—the model must have the same shape as the prototype, but it can be scaled by a constant amount. The second criteria is kinematic similarity, which requires that the velocity at each location in the model flow be proportional to the velocity at the corresponding position in the prototype flow (by a constant scale factor).

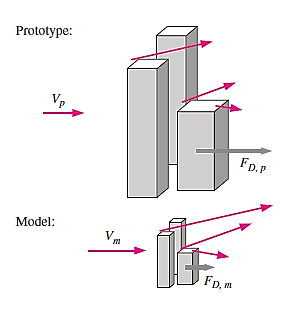
The velocity at corresponding sites must scale in magnitude and point in the same relative direction for kinematic similarity. Geometric similarity can be thought of as length-scale equivalent, whereas kinematic similarity can be thought of as time-scale equivalence. Kinematic similarity is dependent on geometric similarity. The velocity scale factor, like the geometric scale factor, can be less than, equal to, or greater than one.

The geometric scale factor for image above is less than one (model is smaller than prototype), while the velocity scale is bigger (velocities around the model are greater than those around the prototype).

Dynamic similarity is the third and most restricted similarity condition. When all forces in the model flow scale by a constant factor to equivalent forces in the prototype flow, dynamic similarity is obtained (force-scale equivalence). Forces have a scale factor that can be less than, equal to, or greater than one, just like geometric and kinematic similarity.

For image above, the force-scale factor is less than one since the force on the model building is less than that on the prototype.

Dynamic similarity requires, but is not sufficient for, kinematic similarity. A model flow and a prototype flow can therefore attain geometric and kinematic similarity, but not dynamic similarity. For complete similarity to be guaranteed, all three-similarity criterion must be met.

“Complete resemblance between a model and prototype in a general flow field is only accomplished when there is geometric, kinematic, and dynamic similarity.”

Q4) Explain Reynolds model laws.

A4)

In flow situations where in addition to inertia, viscous force is the other predominant force, the similarity of flow in the model and its prototype can be established if Reynolds number is same for both the systems.

This is known as Reynolds law and according to this law,

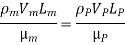
Where, ρm = density of fluid in model

Vm = velocity of fluid in model,

Lm = length of linear dimension of the model, and

µm = viscosity of fluid in model

And ρ P, VP, LP and µP are the corresponding values of density, velocity, linear dimension and viscosity of fluid in prototype.

Following are some of the phenomena for which Reynolds model law can be a sufficient criterion for similarity of flow in the model and the prototype:

• Motion of airplanes,
• Flow of incompressible fluid in closed pipes,
• Motion of submarines completely under water, and
• Flow around structures and other bodies immersed completely under moving fluids.

Q5) Explain Froude model laws.

A5)

When the gravitational force can be the only predominant force which controls the motion in addition to the inertia force, the similarity of the flow in any two such systems can be established if the Froude’s number of both the systems is the same.

This is known as Froude’s Model Law.

Some of the phenomenon for which the Froude Model Law can be sufficient criterion for dynamic similarity to be established in the model and the prototype are:

• Free surface flows such as flow over spillways, sluices, etc.
• Flow of jet from an office or nozzle.
• Where waves are likely to be formed on the surface.
• Where fluids of different mass densities flow over one another

Let, Vm = velocity of fluid in model

Lm = length (or linear dimension) of the model

gm = acceleration due to gravity (at a place where model is tested)

And VP, LP and gP are the corresponding values of the velocity, length and acceleration due to gravity for the prototype.

Then according to Froude Law,

(Fr)m = (Fr)P

As the value of g at the site of mode testing will be practically the same as at site of the               proposed prototype, therefore gm = gP and the equation 1 values as

Where Lr = scale ratio for length

The law of Froude's model is applied

• Free local flow such as streaming to spill, heirs, sluices, channels etc.
• Flow of the jet from the orifice or nozzle
• Where waves may form more
• When a flow of liquid of different strength passes one anther

Q6) Explain Euler model laws.

A6)

Euler's model law states that models should be designed on Euler's number, which means that the Euler number for the model and prototype should be same for dynamic similarity. When the pressure forces alone predominate in addition to the inertia force, Euler's model law applies.

Q7) Explain Undistorted and Distorted Models.

A7)

Undistorted Model:

Undistorted models are ones that are geometrically identical to their prototypes, or in other words, if the scale ratio between the model's linear dimensions and its prototype is the same. The results of the undistorted model can easily anticipate the behaviour of the prototype.

Distorted Model:

If a model is not geometrically identical to its prototype, it is said to be distorted. Different scale ratios for the linear dimensions are used for a distorted model. For rivers, harbours, and reservoirs, for example, two separate scale ratios are used, one for horizontal dimensions and the other for vertical dimensions. As a result, models of rivers, harbours, and reservoirs will be warped. If the horizontal and vertical scale ratios for the river are taken to be the same so that the model is undistorted, the depth of water in the river model will be extremely small, making it difficult to measure precisely.

Advantages:

• The model's vertical dimensions can be precisely measured.
• The model's cost can be decreased.
• The model's turbulent flow can be maintained.

Although the distorted model has several advantages, the outcomes of the distorted model cannot be simply translated to the prototype. However, occasionally highly relevant information can be gleaned from distorted models.

Scale Ratio for Distorted Models:

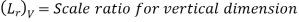
Scale ratio for Velocity:

Scale ratio for area of flow:

Scale ratio for discharge:

Q8) Write Weber model laws & Mach model laws.

A8)

Weber model laws

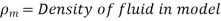
Used in:

• Capillary rise in narrow passages
• Capillary movement of water in soil
• Capillary waves in channel
• Flow over weirs for small heads

Mach model laws

Models are designed on Mach number, which is the square root of the ratio of a flowing fluid's inertia force to its elastic force. The dynamic similarity is obtained by:

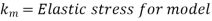
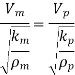
Used in:

• Flow of aeroplane and projectile through air at supersonic speed
• Aerodynamic testing
• Under water testing of torpedoes
• Water hammer

Q9) Explain Rayleigh's method.

A9)

This method is used to find the expression for a variable that is dependent on no more than three or four variables. When the number of independent variables exceeds four, finding an expression for the dependent variable becomes quite difficult.

Let X is a variable, which depends on

Mathematically it is written as,

It can also be written as,

Where K = constant

a, b, c, are arbitrary Powers

Example: The length (L) of a pendulum and the acceleration due to gravity determine the time-period (t) of the pendulum ( g). Determine a time-period expression.

Sol:

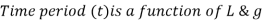
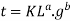
Substituting the dimensions on both sides,

Equating the powers of M, L and T on both sides, we have

Substituting the values,

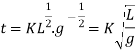
The value of K is determined from experiments which is given as,

Q10) Explain Buckingham π-theorem.

A10)

When the number of variables exceeds the number of fundamental dimensions, Rayleigh's approach of dimensional analysis becomes more difficult (M, L, T). Buckingham's pie theorem states, "This difficulty can be overcome by using Buckingham's pie theorem." When a physical phenomenon has n variables (independent and dependent variables) and these variables have m fundamental dimensions (M, L, T), the variables are arranged into (n -m) dimensionless terms. Each term is referred to as a "pie-term."

Mathematically it is written as,

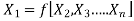
Each of π-terms is dimensionless and is independent of the system. Division or multiplication by a constant does not change the character of the π-term. Each π-term contains m + 1 variables, where m is

The number of fundamental dimensions and is also called repeating variables.

Each π term is written as,

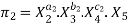
Each equation is solved by the principle of dimensional homogeneity and values of etc., are obtained. Obtained values are substituted in above equation.

The values of π obtained is then substituted in function equation.

The final equation for the phenomenon is obtained by expressing any one of the π-terms as a function of others as

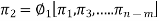
Q11) Write the primary dimensions of each of the following variables from the field of thermodynamics, showing all your work: (a) energy E; (b) specific energy e = E/m; (c) power W

A11)

Energy,

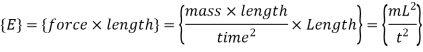
Specific energy,

Power,

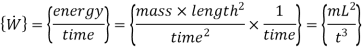
Q12) Newton’s second law is the foundation for the differential equation of conservation of linear momentum. In terms of the material acceleration following a fluid particle, we write Newton’ second law as follows

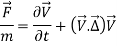
Write the primary dimensions of each additive term in the

Equation, and verify that the equation is dimensionally homogeneous.

Show all your work.

A12)

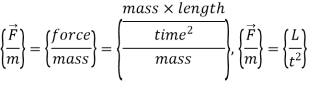
Q13) For a design competition, a student team will create a human-powered submarine. The prototype submarine's overall length is 2.24 metres, and its student designers anticipate that it will be able to go fully submerged under water at a speed of 0.560 metres per second. At T = 15°C, the water is freshwater (a lake). The design team creates a one-eighth scale model to test in the wind tunnel at their institution. The drag balance strut is surrounded by a shield, which prevents the strut's own aerodynamic drag from influencing the measured drag. The wind tunnel has a temperature of 25°C and a pressure of one standard atmosphere. To achieve resemblance, what air speed do they need to run the wind tunnel at?

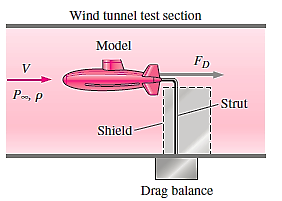
A13)

For water at, 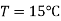and atmospheric pressure and .

For air, and atmospheric pressure and .

Q14) For military use, a lightweight parachute is being developed. It has a diameter of 24 feet and a total weight of 230 lbf, including the dropping payload, parachute, and equipment. At this weight, the parachute's design terminal settling speed Vt is 20 ft/s. In a wind tunnel, a one-twelfth scale model of the parachute is tested. The temperature and pressure in the wind tunnel are identical to those in the prototype, namely 60°F and standard atmospheric pressure.

(a)  Determine the prototype's drag coefficient. (Hint: At terminal settling speed, aerodynamic drag balances weight.) (b) At what wind tunnel speed should the wind tunnel be run for dynamic similarity to be achieved? c) In the wind tunnel, calculate the model parachute's aerodynamic drag (in lbf).

A14)

For air at, and atmospheric pressure and

Drag coefficient,

As, if the fluid is the same and dynamic similarity between the model and the prototype is achieved, the aerodynamic drag force on the model is the same as that on the prototype, thus,

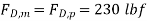
Q15) There are some pressurised wind tunnels. Discuss why a research organisation would go to such great lengths and spend so much money to pressurise a wind tunnel. What factor will the Reynolds number increase by if the air pressure in the tunnel increases by a factor of 1.5, all other factors being similar (same wind speed, same model, etc.)?

A15)

It is often difficult to achieve a high-enough wind tunnel speed to match the Reynolds number between a small model and a large prototype. Even if we were able to match the speed, the Mach number would often be too high. A pressurized wind tunnel has higher density air. At the same Reynolds number, the larger density leads to a lower air speed requirement. In other words, a pressurized wind tunnel can achieve higher Reynolds numbers for the same scale model. If the pressure were to be increased by a factor of 1.5, the air density would also go up by a factor of 1.5 (ideal gas law), assuming that the air temperature remains constant. Then the Reynolds number, Re = ρVL/μ, would go up by approximately 1.5. Note that we are also assuming that the viscosity does not change significantly with pressure, which is a reasonable assumption

Q16) Some pupils desire to envision flow while watching a baseball spin in the air. Because their fluids lab has a lovely water tunnel into which they can inject rainbow dye streaklines, they decide to test a spinning baseball in it. To achieve similarity, they must match both the Reynolds and Strouhal numbers between their model test and the actual baseball, which travels at 80 miles per hour and spins at 300 rpm. Both the air and the water are at a temperature of 20°C. What speed should the water in the water tunnel be run at, and what rpm should the baseball be spun at?

A16)

For air at, and atmospheric pressure and .

For water, 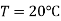and atmospheric pressure and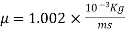

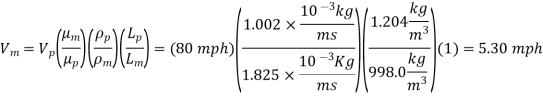
Strouhal number, as is proportional to f

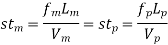
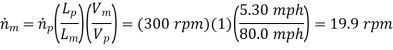
Q17) From the following data, find the scale ratio of model Velocity of water 1 m/'s through circular pipe. Prototype: Velocity of oil 0.12 ms through 50 mm diameter pipe. Assume kinematic viscosity of water 0.01 cms and that of oil 0.008 cm/s. Assume dynamic similarity.  Also find the diameter of pipe used for model.

A17)

Prototype

Vp -012 m/s

Dp = 50mm = 0.05 m

Vp = 0.006 cm²/sec

Model

Vm= 1m/s

Dm=?

Vm= 0.01 cm^2/sec

To find:

Since it is pipe flow, Reynold's ember mast be applied

Model scale ratio is 1:5

Now, diameter of model pipe

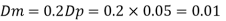
Q18) A ship has a length of 150 m and wetted area 3000 m² A model of this ship 5 m in length when towed in fresh water (p= 1000 kg/m) at 2 m/s produces a resistance of 40N. Calculate (1) corresponding speed of the ship. (i) the shaft power required to propel the ship at this speed through sea water (p=1030 kg/m). Take the propeller efficiency as 75%

A18)

Model

Lm= 5 m

Vm= 2 m/s

Fm = 40 N

Prototype

Lp= 150 m

Ap= 3000m^2

Propeller efficiency= n= 75 %

To find:

Speed of ship Vp

Since it is ship motion Reynolds number must be applied

Ratio of drag force

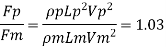
Drag force on prototype

Actual power input

Q19) The performance of a spillway is to be studied by means of a model constructed to a scale of 1:9. Determine: (1) Rate of flow in the model for a prototype discharge of 1400 m/s. (2) Energy lost in the prototype if the energy loss in model is 0.3 kW

A19)

Scale of model 1:9

Lr = 9

Discharge of prototype Q = 1400 m^3 /s

Since it is a spillway, Froude number must be applicable.

Using discharge scale ratio

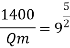
Energy loss

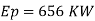
Q20) A ship model of scale 1/60 is towed through sea water at a speed of 1:1 m/s A force of 2.1 N is required to tow the model. Determine the speed of ship and the propulsive force on the ship if the prototype is subjected to wave resistance only.

A20)

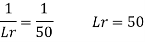
Speed of model Vm=1.1 m/s

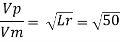
Resistance to prototype in sea water