Unit - 6

Viscous Flow

Q1) Derive Hagen Poiseuille formula.

A1)

The velocity distribution throughout a segment, the ratio of maximum velocity to average velocity, the shear stress distribution, and pressure drop for a given length must all be determined for the flow of viscous fluid via circular pipe. If the Reynolds number (Re *) is less than 2000, the flow through the circular pipe will be viscous or laminar.

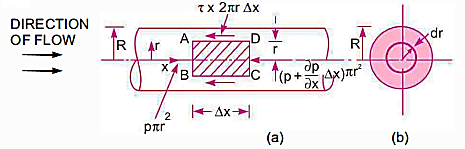
Pressure Intensity on Face AB

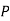
Pressure on Face CD

Pressure force on Face AB

Pressure force on Face CD

Shear force on the surface of fluid element

As, there is no acceleration, hence the summation of all forces in the direction of flow must be zero,

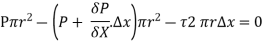
Velocity Distribution:

In this equation, the distance y is measured from the boundary. The radial distance r is related to distance y by the relation.

Integrating the above equation w. r. t. ‘r’ we get

Where C is the constant of integration, and its value is obtained from the boundary conditions.

At r = R, u = 0

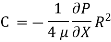
So,

Ratio of Maximum velocity to average velocity:

The velocity is maximum when r = 0

The fluid flowing per second through this elementary ring:

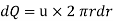
So, Average velocity,

So,

Drop of pressure for a given Length (L) of a pipe,

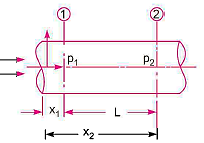
Integrating,

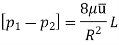
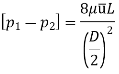
Loss of pressure head,

Q2) Derive the general equation for flow of viscous fluid between two parallel fixed plates

A2)

The shear stress distribution, velocity distribution across a segment, ratio of maximum velocity to average velocity, and pressure head differential for a certain length of parallel plates must all be computed in this scenario.

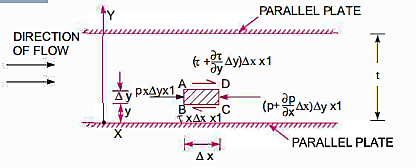
Pressure Intensity on Face AB

Pressure on Face CD

Shear stress 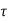acting on the face BC then the shear stress on the face AD

If the width of the element in the direction perpendicular to the paper is unity, then the forces acting on the fluid element are:

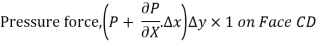
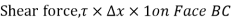
So,

There is no acceleration in a steady and uniform flow, hence the resultant force in the flow direction is zero.

Q3) What is the power absorbed in Footstep Bearing?

A3)

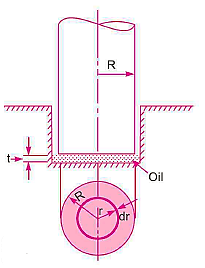
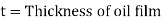
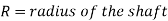
Area of the elementary ring,

Shear Stress,

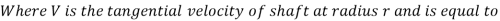
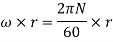
Shear force on the ring,

Torque required to overcome the viscous resistance,

Total torque required to overcome the viscous resistance

Power absorbed:

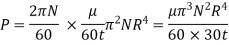
Q4) What is the power absorbed in Collar Bearing?

A4)

Collar Bearing:

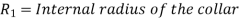
Power absorbed:

Q5) Explain Capillary Tube Method.

A5)

The viscosity of a liquid is estimated using the capillary tube method by measuring the pressure differential across a certain length of capillary tube. Calculating viscosity is done using the Hagen Poiseuille law. A constant head tank is filled with the liquid whose viscosity is to be determined. The liquid is kept at a constant temperature and permitted to travel from the constant head tank through the capillary tube. The liquid is then collected in a measuring tank for a set period of time. The rate at which liquid is gathered in the tank per second is then calculated. The pressure head, abbreviated as 'h,' is measured at a distance from the tank.

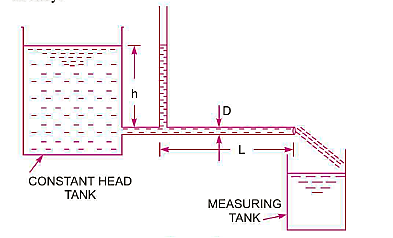
The pressure at outlet is atmospheric

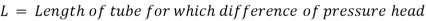
Using Hagen Poiseuille's Formula,

But,

So,

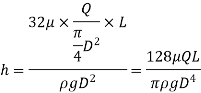
Q6) Explain falling sphere method.

A6)

Falling sphere method of measuring viscosity of a liquid is based on Stokes law. A small spherical ball is released into the liquid to be tested and it accelerate under the gravitational force until it reaches a maximum terminal velocity V when the buoyant and viscous drag forces balance the gravity force.

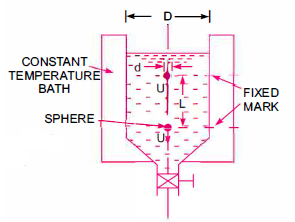
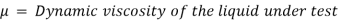
The force acting on the sphere are-

1)     Weight W, acting vertically downward.

2)     Buoyant force FB, acting vertically upward

3)     Drag force FD, acting vertically upward.

W= volume × Density of sphere × g

FB = weight of liquid displaced

= volume of liquid displaced × density of liquid × g

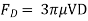
For equilibrium

Q7) Explain rotating cylinder methos.

A7)

In this method, Newton’s law of viscosity is used to measure the viscosity of a fluid.

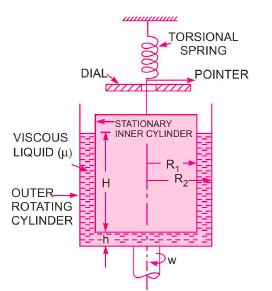
It consists of two concentric cylinders, the annular space between them is filled with the liquid whose viscosity is to be determined.  The outer cylinder is rotated at a constant angular velocity with respect to the inner stationary cylinder. The torque transmitted by the enclosed liquid to the stationary cylinder is measured by the torsional strain of the restraining spring attached to the top of the inner cylinder.

According to Newton’s law of viscosity,

Since the annular space t = (R2 – R1) is quite small (where R2 and R1 are the radii of the outer and inner cylinders respectively), the velocity gradient

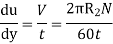
(Where N= the rotational speed of the outer cylinder in rpm)

(Where h = height of liquid)

Viscous torque = Viscous drag x radius

Viscous torque must be equal to the torque T exerted by the torquemeter.

Q8) Derive Darchy-Weish-Bach Equation.

A8)

The velocity of the liquid layer adjacent to the pipe wall is zero when a liquid flows through a pipe. Due to viscosity, the velocity of the liquid increases as it approaches the wall, causing a velocity gradient and hence shear forces throughout the liquid. This viscous movement results in energy loss, which is commonly referred to as frictional loss.

William Froude developed the following fluid fraction laws for turbulent flow based on his experiments.

The frictional resistance for turbulent flow is:

• Proportional to where n fluctuates between 1.5 and 2.0
• Proportional to fluid density
• Proportional to the area of the surface in contact
• Independent of pressure
• Dependant on the type of the surface in touch

Expression for Loss of Head Due to Friction in Pipes:

Consider a uniform hori­zontal pipe, having steady flow

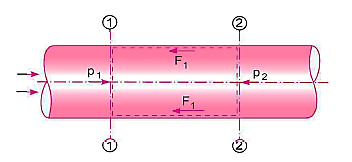
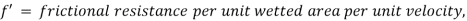
Applying Bernoulli's equations between sections 1-1 and 2-2,

Total head at 1-1 = Total head at 2-2 + loss of head due to friction between 1-1 and 2-2.

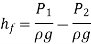
But is the head lost due to friction and hence intensity of pressure will be reduced in the direction of flow by frictional resistance

Now,

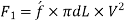
The forces acting on the fluid between sections 1-1 and 2-2 are

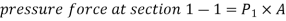
Resolving all forces in the horizontal direction, we have

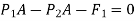
But,

So,

Putting,

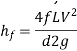
This is known as Darchy-Weish-Bach Equation

Q9) A horizontal circular pipe with a diameter of I 00 mm and a length of IO m is carrying crude oil with a viscosity of 0.97 poise and a relative density of 0.9. Calculate the pressure differential between the pipe's two ends if I00 kg of oil is gathered in a tank in 30 seconds.

A9)

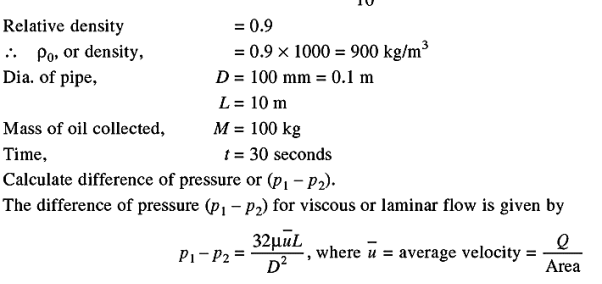
Q10) A circular pipe with a diameter of 50 mm and a length of 300 m is filled with an oil with a viscosity of 0.1 Ns/m2 and a relative density of 0.9. The fluid flow rate through the pipe is 3.5 litres per second. Determine the pressure drop throughout a 300-meter length of pipe, as well as the shear stress at the pipe wall.

A10)

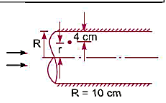
Q11) In a pipe with a diameter of 200 mm, a laminar flow is occurring. 1.5 mis is the maximum velocity. Calculate the mean velocity and radius at which this happens. Calculate the velocity at a distance of 4 cm from the pipe's wall.

A11)

Mean velocity,

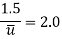
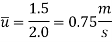
Radius at which 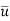occurs,

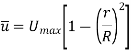
The radius r at which,

So,

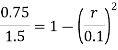
Velocity at 4 cm from the wall,

The velocity at a radius = 0.06 m or 4 cm from pipe wall is ,

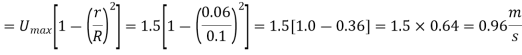
Q12) Calculate the following: I the axe pressure 2 gradient along flow, (ii) the average velocity, and (iii) the discharge for an oil with a viscosity of 0.02 Ns/m flowing between two stationary parallel plates 10 mm apart. The velocity is 2 m/s in the middle of the plates.

A12)

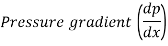
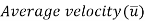
Q13) At 15°C, water flows between two big parallel plates separated by 1.6 mm. If the average velocity is 0.2 mis, calculate I the highest velocity, (ii) the pressure drop per unit length, and (iii) the shear stress at the plate walls. At 15°C, the viscosity of water is 0.01 poise.

A13)

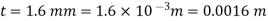
Maximum velocity,

The pressure drop,

The pressure drop per unit length,

Shear stress at the walls,

Q14) A journal bearing with a diameter of 50.15 mm and a length of 100 mm revolves centrally around a shaft with a diameter of 50 mm. Oil with a viscosity of 0.9 poise is used to fill the angular space between the shaft and the bearing. Calculate the power absorbed in the bearing when the rotational speed is 60 rpm.

A14)

Thickness

Tangential speed of shaft,

Shear stress,

Shear force,

Resistance torque,

Power,

Q15) In a 200 mm long bearing, a 100 mm diameter shaft revolves at 60 rpm. Find the power absorbed in the bearing by assuming the two surfaces are equally separated by a distance of 0.5 mm and a linear velocity distribution in the lubricating oil with a dynamic viscosity of 4 centipoises.

A15)

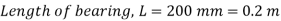
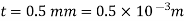
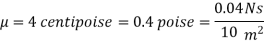
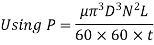
Q16) Calculate the torque necessary to rotate a vertical shaft with a diameter of 100 mm at 750 revolutions per minute. The shaft's lower end is supported by a footstep bearing. The end of the shaft and the bearing's surface are both flat, separated by a 0.5 mm thick oil film. The oil's viscosity is set to 1.5 poise.

A16)

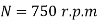
Thickness of oil film,

Torque required,

Q17) Two Pitot-Prandtl tubes are used to find the velocities at the middle and the quarter point of a circular pipe simultaneously. Find the discharge of water (Assuming turbulent flow)if the diameter of the pipe is 300 mm and readings of the tubes are 2.53 m/s and 2.29 m/s.

A17)

Diameter d = 300 mm = 0.3 m.

Velocity at middle u max=2.53 m/s at y = 0 Velocity at quarter Point of a circular pipe u = 2.29 m/s at y = 0.075

Step 1: Now for turbulent flow,

At y = 0.075

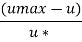
                                                                …(Eq.1)

Step 2: At y=0 u. = 3.75,

Put u* in equation 1

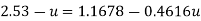
Step 3: Discharge.

Q18) For turbulent flow in circular pipe of radius 'r friction factor is 0.02 Estimate the local velocity at a radial distance 0.25 r from the axis of the pipe. If mean velocity is 0.3 m/s, what will be the velocity at the centre line of pipe?

A18)

Radius R = r,

Frictional factor f=0.02,

Radial distance 10.25 r

Mean velocity u 0.3 m/s

Step 1: By Karman-Prandtl resistance equation for rough pipe is,

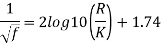
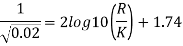
Step 2: Now using equation,

Step 3: Now for smooth and rough pipes,

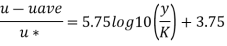
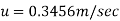
Step 4: Maximum velocity occurs at centre-line of pipe, r = 0, u = u max

Local velocity at 0.25 r from axis of pipe is 0.3455 m /s and velocity at centre line is 0.356 m/sec.

Q19) Determine the head loss in kPa for a pipe line 700 m long carrying petrol at the flow rate of 200 Lps. (p = 730 kg/m³, μ = 2.92 x 10 N-s/m²). The diameter of the pipe is 30 cm and the equivalent roughness magnitude is 0.3 mm. Use Moody's diagram.

A19)

L = 700 m long,

Q = 200 Lps= 0.2 m³/sec,

p = 730 kg/m³, μ = 2.92 x 10 N-s/m².

d = 30 cm = 0.3 m, e = 0.3 mm = 0.3 x 10³ m

Step 1: Velocity,

Step 2: Relative roughness,

Step 3: Reynolds’s number,

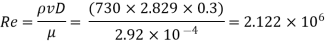
Step 4: Refer Moody's diagram and R., we get

Step 5: Head loss by Darcy's equation,

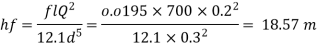
Step 6: Head loss in kPa (pressure),

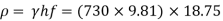
= 132.98 x 10³ mPa

p = 132.98 kPa

:. The head loss in kPa is 132.98 kPa.

Q20) Determine the head lost in a diameter 300 m, 300 m long cast iron pipe when (1) Water at 15°C flow at a velocity 15 nvs and (ii) Fuel oil at 15°C flow at the same velocity. Assume size of surface imperfection 0.244 mm. Refer Moody's diagram. Take the following properties.

A20)

L = 300 m, d = 300 mm = 0.3 m,

c = 0.244, V = 15 m/sec.

Case I: When water is flow with velocity = 15 m/sec.

e = 0.244

Step 1: Relative roughness

Step 2: Reynolds number

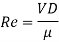
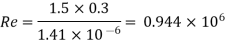
Step 3: Use moody's table for R. And values,

f = 0.0186

Step 4: Head loss by Darcy's equation,

Case II: When oil flows with same velocity 1.5 m/sec,

:. By using Moody's curve for Re and e/d values,

f = 0.0215

Head loss