Unit - 1

Fundaments- system and control volume

Q1) Explain System in thermodynamics.

A1)

System

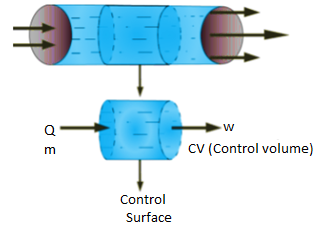
Thermodynamic system is the region or quantity of matter which is under observation for thermodynamic changes. The quantity of matter can be gas, solid, liquid.

Surroundings/ Environment

Everything which is external to the system is termed as surroundings / environment.

Boundaries

A system boundary separates system and surrounding. It can be both fixed and movable. A closed surface surrounding in a system through which energy & mass may enter or leave the system is called as Boundary.

Universe

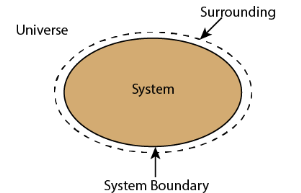
System & surrounding when combined form Universe.

Types of System

• An isolated system cannot exchange either mass or energy with the surroundings. 

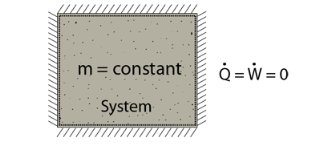
• A closed system exchanges energy with the surrounding but mass transfer is not possible. 

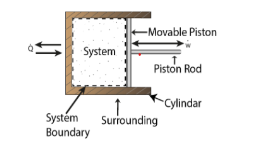
• An open system can exchange both mass and energy with the surroundings.

Q2) Explain the term property in thermodynamics.

A2)

The precise state of a substance is referred to as its state variables, which determine the state of a substance are referred to as its properties or parameters.

Internal energy, pressure, temperature, and volume Enthalpy, entropy, and heat are properties that can be used to precisely place the exact condition of a substance. A minimum of two of these properties are required to pinpoint the state of any substance.

Properties are classified as Extensive & Intensive properties if a physical property of a system which does not depend on the system size or the amount of material in the system is known as Intensive properties. Extensive properties, on the other hand, are those that are dependent on the system size or the amount of material in the system.

Q3) Write about Exact & inexact differentials.

A3)

Exact differentials:

Path functions are properties that are expressed at a specific state of the system and are not at all dependent on the path taken by the system. Examples include pressure, temperature, volume, and so on.

Exact differentials are the derivatives of some other functions as the name suggests.

These are used to express change in point functions. Examples are pressure change dP, volume change dV, etc.

Inexact differentials:

Path functions are properties that depend on the path taken by the system rather than the state of the system. Work heat inexact differentials are useful for expressing very small quantities in these path functions.

Q4) Explain in brief Work.

A4)

Work is one of the most fundamental ways of energy transmission. Work is defined in mechanics as the action of a force on a moving body. A force is a method of transferring an effect from one body to another. A force, on the other hand, never generates a physical impact unless it relates to motion, and hence it is not a form of energy. A simple effect, such as lifting a weight over a short distance, can be achieved by applying a little force over a long distance or a strong force over a short distance.

To have the same impact, the product of force and distance is the same. Work in mechanics is defined as

“The work is done by a force as it acts upon a body moving in the direction of the force.”

Mechanical work refers to the action of a force over a distance (or of a torque over an angle) since other forms of work can be discovered, as mentioned later. The magnitude of mechanical work is the product of the force and the distance travelled parallel to the force.

Work transfer is seen as occurring between the system and its environment in thermodynamics. A system is considered to accomplish work if the only influence on items outside of the system can be reduced to the rising of a weight. The weight may not really be raised, but the total effect on the system would be a weight increase.

Example:

Consider a system with a battery and a motor. A fan is being driven by the engine. The system is at work on the environment. When the fan is replaced with a pulley and a weight, as illustrated, the weight may be lifted using the motor-driven pulley. The only effect on items outside the system is then the lifting of a weight.

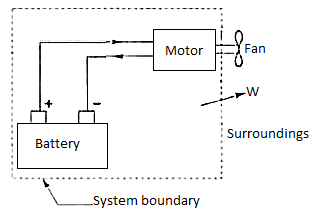
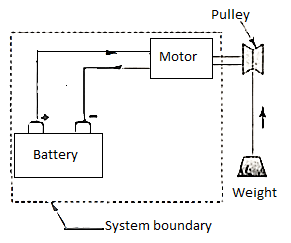
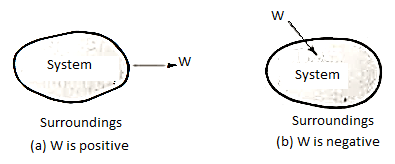
When work is performed by a system, it is arbitrarily assumed to be positive, whereas work performed on a system is assumed to be negative. Work transfer is denoted by the sign W.

The unit of work is N.m or Joule [I Nm= I Joule]. The rate at which work is

Done by, or upon, the system is known as power. The unit of power is J/s or watt.

Work is one of the ways a system and its environment may interact with one another. There are different forms of work transfers that might occur between them.

Q5) Explain quasistatic process.

A5)

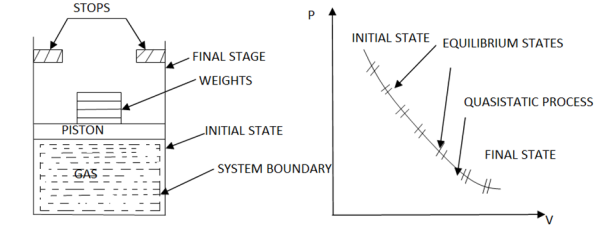
When a process is carried out infinity slowly, it is referred to as a quasistatic process.

When a process proceeds in such a way that the system always remains infinitesimally close to an equilibrium state: quasi-static or quasi-equilibrium process the process proceeds slowly enough to allow the system to adjust itself internally so that properties in one part of the system do not change any faster than those in other parts of the system.

It is a thermodynamic process that occurs at an infinitesimal rate. Every state that the quasi-static process passes through tends to equilibrium. The terms quasi and static refer to thermodynamic properties that remain constant over time. A reversible process is a quasistatic process.

Infinite slowness is characteristic feature of quasi static process.

If the gradient is present in system properties, then the process cannot be quasi static for a finite time. However, if the process's time is infinite, the process can be quasi-static, even if there is some gradient.

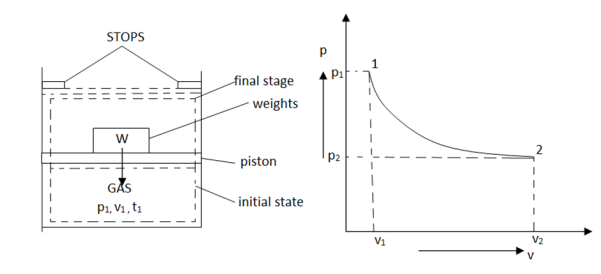
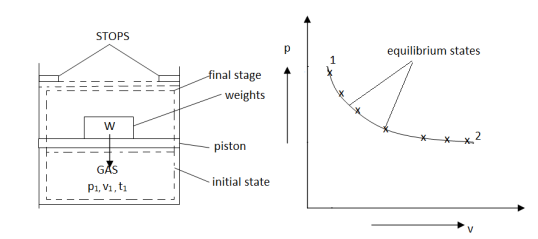
As in figure the piston cylinder assembly is shown and the gas is in equilibrium by the constant pressure (weight) applied on piston and its state can be represented by thermodynamic properties p1, v1, t1.

If the weights are suddenly removed, then the gas will force the piston upwards until the stops or another equilibrium state.

The final equilibrium state can be represented by thermodynamic properties p2, v2, t2.

Now the in between states are not in equilibrium as the spontaneous process occurs. If the weights are now divided into infinite parts and it is taken out one by one so that the process moves on through the successive equilibrium states.

This is a quasi-static process example.

Q6) Define Work & Derive the expression of Work Done.

A6)

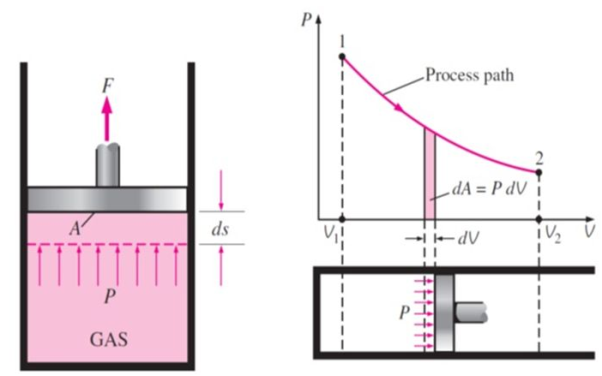
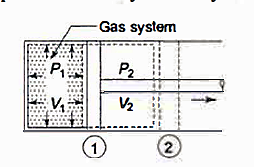
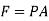
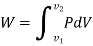
This PdV can be performed only on a quasi-static path.

Work done is measured in Joule (J) or Newton meter (Nm). Rate at which work is done is called as power (Joule/second) or Watt.

Work (w): In thermodynamics, work (w) is the energy transferred by a system to its surroundings. Kinetic energy, potential energy, and internal energy are all types of energy that exist as system properties. Work is a type of energy, but it is energy in motion. A system does not contain work; work is a process performed by or on a system. In general, work in mechanical systems is defined as the action of a force on an object over a distance.

Work performed by a system on its surroundings is regarded as positive, whereas work performed on the system by its surroundings is regarded as negative.

We know that

Work = force x displacement

But in case of thermodynamics works we take force is the product of a pressure p at the boundary and the area A of the moving boundary therefore

DW = pAdl

Where dW is the work done during an infinite displacement dl of the boundary

Since Adl = dv = change in volume

DW = pdv

The conditions under which the above expression is valid are

The system is closed

There are no viscous effects within the system.

The pressure and other properties have the same value on all boundaries of the system

Q7) Show that the cyclic integral of a property is always zero.

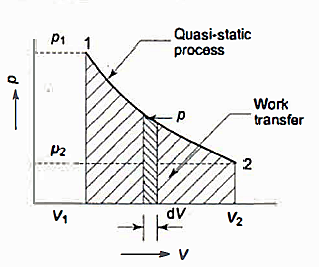
A7)

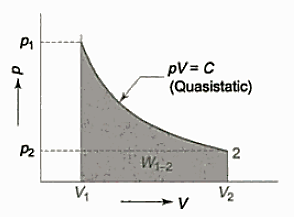
Many quasi-static pathways, such as A, B, or C, can be used to move a system from state 1 to state 2. Because the area under each curve indicates the effort for each process, the amount of work involved in each case is not a function of the process's end states, but rather of the path the system takes to get from state I to state 2. As a result, work is referred to as a path function, and d W is an inexact or imperfect differential.

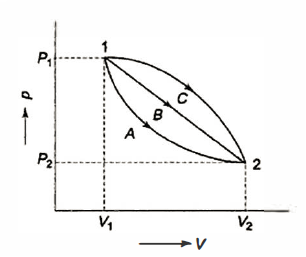
Thermodynamic characteristics are point functions because each attribute has a known value for a particular state. The change in a thermodynamic property of a system during a change of state is independent of the path the system takes throughout the change of state and is determined only by the system's initial and final states. Point function differentials are precise or perfect differentials, and integration is straightforward.

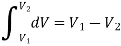
The change in volume thus depends only on the system's end states, regardless of the path the system takes.

Work done in a quasi-static process between two given states, on the other hand, is determined by the path taken.

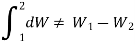
Rather,

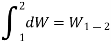
The differential sign is interrupted by a line at its top to distinguish an inexact differential d W from an exact differential dV or dp.

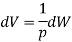
Here,

Here, 1/p is called the integrating factor. Therefore, an inexact differential dW when multiplied by an integrating factor 1/p becomes an exact differential dV.

For a cyclic process, the initial and final states of the system are the same and hence, the change in any property is zero, i.e.

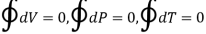
Where the symbol denotes the cyclic integral for the closed path. Therefore,  the cyclic integral of a property is always zero

Q8) Derive the equation for Work for various process in Thermodynamics.

A8)

• Constant Pressure Process (Isobar or Isopiestic Process)

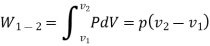
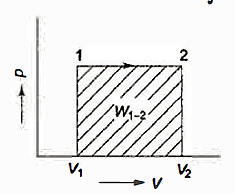
• Constant Volume Process ( Isochoric Process)

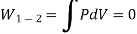
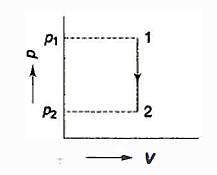
• PV = C

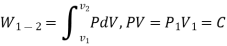
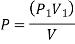
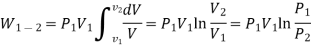
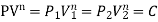
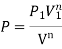
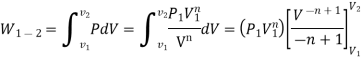
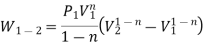
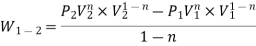
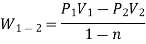
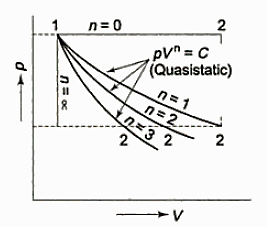
Q9) Explain Electrical, magnetic, gravitational, spring and shaft work

A9)

Electrical Work: The work required to move a unit charge once around the entire circuit is defined as electrical work.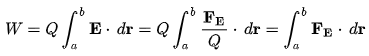

Here, Q = charge on the particle.

E = strength of electric field,

FE = Coulomb force

r = displacement of particle under the action of the Coulomb force.

Magnetic Work:

Magnetic work is the work done by a unit magnetic field in moving a unit charge. It is provided by,

W = F dR

Where, F = force of magnetic field = qv X B

Dr = distance of movement of charge.

Gravitational Work: 

Gravitational work is the work done in moving someone against the force of gravity.

Force due to gravity = F = mg

Gravitational work = F x h = mgh

Where, h = lift of the particle against the force of gravity.

Q10) Explain spring and shaft work

A10)

Spring Work:

When a force is applied to a spring, it will either compress or expand depending on the direction of the force.

This displacement requires some effort from the spring.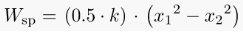

Where, k = stiffness constant of the spring,

x1 = initial distance of the spring from datum

x2 = final distance of the spring from the datum

Shaft Work:

Work is done on a shaft when it is rotated by an external force.

It is given by,

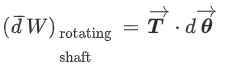
Where, T= torque acting on the shaft

dθ = angular displacement in radians.

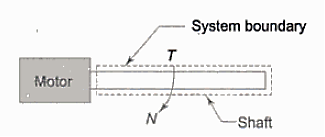
Q11) A 0.78 m3 cylinder is filled with air by opening its valve to the atmosphere and letting it fill up. Work done by air and environment on a system is determined.

A11)

Total work done by the air at atmospheric pressure of 101.325 kPa,

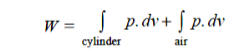
= 0 + p.Δv, it is –ve work as air boundary shall contract

Work done by air = – 101.325 × 0.78 = – 79.03 kJ

Work done by surroundings on system = + 79.03 kJ

Q12) A system consisting of a 5 kg gas is expanded from 1 MPa and 0.5 m3 to 0.5 MPa by means of a squeezing process. p.v1.3 = constant governs the expansion process. U = 1.8pv + 85kJ/kg is the formula for calculating the internal energy of a gas (u). In this case, "u" stands for the specific internal energy, "p" for the pressure, and "v" for the specific volume. Calculate heat and work interaction and internal energy change.

A12)

Given mass of gas, m = 5 kg, pv1.3 = constant

Assuming expansion to be quasi-static, the work may be given as,

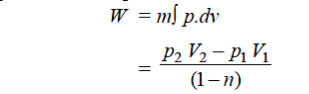
From internal energy relation, change in specific internal energy,

Δu = u2 – u1 = 1.8 (p2v2 – p1v1), kJ/kg

Total change, ΔU = 1.8 × m × (p2v2 – p1v1), kJ

ΔU = 1.8 × (p2V2 – p1V1)

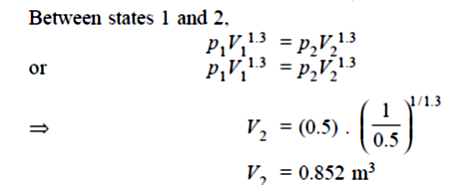
Total change in internal energy, ΔU = –133.2 kJ

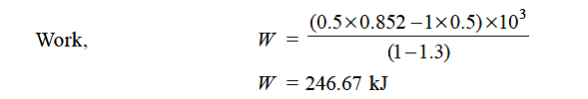
From first law,

ΔQ = ΔU + W

= –133.2 + 246.7

ΔQ = 113.5 kJ

Heat interaction = 113.5 kJ

Work interaction = 246.7 kJ

Change in internal energy = –133.2 kJ

Q13) An ideal gas with molecular weight 16 is compressed from 101.3 kPa at 20°C to 600 KPA using the law pV^1.3 = constant to determine the heat transfer and its direction. Take 1.7 kJ/kg.K as the specific heat at constant pressure of a gas.

A13)

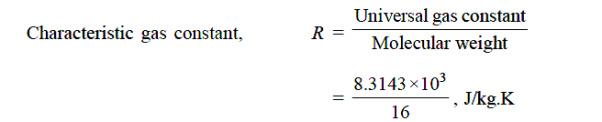
= 519.64, J/kg.K or = 0.51964, kJ/kg.K

R = 0.520, kJ/kg.K

Cv = Cp – R = 1.7 – 0.520

Cv = 1.18, kJ/kg.K

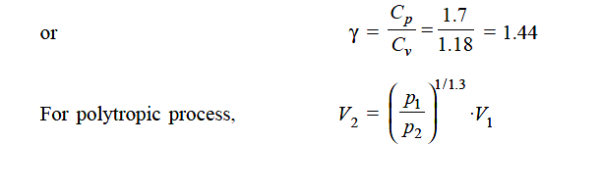
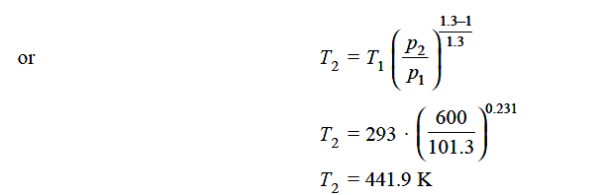
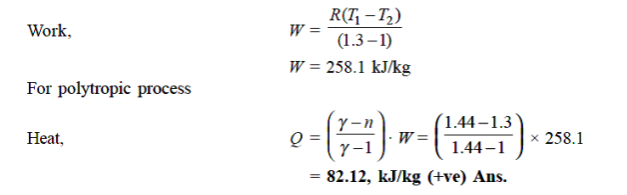
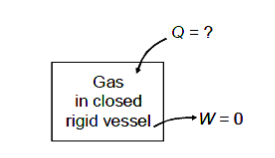
Q14) In a closed, rigid vessel, a gas at 65 kPa and 200°C is heated to 400°C. Assuming the internal energy at 200°C and 400°C is 26.6 and 37.8 kJ/kg, calculate the amount of heat necessary for 0.5 kg of the gas.

A14)

Given m = 0.5 kg

u1 = 26.6 kJ/kg

u2 = 37.8 kJ/kg

As the vessel is rigid therefore work done shall be zero.

W = 0

From first law of thermodynamics.

Q = U2 – U1 + W = m(u2 – u1) + 0

Q = 0.5 (37.8 – 26.6)

Q = 5.6 kJ

Heat required = 5.6 kJ Ans.

Q15) Gas in cylinder is maintained at pressure of 689 kPa. Fluid expands from a volume of 0.04 m3 to 0.045 m3 while pressure remains constant. Paddle wheel in the system does a work of 4.88 kJ on the system. Determine (a) work done by system on the piston (b) the net amount of work done on or by the system.

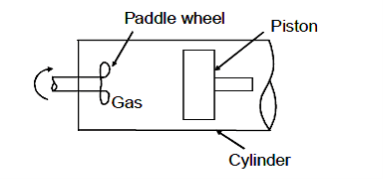
A15)

a)     It is a closed system. If the pressure on face of piston is uniform, then the work done on piston

Can be obtained as,

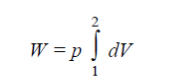
= 689 × 103 (0.045 – 0.04)

W = 3445 J or 3.445 kJ

Work done on piston = 3.445 kJ Ans.

b) Paddle work done on the system = – 4.88 kJ

Net work of system⇒ Wnet = Wpiston + Wpaddle = 3445 – 4880 = –1435 J

Work done on system = 1435 J or 1.435 kJ.

Work done on system = 1.435 kJ Ans

Q16) At 130 kPa and 120°C, a piston–cylinder device contains 0.07 m3 of nitrogen gas. The nitrogen has now been polytropically inflated to a pressure of 100 kPa and a temperature of 100°C. Determine the work done on the boundaries during this process.

A16)

Q17) At 1.0 MPa and 400°C, 0.3 kg of steam is contained in a piston–cylinder apparatus with a set of stops. The stops are positioned to equate to 60% of the starting volume. The steam has now been cooled. If the final state is (a) 1.0 MPa and 250°C, and (b) 500 kPa, calculate the compression work. (c) Determine the temperature in part at the end state (b).

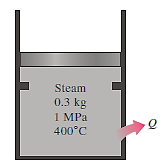
A17)

Q18) At 300 kPa, a quantity of 5 kilogramme saturated water vapour is heated at constant pressure until it reaches 200°C. Calculate the amount of work done by steam in this procedure.

A18)

Q19) 200 L of saturated liquid refrigerant-134a is first contained in a frictionless piston–cylinder system. The piston is free to move and has a mass that allows it to maintain a refrigerant pressure of 900 kPa. The refrigerant will now be heated until it reaches a temperature of 70°C. Calculate the time spent on this task.

A19)