Unit – 2

Temperature

Q1) What do you mean by Temperature?

A1)

A substance's temperature is defined as the degree of hotness or coldness of a body. We know that energy in the universe flows from higher to lower levels. As a result, heat flows from a hotter body to a colder body.

Temperature is not a measure of the quantity of energy in the body; rather, it indicates the level of internal energy in the body.

The absolute temperature is defined as the temperature measured above absolute zero. The capital letter T is used to represent absolute temperatures.

Q2) Explain Thermal Equilibrium & Zeroth law.

A2)

Thermal Equilibrium:

Thermal equilibrium is the absence of heat transfer between two bodies in contact or between a system and its surroundings.

Zeroth Law of Thermodynamics: 

If Body 1 is in thermal equilibrium with Body 3 and Body 2 is in thermal equilibrium with Body 3, it implies that Body 1 is also in thermal equilibrium with Body.

Q3) Explain Different Temperature Scales.

A3)

There are mainly four types of temperature scales.

1. Fahrenheit Scale: It is widely used in the United States. Daniel Gabriel Fahrenheit, a German scientist, founded the company. It is capable of expressing negative temperatures. The following are the key points on this scale:
   1. Freezing point of water: 32° F
   2. Boiling point of water: 212° F
   3. Coldest possible temperature: -459.67° F (absolute zero)

b.     Celsius Scale: The most widely used system and scale in the world. It is also known as the Centigrade scale because it divides the difference between the freezing and boiling points of water into 100 divisions. It is also capable of expressing negative temperatures. The following are the key points on this scale:

1. Freezing point of water: 0° C
2. Boiling point of water: 100° C
3. Coldest possible temperature: -273.15° C (absolute zero)
4. Fahrenheit to Celsius formula Celsius = (Fahrenheit - 32) / 1.8

c.      Kelvin Scale: It is derived from the Celsius scale. It was intended to set the absolute zero temperature to 0 degrees Celsius. The degree scale is not used in this scale. The following are the key points on this scale:

1. Freezing point of water: 273.15 K
2. Boiling point of water: 373.15 K
3. Coldest possible temperature: 0 K (absolute zero)
4. You can convert from Celsius to Kelvin by adding 273.15 to Celsius temperature.

d.     Rankine Scale: It is derived from the Fahrenheit scale. It was intended to set the absolute zero temperature to 0 degrees Celsius. The following are the key points on this scale

1. Freezing point of water: 491.67 R
2. Boiling point of water: 671.67 R
3. Coldest possible temperature: 0 R (absolute zero)
4. You can convert from Fahrenheit to Rankine by adding 459.67 to Fahrenheit temperature.

Q4) Explain 1st Law of thermodynamics for closed system.

A4)

In a system, the transmission of heat and the performance of work may both have the same impact. Heat and work are distinct manifestations of the same thing known as energy, which is conserved. Energy that enters a system as heat may depart as work, or energy that enters as work may leave as heat.

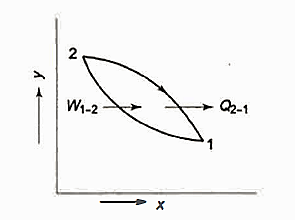
Consider a closed system composed of a known mass of water housed in an adiabatic vessel equipped with a thermometer and a paddle wheel. Allow the paddle wheel to perform a specified amount of work W1 2 on the system. The fall of weight that drives the paddle wheel through a pulley may be used to calculate the amount of work. The system was originally at t1, the same as the atmosphere's temperature, and after work transfer, the temperature was allowed to rise to t2. The pressure is always on me right now. The system's process 1-2 in generalised thermodynamic coordinates X,Y. Allow the insulation to be removed immediately.

The system and its surroundings interact through heat transfer until the system returns to its initial temperature t1, achieving thermal equilibrium with the environment. It is possible to estimate the quantity of heat transfer Q21 from the system during this phase, 2-1. As a result, the system performs a cycle that consists of a certain amount of work input W12 to the system followed by a specific quantity of heat Q21 transferred from the system. It has been shown that this W12 is always proportional to the heat Q21, and this proportionality constant is known as the Joule's equivalent or the mechanical equivalent of heat.

This is the first law for a closed system undergoing a cycle. It is accepted as a general law of nature, since no violation of it has ever been demonstrated.

Heat and work are both measured in the derived unit of energy, the Joule, in the S.I. System of units. As a result, the proportionality constant, J, equals unity (J= 1 Nm/J).

The falling weight drove a paddle wheel, which imparted work to the measured mass of water. The rise in water temperature was measured. Joule also utilised mercury as the fluid system, and then a solid system of metal blocks that absorbed work via friction when rubbed together. Other tests involved giving work in the form of an electric current. In each case, he discovered the same ratio (J) between the amount of effort and the amount of heat that would result in the same consequences in the system.

Prior to Joule, heat was an invisible fluid flowing from a body of higher calorie to a body of lower calorie, and this was known as the caloric theory of heat. It was Joule who first established that heat is a form of energy, and thus laid the foundation of the first law of thermodynamics.

Prior to Joule, heat was thought to be an invisible fluid travelling from a higher calorie body to a lower calorie body, and this was known as the caloric theory of heat. Joule was the first to prove that heat is a type of energy, laying the groundwork for the fundamental law of thermodynamics.

Q5) Explain the concept of total energy.

A5)

The total energy content of a system is the sum of Kinetic energy, Potential energy and the internal energy contained in the system.

E = KE + PE + IE

E = ½ mv2 + mgh + U

In most of the systems, KE and PE are negligible as compared to Internal Energy of the system which is due to vibrational motion of the atoms.

Hence, in general, E = U

Then  Q = U + W 

In differential form, dQ = dU + dW

In integral form,    

The following equation applies exclusively to systems that are in a cycle, and the algebraic total of all energy transfer across system borders is zero. However, if a system undergoes a state transition that involves both heat transfer and work transfer, the net energy transfer will be retained or accumulated inside the system. The net energy transfer (Q- W) will be stored in the system if Q is the amount of heat delivered to the system and W is the amount of work transferred from the system throughout the operation. Because energy in storage is neither heat nor work, it is referred to as internal energy or simply the energy of the system.

As a result, energy is saved during operation. The first law is a specific version of the concept of energy conservation. An equation can also be thought of as a definition of energy. This definition does not provide an absolute value of energy E, but rather the process's change in energy . It can, however, be demonstrated that energy has a fixed value at every state of a system and is therefore a system characteristic.

Q6) Prove that energy (E)is a property.

A6)

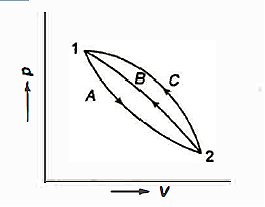
Consider a system that moves from state 1 to state 2 by following path A and then returns to state 1 by following path B.

So, the system undergoes a cycle. Writing the first law for path A

Writing the first law for path B

So,

Similarly, had the system returned from state 2 to state I by following the path C instead of path B.

So,

As a result, the change in energy between two states of a system is the same regardless of the path the system takes in enduring that change of state. If an arbitrary amount of energy is assigned to state 2, the amount of energy in state 1 remains constant regardless of the direction the system takes. As a result, energy has a fixed value for each state of the system. As a result, it is a point function and a system property.

Q7) Write about Macroscopic & Microscopic approach.

A7)

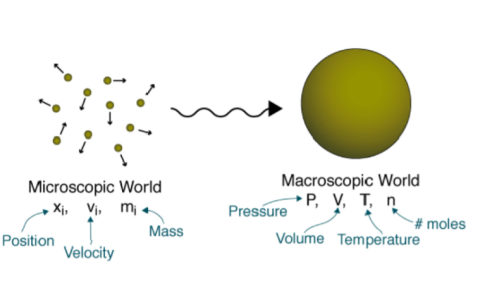
There are two points of view from which the behavior of matter can be studied: the macroscopic and the microscopic.

• Macroscopic

The macroscopic approach considers a limited number of matters while ignoring events occurring at the molecular level. Macroscopic thermodynamics is only concerned with the effect of many molecules acting together, and these effects are perceptible to human senses. For example, the macroscopic quantity, pressure, is the average rate of change of momentum due to all the molecular collision made on a unit area. The effect of pressure can be felt. The macroscopic point of view is not concerned with the action of individual molecule, and the force on a given unit area can be measured by using e.g., a pressure gauge. These macroscopic observations are completely independent of assumptions regarding the nature of matter. All the results of classical or macroscopic thermodynamics can, however, be derived from the microscopic and statistical study of matter.

• Microscopic

From the microscopic point of view matter is composed of myriads of molecules. If it is a gas, each molecule at a given instant has a certain position, velocity, and energy, and for each molecule these changes very frequently because of collisions. In microscopic or statistical thermodynamics, the behavior of a gas is described by summarizing the behavior of each molecule.

Q8) Write about various forms of energy.

A8)

The symbol E refers to the total energy stored in a system. Basically, there are two modes in which energy may be stored in a system:

( a) Macroscopic energy mode

(b) Microscopic energy mode

The macroscopic energy mode includes the macroscopic kinetic energy and potential energy of a system.

Macroscopic Kinetic Energy

Lf the elevation of the fluid element from an arbitrary datum is z, then the

Macroscopic potential energy Ep by virtue of its position is given by

The microscopic energy mode refers to the energy contained in the system's molecule and atomic structure, which is known as molecular internal energy or simply internal energy and is commonly represented by the symbol U. Molecules are the building blocks of matter. Molecules are in random thermal motion (for a gas) with an average velocity, interacting with one another and with the walls all the time.

The molecules may be rotated and vibrated as a result of a collision. Translational kinetic energy, rotational kinetic energy, vibrational energy, electrical energy, chemical energy, and nuclear energy are all possible.

Lf N is the total number of molecules in the system, then the total internal

Energy,

In an ideal gas there are no intermolecular forces of attraction and repulsion, and the internal energy depends only on temperature. Thus

Magnetic energy, electrical energy, and surface (tension) energy are further types of energy that a system might contain. In the absence of these forms, a system's total energy E is given by

Q9) Explain the term internal energy.

A9)

Internal Energy:

The energy contained within a thermodynamic system is referred to as its internal energy. It is the amount of energy required to develop or prepare a system in any given internal condition. It excludes the kinetic energy of motion of the system as a whole, as well as the potential energy of the system as a whole owing to external force fields, which includes the energy of displacement of the system's surroundings. It maintains track of the system's energy gains and losses as a result of changes in its internal condition. Internal energy is quantified as a deviation from a conventional state-defined reference zero.

The difference is determined by thermodynamic processes that transport the system between the reference and current states of interest.

Internal energy is a broad attribute that cannot be measured directly. The thermodynamic processes that characterise internal energy include chemical substance transfers or energy transfers as heat, as well as thermodynamic work. Changes in the system's several variables, such as entropy, volume, and chemical composition, are used to measure these processes. It is not always required to consider all of the system's intrinsic energies, such as the static rest mass energy of its component materials.

The system is said to be closed when mass transfer is prevented by impermeable containing walls, and the first law of thermodynamics defines the change in internal energy as the difference between the energy added to the system as heat and the thermodynamic work done by the system on its surroundings. If neither substance nor energy passes through the confining walls, the system is said to be isolated, and its internal energy cannot change.

Q10) Explain the term Enthalpy in brief.

A10)

Enthalpy:

• One of the fundamental quantities which occurs in thermodynamics is the sum of internal energy (u) and pressure volume product (pv). This sum is called Enthalpy (h).
• 
• The enthalpy of a fluid is the property of the fluid since it consists of the sum of a property and the product of the two properties.
• Since enthalpy is a property like internal energy, pressure, specific volume and temperature, it can be introduced into any problem whether the process is a flow or a non-flow process.

At constant pressure
where is the specific enthalpy, a property of the system.
Heat transferred at constant pressure increases the enthalpy of a system.
For an ideal gas, the enthalpy becomes

Since the internal energy of an ideal gas depends only on the temperature (Eq. 4.11), the enthalpy of an ideal gas also depends on the temperature only, i.e.

Total enthalpy
Also

Q11) At 130 kPa and 120°C, a piston–cylinder device carries 0.25 kg of nitrogen gas. The nitrogen is now expanded to a pressure of 100 kPa isothermally. Determine the work done on the boundaries during this process.

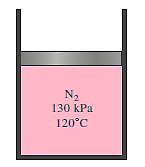
A11)

Q12) At first, a piston–cylinder apparatus contains 0.15 kg of air at a pressure of 2 MPa and a temperature of 350°C. The air is expanded isothermally to 500 kPa, then compressed polytropically to the starting pressure using a polytropic exponent of 1.2, and then compressed at constant pressure to the initial condition. Determine the boundary work for each process as well as the cycle's net-work.

A12)

Q13) Consider a river flowing toward a lake at a rate of 500 m3/s at a height of 90 m above the lake's surface with an average velocity of 3 m/s. Calculate the total mechanical energy of river water per unit mass and the river's overall power generating potential at that place.

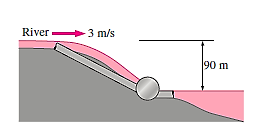
A13)

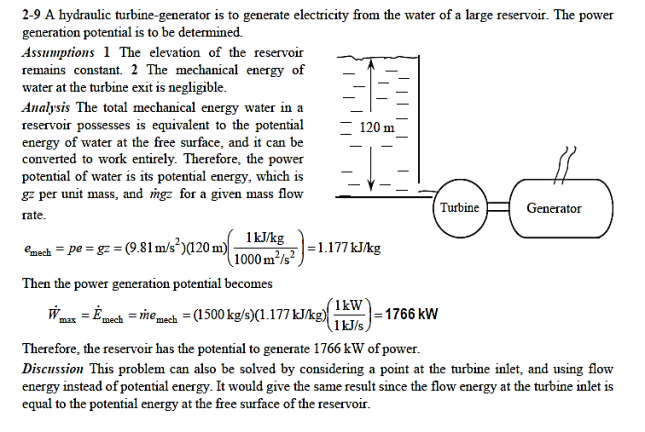
Q14) Installing a hydraulic turbine–generator 120 m below the free surface of a huge water reservoir that can deliver water at a steady rate of 1500 kg/s will create electricity. Determine the potential for electricity generation.

A14)

Q15) The wind is blowing persistently at 10 m/s in one spot. Calculate the mechanical energy of air per unit mass and the power generation potential of a 60-m-diameter wind turbine at that location. Assume a density of 1.25 kg/m3 for the air.

A15)

Q16) Water is contained in a vertical piston–cylinder arrangement that is heated on top of a range. During the process, 65 Btu of heat is delivered to the water, and 8 Btu of heat is lost via the side walls. Evaporation causes the piston to raise, and the vapour performs 5 Btu of labour. Calculate the change in water energy throughout this process.

A16)

Q17) Window air-conditioning units with a cooling capacity of 5 kW will be used to chill a classroom with a regular capacity of 40 people. At rest, a human should dissipate heat at a rate of roughly 360 kJ/h. Each of the ten lightbulbs in the room has a 100 W rating. The rate of heat transfer to the classroom is predicted to be 15,000 kJ/h through the walls and windows. Determine the number of window air-conditioning units required to keep the room air at a constant temperature of 21°C.

A17)

Q18) Consider a room that is initially 20 degrees Celsius outside. A 100-W lamp, a 110-W TV, a 200-W refrigerator, and a 1000-W iron are all in the room. Determine the rate of growth in the energy content of the room when all of these electric gadgets are turned on, assuming no heat transfer through the walls.

A18)

Q19) A house is expected to lose 60,000 Btu/h of heat during winter design circumstances. Internal heat gain is predicted to be 6000 Btu/h due to humans, lighting, and appliances. Determine the required rated power of these heaters in kW to keep the house at a constant temperature if it will be heated by electric resistance heaters.

A19)

Q20) (a) An iron that has been left plugged in heats a room. Is this a matter of heat or of work? Assume the entire room is the system, including the iron.

(b) When a gas is compressed in a piston–cylinder mechanism, its temperature rises. Is this a matter of heat or of work?

(c) Candles are used to heat an insulated room. Is this a matter of heat or of work? Assume the entire room is the system, including the candles.

A20)

(a)  It is a work interaction since the electrons are crossing the system boundary, thus doing electrical work.

(b) It is a work interaction.

(c)  This is neither a heat nor a work interaction since no energy is crossing the system boundary. This is simply the conversion of one form of internal energy (chemical energy) to another form (sensible energy).