Unit - 3

Definition of pure substance

Q1) Explain Pure substance in brief.

A1)

Pure substance

A pure substance is one that has a consistent chemical composition throughout. Examples include water, helium, carbon dioxide, and nitrogen. It does not have to be a single chemical element if it is uniform throughout, such as air. A mixture of phases of two or more substances, such as ice and water (solid and liquid) or water and steam, can still be a pure substance if it is homogeneous (liquid and gas).

Phases & Properties of a pure substance

There are three basic phases: solid, liquid, and gas, but a substance can have multiple phases within the basic phase. Solid carbon (diamond and graphite) and iron (three solid phases) are two examples. Nonetheless, thermodynamics only deals with the primary phases.

•         Solids have the strongest molecular bonds

•         Solids are densely packed three-dimensional crystals.

•         Their molecules do not move relative to one another.

•         The molecular spacing of liquids is comparable to that of solids, but their molecules can float in groups.

•         Within the groups, there is molecular order.

•         Molecular bond strength is the weakest.

•         Molecules in the gas phases are dispersed and lack an ordered structure.

•         The molecules move erratically and collide with one another.

•         Because their molecules have a higher energy level, they must release a lot of energy to condense or freeze.

Q2) What do you mean by Ideal Gas?

A2)

An ideal gas is a theoretical gas made up of a collection of randomly moving point particles that only interact via elastic collisions. The ideal gas concept is useful because it obeys the ideal gas law, which is a simplified equation of state, and is amenable to statistical mechanics analysis.

Most real gases behave qualitatively like ideal gases under normal ambient conditions such as standard temperature and pressure. In general, deviation from an ideal gas tends to decrease with higher temperature and lower density, as the work performed by intermolecular forces becomes less significant when compared to the kinetic energy of the particles, and the size of the molecules becomes less significant when compared to the size of the molecules.

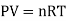
An ideal gas follows this equation.

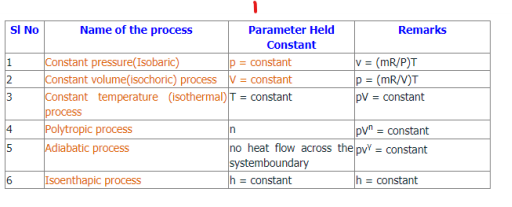
Equation Table for an Ideal Gas

Q3) What do you mean by Real Gas?

A3)

Real gas effects, as opposed to Perfect or Ideal Gas effects, refer to an assumption base that takes the following into account:

•Compressibility effects

•Variable heat capacity

•Van der Waals forces

•Non-equilibrium thermodynamic effects

•Issues with molecular dissociation and elementary reactions with variable composition.

For most applications, such a thorough examination is "overkill," and the ideal gas approximation is used. Real-gas models must be used near the condensation point of gases, near the critical point, at extremely high pressures, and in a variety of other unusual situations.

The term "real gas" usually refers to a gas that does not act as an ideal gas. The behavior of gaseous molecules can be explained by their interactions. Such intermolecular interactions between gas particles explain why the ideal gas law does not apply to actual gases. A real gas may thus be defined as a non-ideal gas containing molecules that occupy a certain amount of space and can interact with one another.

The Dutch scientist Johannes van der Waals amended the ideal gas law to describe the behavior of actual gases by explicitly incorporating the effects of molecule size and intermolecular interactions. The actual gas equation of Van der Waal is provided here.

Real gas law equation,

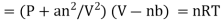
Where a and b represent the empirical constant which is unique for each gas.

represents the concentration of gas.

P represents pressure

R represents a universal gas constant and T is the temperature

Q4) Explain Law of corresponding states.

A4)

In a homogeneous mixture of inert gases, having temperature T, Pressure P, Volume V. Where n = number of moles

Then,

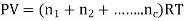
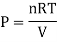
So, P1 + P2+ P3+………+Pc = P

In certain gases, the compressibility factor Z is a function of P & T. On the coordinates of P & Z when the plot of constant Temp is made.

From this plot P & Z can be found out, on the other hand V is calculated from
 

For each substance there is a compressibility factor chart. The shapes of vapor dome and of the constant temperature lines on the P-V planes are similar for all substances. But remember scales are different. This is exploited by using dimensionless properties also known as reduced properties.

,

r = reduced state & c = Critical state

The relation between this reduced state is known as Law of corresponding states.

Q5) Explain the transformation of ice to water and water to steam.

A5)

The transformation of ice to water and water to steam is referred to as phase transformation. It takes place at a constant temperature and a constant pressure.

• Sub-cooled ice:

Sub-cooled ice is ice that has a temperature lower than its freezing point of 0°C. As a result, ice at -6°C, -13°C, and -29°C will be sub-cooled ice. As a result, ice at -6°C will have 6 degrees of sub-cooling.

• Super-heated steam:

Superheated steam is steam that has a temperature higher than its boiling point at a given pressure. Superheated steam has a temperature of 112 degrees Celsius and a pressure of one atmosphere.

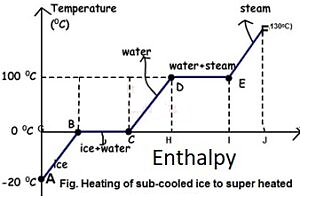
Figure: Phase Transformation of water

From A to F, subcooled ice is heated to superheated steam.

• Process A-B

Sensible heating of sub-cooled ice from -20 to 0 degrees Celsius. Ice is -20 degrees Celsius at point A and 0 degrees Celsius at point B, but there is no phase change.

• Sub cooled liquid

A sub-cooled solid is any substance that is at a temperature lower than its freezing point. Sensible heat gained during the AB process.

• Process B-C

At 0 degrees Celsius, ice melts. It only involves latent heat.

• Dry solid

A saturated solid is a solid that is at its freezing temperature and pressure. Ice at 0°C is a dry solid at point B.

• Wet solid

A Wet Solid is any solid that is frozen and liquid at the same time. As a result, the transition from point B to point C is a phase change process. Remember that a phase change process always occurs at constant temperature and pressure. As a result, it is both an isothermal and an isobaric process. Process C-D

Water can be heated safely from 0°C to 100°C.

• Sub cooled liquid

A sub-cooled liquid is any liquid that has a temperature lower than its boiling point at a given pressure.

Example: water at 13C or below 100C at 1atm pressure will be sub-cooled water. Water at 112C at 2atm will also be sub-cooled water because boiling point at 2 atm is.

• Saturated liquid

Any liquid that has reached its boiling point at a given pressure is said to be saturated. Water, for example, has a boiling point of 120 degrees Celsius at 2 atmospheres of pressure. As a result, water at 120 degrees Celsius and 2 atmospheres of pressure is saturated water.

• Process D-E

Water begins to change into steam vapour at 100C after further heating at point D, and vapour formation is complete at point E at 100C. Temperature and pressure remain constant during phase change. As a result, phase change is both isothermal and isobaric

• Dry Saturated Vapour

Dry saturated vapour is any vapour that has reached its boiling point at a given pressure but contains no liquid. As a result, water vapour at point E at 100 degrees Celsius will be a dry saturated vapour. There should be no liquid present alongside the vapour.

• Process E-F

Further heating at constant pressure raises the temperature of the steam to, say, 130 degrees Celsius. Superheated steam is 130 degrees Celsius at 1 atmosphere pressure.

• Super-heated vapour

Superheated vapour is vapour that has a temperature higher than its boiling temperature at a certain pressure.

• Degree of superheat

The difference between a vapor's actual temperature and its boiling temperature at a given pressure. Thus, at 1 atm pressure, the degree of super heat is 30 when vapour is at 130C, and at 2 atm pressure, when vapour is at 139C, the degree of super heat is 19 (139-120=19).

Q6) Explain Phase Equilibrium diagram on P-T coordinates

A6)

Phase Equilibrium diagram on P-T coordinates

Heating of ice at 0 C to steam at 250 C at constant pressure of 1 atm is considered.

• 1-2 Solid (Ice) = Heating
• 2-3 melting of ice at 0 C
• 3-4 is liquid heating
• 4-5 is vaporization of water at 100 C
• 5-6 is vapour state
• Process will be reversed from 6 -1 upon cooling
• Fusion curve passes through point 2,3
• Vaporization curve passes through 4,5 (indicating Vaporization or condensation at diff temperature and pressure)
• Sublimation curve is obtained if vapour pressure of solid is measured at diff temp.
• Fusion, Sublimation, Vaporization curve meet at triple point.
• Slope of Sublimation, Vaporization for all substance is + ve
• Slope of Fusion curve for most is + Ve, but for Water is – Ve.
• Liquid boiling temp is very sensitive to pressure, which is indicated by Vaporization curve, which gives saturation temperature at diff Pressure.

Temp at which a solid melt is not much sensitive to Pressure as indicated by slope of fusion curve

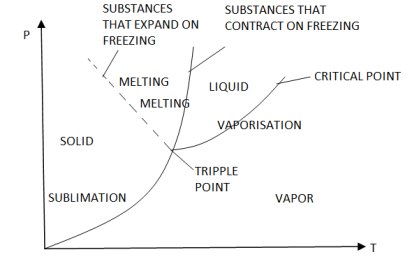
Q7) Write about P-V Diagram.

A7)

If we consider the pressure-cylinder device, but with some weights above the piston, removing the weights one at a time to decrease the pressure and allowing heat transfer to obtain an isothermal process, we will obtain one of the P-v diagram curves.

P-V Diagram

The solid phase, solid liquid, and solid-vapor saturation regions can be added to the P-v diagram. Because some substances, such as water, expand when they freeze, while the rest (the majority) contract during the freezing process, the P-v diagram with solid phase has two configurations.

P-v diagram for a substance that contracts during freezing (left) and for a substance that expends during freezing (right).

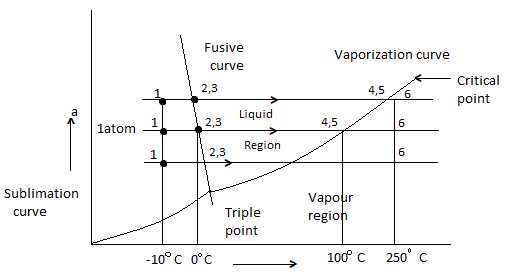
Q8) What do you mean by the term triple point?

A8)

Triple point

In thermodynamics, a substance's triple point is the temperature and pressure at which its three phases (gas, liquid, and solid) coexist in thermodynamic equilibrium. It is the temperature and pressure at which the sublimation, fusion, and vaporisation curves intersect.

Phase Diagram (P-T) & Triple Point

Phase Diagram (P-T) & Triple Point

The P-T diagram is often called the phase diagram since all three phases are separated by three lines.

• Solid - vapor sublimation
• Solid - liquid melting
• Liquid - vapor vaporization

Q9) What do you mean by the term Critical point?

A9)

In physics, a critical point is a set of conditions under which a liquid and its vapour become identical. The critical temperature, critical pressure, and critical density are the conditions that define the critical point for each substance.

Example: The critical conditions can be met by filling a closed vessel with a pure substance that is partly liquid and partly vapour, so that the average density equals the critical density. The vapour pressure rises as the temperature rises, and the gas phase becomes denser. The liquid expands and becomes less dense until, at the critical point, the densities of the liquid and vapour become equal, eradicating the phase boundary. If the starting average density is too low, all of the liquid will evaporate before the critical temperature is reached. If the initial average density of the liquid is too high, it will expand to fill the container.

Q10) Explain Phase – Change Processes of Pure Substances

A10)

It is critical to consider the liquid to solid phase change process at this point. Not so much solid to liquid because thermodynamics only deals with liquid to gas (or vice versa) conversion to generate energy.

Consider water in a piston-cylinder device at room temperature (20°C) and normal atmospheric pressure (1 atm). Water is in the liquid phase, and it is referred to as compressed liquid or sub cooled liquid (not about to vaporize).

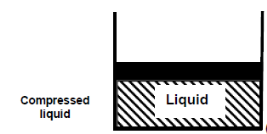
When we add heat to water, its temperature rises until it reaches 50°C. The specific volume v will increase as the temperature rises. As a result, the piston will move slightly upward, maintaining constant pressure (1 atm).

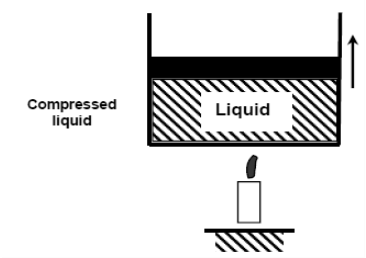
If we continue to add heat to the water, the temperature will rise until it reaches 100°C. Any additional heat will vaporise some water at this point. The point at which water begins to vaporise is referred to as saturated liquid.

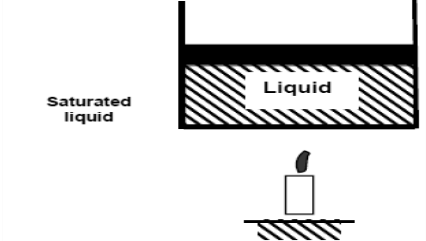
As we continue to heat water, more vapour is produced while the temperature and pressure remain constant (T = 100°C and P = 1 atm). The only property that varies is the volume. These conditions will not change until the last drop of liquid has been vaporised. At this point, the cylinder is filled with vapour at 100°C. This is referred to as saturated vapour.

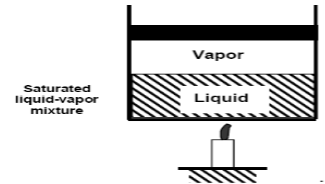
The state where two phases exist between saturated liquid (only liquid) and saturated vapour (only vapour) is known as a saturated liquid-vapor mixture.

Saturated vapour phase on further addition of heat becomes superheated vapor.

Q11) A 0.5-m3 rigid tank initially contains refrigerant-134a at 160 kPa and 40% purity. Until the pressure hits 700 kPa, heat is transmitted to the refrigerant. Calculate (a) the mass of the refrigerant in the tank and (b) the heat transfer rate.

A11)

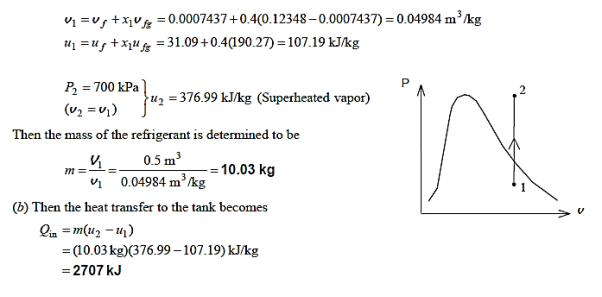
Q12) At 160 psia, a 20-ft3 rigid tank contains saturated refrigerant-134a vapour. The pressure drops to 50 psia as a result of heat transfer from the refrigerant. Determine (a) the end temperature, (b) the amount of refrigerant that has condensed, and (c) the heat transfer by plotting the process on a P-v diagram with saturation lines.

A12)

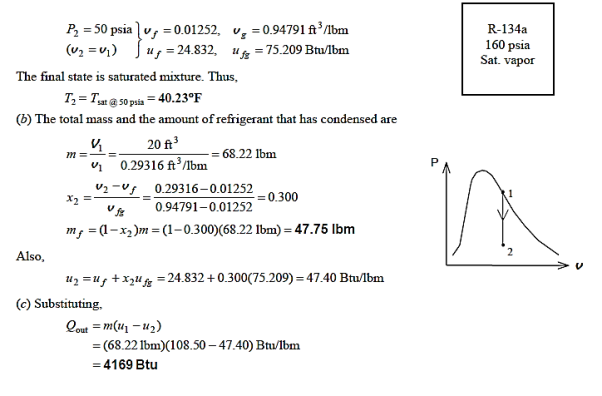
Q13) 5 kg of a saturated liquid–vapor mixture of water at l00 kPa is contained in a well-insulated rigid tank. Three-quarters of the mass is in the liquid phase at first. When the switch is turned on, an electric resistor in the tank is connected to a 110-V source, and a current of 8 A passes through it. Calculate how long it will take to evaporate the whole contents of the tank. Also, draw a T-v diagram with saturation lines to describe the process.

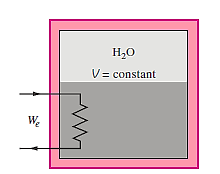
A13)

Q14) A partition divides an insulated tank into two sections. The tank contains 2.5 kg of compressed liquid water at 60°C and 600 kPa in one section and is evacuated in the other. The water expands to fill the entire tank after the divider is removed. For a final pressure of 10 kPa, calculate the final temperature of the water and the capacity of the tank.

A14)

Q15) At 800 kPa and 70°C, a piston–cylinder device stores 5 kg of 134a refrigerant. The refrigerant is now cooled under steady pressure until it reaches 15°C and exists as a liquid. Calculate the quantity of heat lost and depict the process using a T-v diagram with saturation lines.

A15)

Q16) At 120 psia and 2 ft3, a piston–cylinder device contains 0.5 lbm of water. The water now receives 200 Btu of heat while its pressure remains constant. Determine the water's final temperature. Also, draw a T-v diagram of the process with saturation lines.

A16)

Q17) At a constant pressure of 175 kPa, 5 L of saturated liquid water is contained in an insulated piston–cylinder apparatus. A paddle wheel stirs the water for 45 minutes while an 8 A current passes through a resistor in the water. Determine the voltage of the source if half of the liquid evaporates during this constant pressure operation and the paddle-wheel effort is 400 kJ. Also, draw a P-v diagram with saturation lines to describe the process.

A17)

Q18) Steam is originally contained in a piston–cylinder arrangement at 1 MPa, 450°C, and 2.5 m3. Steam is allowed to cool at a constant pressure until it condenses for the first time. Determine (a) the mass of the steam, (b) the ultimate temperature, and (c) the quantity of heat transfer on a T-v diagram regarding saturation lines.

A18)

Q19) At 50 psia and 80°F, a rigid tank holds 20 lbm of air. The air is now heated until it has doubled in pressure. Determine (a) the tank's volume and (b) the heat transfer rate.

A19)

Q20) At 250 kPa and 550 K, hydrogen is contained in a 3-m3 rigid tank. The gas will now be cooled until it reaches a temperature of 350 K. Calculate (a) the tank's final pressure and (b) the quantity of heat transfer.

A20)