Unit - 6

Clausius inequality

Q1) What do you mean by Clausius inequality.

A1)

The integral of dQ / T is always less than or equal to zero.

∮ dQ / T ≤ 0 

This inequality holds true for all cycles in the universe, with no exceptions.

Consider a system connected to a thermal energy reservoir at a constant thermodynamic (i.e., absolute) temperature of TR via a reversible cyclic device to demonstrate the validity of the Clausius inequality.

The cyclic device receives heat ∂QR from the reservoir and supplies heat Q to the system, the temperature at the boundary being T (a variable), while producing work ∂Wrev.

The system produces work ∂Wsys as a result of this heat transfer. 

Balancing the combined system identified by dashed lines yield

ΔWc = δQR - dEc

Considering that the cyclic device is a reversible one, we have

δQR  / TR = δQ / T

Eliminating ∂QR from the two relations above yields

ΔWc = TR δQ / T - dEc

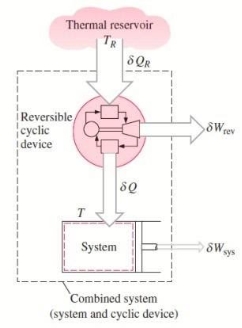
We let the system go through one cycle while the cyclic device goes through an integral number of cycles. The preceding relationship then becomes

Wc = TR ∮ dQ / T

The net work for the combined cycle is represented by ∂WC, which is the cyclic integral of WC.

During a cycle, it appears that the combined system exchanges heat with a single thermal energy reservoir while involving (producing or consuming) work Wc. We reason that Wc cannot be a work output and thus cannot be a positive quantity based on the Kelvin-Planck statement of the second law, which states that no system can produce a net amount of work while operating in a cycle and exchanging heat with a single thermal energy reservoir.

∮ dQ / T ≤ 0

Q2) Explain in brief about Entropy.

A2)

Clausius realized in 1865 that he had discovered a new thermodynamic property and he chose to name this property entropy. It is designated S and is defined as, dS = (dQ / T)

The entropy changes of a system during a process can be determined by integrating above Eq. Between the initial and the final states

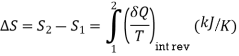
Therefore, the entropy of a substance can be assigned a zero value at some arbitrarily selected reference state, and the entropy values at other states can be determined from above Eq

Entropy is defined as a measure of randomness or disorder of a system.  Aside from the general definition, there are several definitions for this concept. We do not consider the microscopic details of a system from the standpoint of entropy in thermodynamics. Entropy, on the other hand, is used to describe a system's behaviour in terms of thermodynamic properties such as temperature, pressure, entropy, and heat capacity. This thermodynamic description considered the systems' state of equilibrium. Meanwhile, the statistical definition developed later focused on the thermodynamic properties defined in terms of the statistics of a system's molecular motions. The entropy of a molecular system is a measure of its disorder.

Q3) Prove that entropy S is a property

A3)

• Let us consider a system undergoing a reversible process from state 1 to state 2 along path L and then from state 2 to the original state 1 along path M or N.
• Applying the Clausius theorem to this reversible cyclic process

∮ dQ / T = 0

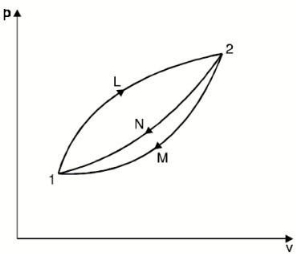
• For cycle 1-L-2-M-1, we have

• For cycle 1-L-2-N-1

• Subtracting equation (2) from equation (1), we have

• As no restriction is imposed on paths L and M, except that they must be reversible, the quantity is a function of the initial and final states of the system and is independent of the path of the process.
• Hence it represents a property of the system.
• This property is known as the “entropy”. 

Q4) What do you mean by Availability:

A4)

Availability is defined as the Max useful work which can be obtained during a process in which the system comes in equilibrium with its surroundings.

Note:

The heat of the system is being exchanged with the environment, it may be both reversible and irreversible.

Useful work is given by,

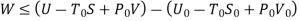
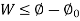
Where, is availability function, i.e., a composite function of both

System and environment.

Thus, the useful work is ≤ the decrease in the availability function.

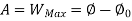
A= Availability

This work is obtained from a decrease in the internal energy of system & heat removed from environment.

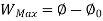
A system has two equilibrium states then,

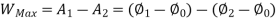
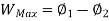
Q5) Derive the equation for Availability in steady flow.

A5)

A mass m is flowing in the system then,

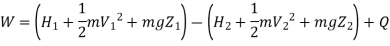
Assuming KE & PE are negligible

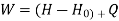
Entropy at entrance & exit = S &

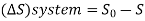
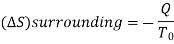
From entropy,

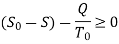
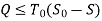
Useful work,

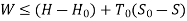
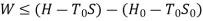
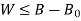
B is called availability function for steady state flow also known as Keenan Function.

The availability & Unavailable quantity are also called Energy & Anergy respectively.

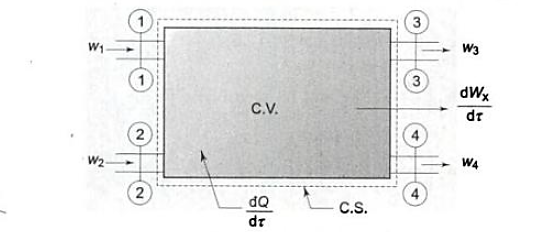
Q6) Derive Mass balance equation for a control volume.

A6)

When a fluid flows through a control volume, its thermodynamic properties can change along space coordinates as well as over time. If the rates of flow of mass and energy through the control surface change over time, so will the mass and energy within the control volume.

The term' steady flow' refers to the constant rates of mass and energy flow across the control surface.

At the steady state of a system, any thermodynamic property has a fixed value at a specific location and does not change over time.

Thermodynamic properties vary along space coordinates but not with time. The term' steady state' refers to a state that is constant or invariant over time.

cross-section of stream,

mass flow rate, kg/s

pressure, absolute N/

specific volume

specific internal energy,

velocity m/s

elevation above an arbitrary datum, m

DQ/dt – net rate of heat transfer through the control surface, J/s

netrate of work transfer through the control surface, J/s

Exclusive of work done at sections 1 and 2 in transferring the fluid through the control surface .

- time, s.

Mass Balance

According to the law of conservation of mass, if no mass accumulates within the control volume, the mass flow rate entering must equal the mass flow rate leaving.

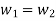
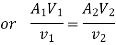
This is referred to as the equation of continuity.

Q7) Write Energy balance equation and explain energy analysis.

A7)

Work transfer in a flow process can be of two types: external work and flow work. The term "external work" refers to all work transfer across the control surface that is not caused by normal fluid forces. Shear (shaft or stirring) work and electrical work are the only types of external work that matter in engineering thermodynamics. Only external work, Wx, takes the form of shaft work. The flow work is the displacement work done by a f              luid of mass dm1 at the inlet section I and a fluid of mass d2 at the exit section 2, which are (-p1 v1dm1) and (+p2v2dmi) respectively. As a result, total work transfer is given by

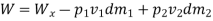
In the rate form,

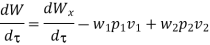
Because there is no energy accumulation, the total rate of flow of all energy streams entering the control volume must equal the total rate of flow of all energy streams leaving the control volume. This can be expressed mathematically as follows.

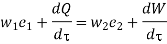
Substituting for from eq 5.4

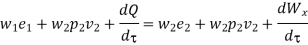
Where e1 and e2 denote the energy carried into or out of the control volume per unit mass of fluid.

The specific energy e is given by

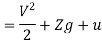
Substituting the expression for e in 5.5

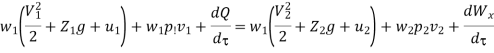
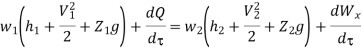
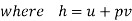
And since let

Dividing by dm/d

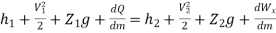
Or it can also be written as

In differential form it is written as

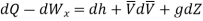
Mass balance

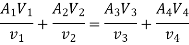
Energy balance

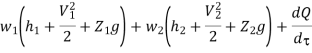
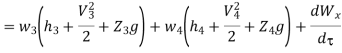
Q8) Water can be cooled to a temperature (say, 10 o C) below its normal freezing point with care. The cold water produced in this manner is commonly referred to as super cooled water. Is the supercooled water in an equilibrium state?

A8)

Consider the Super' cooled water as a system and use the equilibrium criteria to determine whether it is in a state of equilibrium or not. The system has a uniform temperature, so it meets the thermal equilibrium criterion. Because the pressure is uniform throughout the system, the system also meets the mechanical equilibrium criterion. The system contains pure water that is at a constant temperature and pressure.

As a result, the chemical potential is consistent throughout the system. As a result, it also meets the criterion of chemical equilibrium. The system is in thermodynamic equilibrium because it meets the criteria of thermal, mechanical, and chemical equilibrium at the same time. When the system is subjected to a minor disturbance, such as the addition of a small amount of dust or the shaking of the container, the supercooled liquid immediately freezes into ice. As a result, the system is in metastable equilibrium.

Q9) Steam enters a flow device at 1.6 MPa and 300oC with negligible velocity and exits at 0.1 MPa and 150oC with a velocity of 150 m/s. At 15oC, heat interaction with the surroundings occurs only during the flow, and the steam mass flow rate is 2.5 kg/s. Calculate the device's maximum possible output.

A9)

Let us neglect the potential energy change during the flow.

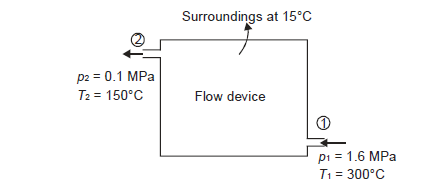
Applying S.F.E.E., neglecting inlet velocity and change in potential energy,

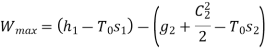
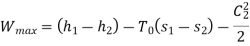
From steam tables

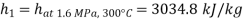
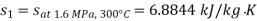
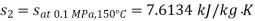
Given 

Maximum possible work=2.5×457.1 kJ/s=1142.75 kW

Maximum possible work=1142.75 Kw

Q10) Two tanks A and B contain 1 kg of air at 1 bar and 50oC, and 3 bar and 50oC when the atmosphere is at 1 bar and 15oC. Determine which tank has the most stored energy. Find out how much air is available in each tank.

A10)

In these tanks the air stored is at same temperature of 50ºC. Therefore, for air behaving as perfect gas the internal energy of air in tanks shall be same as it depends upon temperature alone. But the availability shall be different.

Both the tanks have same internal energy

Availability of air in tank

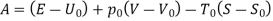
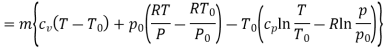
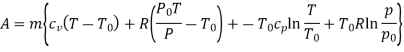
For tank A, , K

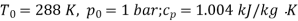
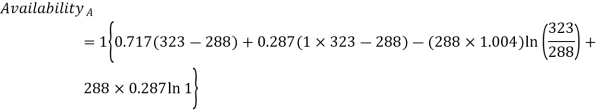
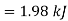
For tank B,

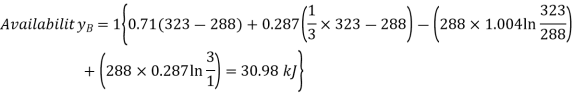
Availability of air in tank B is more than that of tank A

Availability of air in tank A=1.98kJ

Availability of air in tank B=30.98kJ

Q11) At 10 bar, 300oC, 15 kg/s steam enters a perfectly insulated steam turbine and exits at 0.05 bar, 0.95 dry with a velocity of 160 m/s. Assuming a 1 bar atmospheric pressure and a temperature of 15oC. Determine (a) power output, (b) maximum power for given end states, and (c) maximum power obtained from exhaust steam. The turbine rejects heat to a pond with 15oC water.

A11)

From steam tables, Enthalpy at inlet to turbine

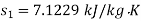
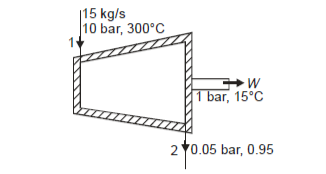
Enthalpy at exit of turbine

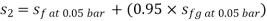
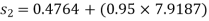
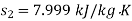
Similarly

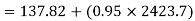
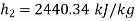
Neglecting the change in potential energy and velocity at inlet to turbine, the steady flow energy equation may be written as to give work output

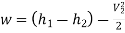
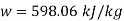
Power output=mw=15×598.06=8970.9 kW

Power output=8970.9 kW

Maximum work for given end states

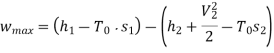
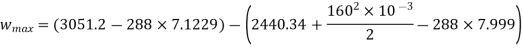
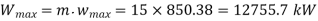
Maximum power output=12755.7 kw

Maximum power that could be obtained from exhaust steam shall depend upon availability with exhaust steam and the dead state. Stream availability of exhaust steam,

Approximately the enthalpy of water at dead state of 1 bar, 15°C can be approximated to saturated liquid at 15°C.

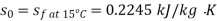
Maximum work available from exhaust steam

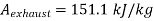
Maximum power that could be obtained from exhaust steam

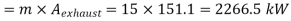
Q12) 5 kg of steam, initially at an elevation of 10 m and a velocity of 25 m/s, goes through some process to arrive at an elevation of 2 m and a velocity of 10 m/s. Determine the availability of the initial and final states. Estimate the change in availability assuming a temperature of 25oC and a pressure of 100 kPa in the environment. Thermodynamic properties u, v, s is as under.

Dead state of water

Initial state

Final state

A12)

Availability at any state can be given by

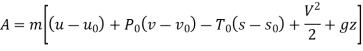
Availability at initial state

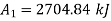
Availability at final state

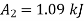
Availability at final stae=1.09 kJ

Change in availability:

Hence availability decreases by 2703.75 kJ

Q13) Exhaust gases from an internal combustion engine leave at 800oC and 1 atmosphere after performing 1050 kJ of work per kg of gas in engine. (Gas Cp = 1.1 kJ/kg K). The temperature outside is 30oC.

• How much available energy per kg of gas is lost by throwing away the exhaust gases?
• What is the ratio of the lost available exhaust gas energy to engine work?

A13)

Loss of available energy=Inversibility =

Here Temperature of surroundings

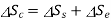
Change in entropy of system

Change in entropy of surroundings=

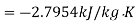
Loss of available energy=303(-2.7954+0.9786)

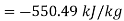
Ratio of lost available exhaust gas energy to engine work

Q14) 10 kg of water is transformed from an initial saturated vapour at 150oC with a velocity of 25 m/s and an elevation of 10 m to a saturated liquid at 20oC with a velocity of 10 m/s and an elevation of 3 m. Determine the availability for the initial state, final state, and change in availability when the environment is 0.1 MPa, 25oC, and g = 9.8 m/s2.

A14)

Let us consider velocities and elevations to be given in reference to environment. Availability is given by

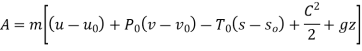
Dead state of water,

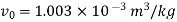
For initial state of saturated vapour at 150℃

For final state of saturated vapour at 20℃

Substituting in the expression for availability

Initial state availability

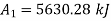
Final state availability

Change in availability, A=

Initial availability =5650.28 kJ

Final availability=2.58 kJ

Change in availability=Decrease by 5647.70 kJ

Q15) A steam turbine has a steady rate of 5 kg/s of steam entering at 5 MPa and 500oC and leaving at 0.2 MPa and 140oC. At 1 atm and 25oC, a heat loss of 600 kJ/s occurs to the environment during flow through the turbine.

Determine

• The availability of steam at inlet to turbine,
• The turbine output
• The maximum possible turbine output, and
• The irreversibility

Neglect the changes in kinetic energy and potential energy during flow.

A15)

Let inlet and exit states of turbine be denoted as 1 and 2

At inlet to turbine

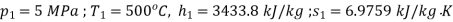
At exit from turbine

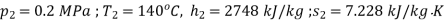
At dead state,

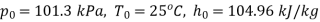
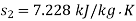
Availability of steam at inlet,

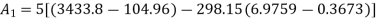
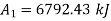
Availability of steam at inlet =6792.43kJ

Applying first law of thermodynamics

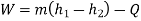
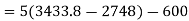
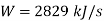
Turbine output =2829 kW

Maximum possible turbine output will be available when irreversibility is zero

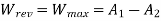
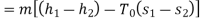
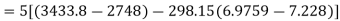
Maximum output =3053.18 kW

Inversibility can be estimated by the difference between the maximum output and turbine output

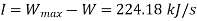
Inversibility=224.18 kW

Q16)500 kJ of heat is removed from an 835 K constant temperature heat reservoir. A system receives heat at a constant temperature of 720 K. The temperature of the surroundings is 280 K, which is the lowest available temperature. Calculate the net loss of available energy due to irreversible heat transfer.

A16)

Here ie surrounding temperature

Availability for heat reservoir

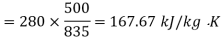
Availability for system

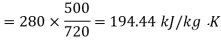
Net loss of available energy=(167.67-194.44)=-26.77 kJ/kg  K

Loss of available energy=26.77 kJ/kg  K

Q17) Describe the operation of an adiabatic steady flow turbine. The enthalpy at the entrance is 4142 kJ/kg and the enthalpy at the exit is 2585 kJ/kg. The flow availability of steam at the entrance and exit are 1787 kJ/kg and 140 kJ/kg, respectively, and the dead state temperature T0 is 300 K. Determine the actual work, the maximum possible work for the given change of state of steam, and the change in entropy of steam per kg of steam. Changes in kinetic and potential energy are ignored.

A17)

Here dead state is given as 300K and the maximum possible work for given change of state of steam can be estimated by the difference of flow availability as given under

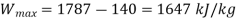
Actual work from turbine,

Actual work=1557 kJ/kg

Actual work=1557 kJ/kg

Maximum possible work-1647 kJ/kg

Q18) A rigid tank holds a 40°C ideal gas, which is agitated by a paddle wheel. On optimal gas, the paddle wheel produces 200 kJ of effort. As a result of heat transmission between the system and the surroundings at 30°C, the temperature of the ideal gas remains constant during this operation. Calculate the ideal gas's entropy change.

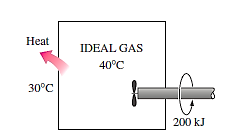
A18)

A rigid tank contains an ideal gas that is being stirred by a paddle wheel. The temperature of the gas remains constant as a result of heat transfer out. The entropy change of the gas is to be determined. Assumptions The gas in the tank is given to be an ideal gas. Analysis The temperature and the specific volume of the gas remain constant during this process. Therefore, the initial and the final states of the gas are the same.

Then s2 = s1 since entropy is a property, therefore S system = 0

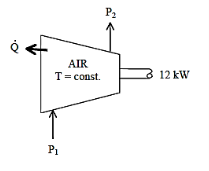
Q19) From P1 to P2, air is compressed by a 12-kW compressor. As a result of heat transmission to the surrounding medium at 10°C, the air temperature remains constant at 25°C throughout the process. Calculate the air's rate of entropy change. List the assumptions you used to solve this problem.

A19)

Air is compressed steadily by a compressor. The air temperature is maintained constant by heat rejection to the surroundings. The rate of entropy change of air is to be determined.

Assumptions 1 This is a steady-flow process since there is no change with time. 2 Kinetic and potential energy changes are negligible. 3 Air is an ideal gas 4. The process involves no internal irreversibilities such as friction and thus it is an iso thermal, internally reversible process.

Properties

Nothing that h=h(T) for ideal gases, we hav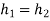e since

Analysis

We take the compressor as the system. Nothing that the enthalpy of air remains constant, the energy balance for this steady-flow system can be expressed in the rate form as

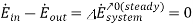
Where is Rate of net energy transfer by heat, work and mass

Rate of change in internal kinetic, potential etc energies

 and

Therefore,

Nothing that the process is assumed to be an isothermal and internally reversible process, the rate of entrooy change of air is determined to be

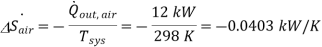
Q20) A Carnot cycle's isothermal heat addition operation adds 900 kJ of heat to the working fluid from a source at 400°C. Calculate (a) the working fluid's entropy change, (b) the source's entropy change, and (c) the total entropy changes for the process.

A20)

Heat is transferred isothermally from a tot the working fluid of a Carnot engine. The entropy change of the working fluid, the change of the source, and the total entropy change during this process are to be determined.

Analysis (a)

This is a reversible isothermal process, and the entropy change such a process is given by

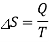
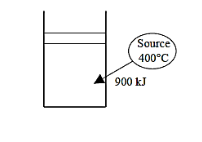
Nothing that heat transferred from the source is equal to the heat transferred to the working fluid and of the source become

(b)

(c) Thus the total entropy change of the process is