Unit - 7

Thermodynamic cycles

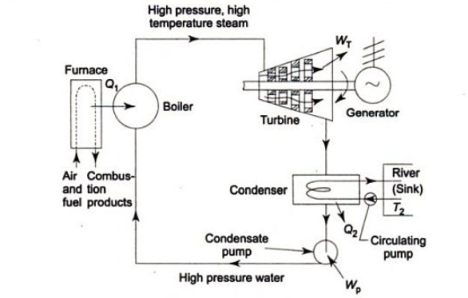
Q1) Explain Rankine Cycle.

A1)

The Rankine cycle is the basic operating cycle of all power plants, in which an operating fluid is continuously evaporated and condensed. The operating fluid chosen is primarily determined by the temperature range available.

• Isobaric heat transfer

The feed pump sends high-pressure liquid into the boiler, which heats it to saturation temperature. The addition of more energy causes the liquid to evaporate until it is completely converted to saturated steam.

• Isentropic expansion

The vapour expands in the turbine, creating work that can be converted to electricity. In practise, the expansion is limited by the cooling medium's temperature and the erosion of the turbine blades caused by liquid entrainment in the vapour stream as the process progresses into the two-phase region. The quality of the exit vapour should be greater than 90%.

• Isobaric heat rejection

The vapor-liquid mixture that exits the turbine is condensed at low pressure, typically in a surface condenser that uses cooling water. The pressure of the vapour in well-designed and maintained condensers is well below atmospheric pressure, approaching the saturation pressure of the operating fluid at the cooling water temperature.

• Isentropic compression

The feed pump raises the pressure of the condensate. Because liquids have a low specific volume, the pump work is relatively small and is frequently overlooked in thermodynamic calculations.

Q2) Write Analysis of Rankine cycle.

A2)

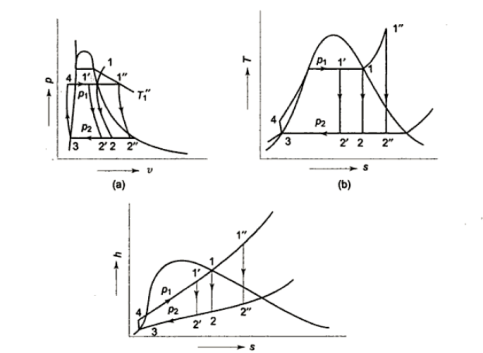
• h4+ Q1 = h1

Q1=h1-h4

• h1= WT+h2

WT = h1 -h2

• h2= Q2 + h3

Q2 =h2-h3

• h3 + Wp = h4

Wp = h4 -h3

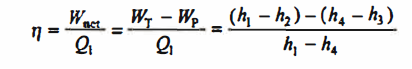
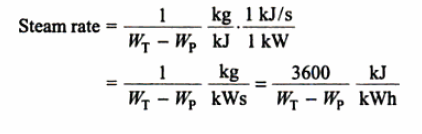
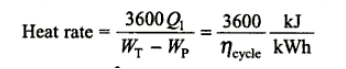
Q3) Explain Brayton Cycle

A3)

The Brayton cycle (also known as the Joule cycle) simulates the operation of a gas turbine engine. The cycle is made up of four stages.

• a - b Adiabatic, quasi-static (or reversible) compression in the inlet and compressor.
• b - c Constant pressure fuel combustion (idealized as constant pressure heat addition);
• c - d Adiabatic, quasi-static (or reversible) expansion in the turbine and exhaust nozzle, with which we

      Take some work out of the air and use it to drive the compressor,

      Take the remaining work out and use it to accelerate fluid for jet propulsion, or to turn a generator for electrical power generation.

• d - a Cool the air at constant pressure back to its initial condition

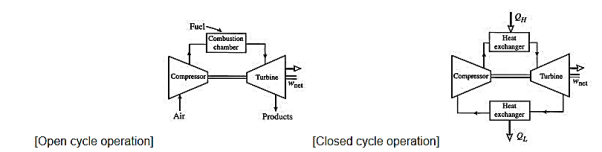
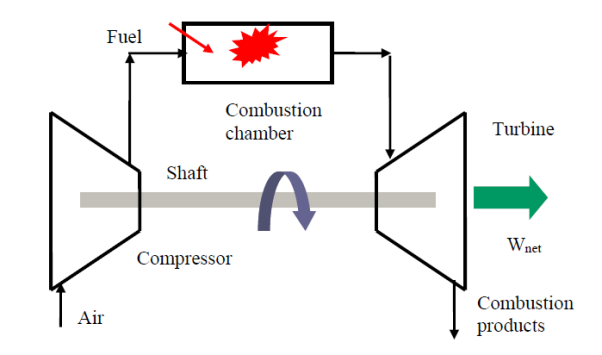
At room temperature, fresh air enters the compressor, where its pressure and temperature are raised.

High-pressure air enters the combustion chamber, where the fuel burns at a constant pressure.

The hot (and high-pressure) gas enters the turbine, where it expands to ambient pressure and generates work.

A gas turbine is a type of engine that is utilised in aircraft propulsion and electric power generation.

      High thermal efficiency of up to 44%.

      Suitable for use in mixed cycles (with steam power plant)

      Great power-to-weight ratio, high dependability, and extended life

      Fast start-up time of roughly 2 minutes, compared to 4 hours for steam-propulsion systems; high back work ratio (ratio of compressor work to turbine work), up to 50%, compared to a few percent in steam power plants.

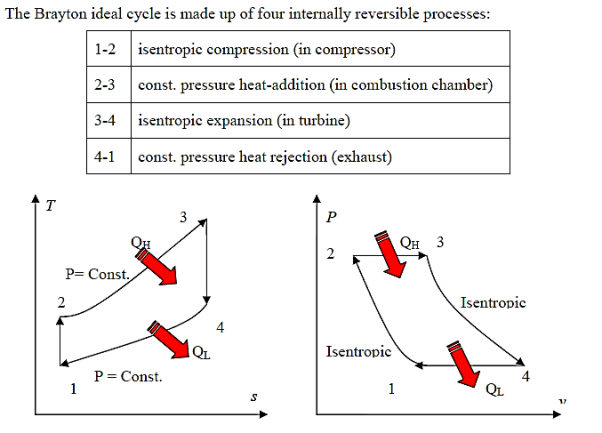
Q4) Write Analysis of  Brayton cycle.

A4)

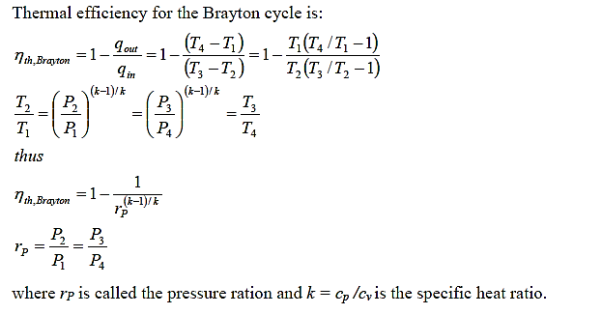
Q5) Explain vapour compression cycle.

A5)

The vapor-compression refrigeration is the most widely used cycle for refrigerators, air-conditioners, and heat pumps.

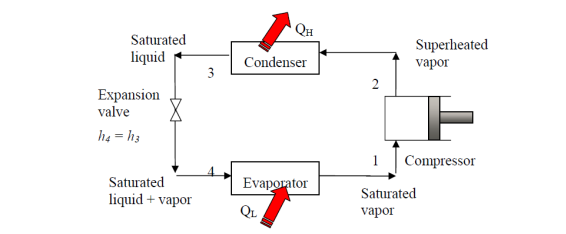
Assumptions for ideal vapor-compression cycle:

•         all irreversibility’s in the evaporator, condenser, and compressor are ignored; and there are no frictional pressure drops.

•         The refrigerant flows through the two heat exchangers at constant pressure (evaporator and condenser)

•         heat losses to the environment are ignored

•         The compression process is isotropic.

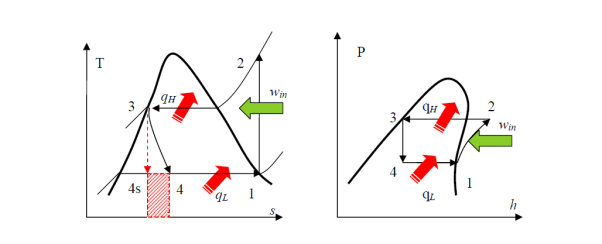
•         A reversible, adiabatic (isentropic) compression of the refrigerant. The saturated vapor at state 1 is superheated to state 2.

Wc =h2 − h1

•         An internally reversible, constant-pressure heat rejection process in which the working substance is de-superheated and then condensed to a saturated liquid at 3. The working substance rejects the majority of its energy to the condenser cooling water during this process.

QH = h2 − h3

•         An irreversible throttling process in which temperature and pressure decrease while maintaining constant enthalpy. At state 4, the refrigerant enters the evaporator as a low-quality saturated mixture.

h3 = h4

•         An internal, reversible, constant-pressure heat interaction in which the refrigerant (two-phase mixture) evaporates to a saturated vapour at state point 1. The refrigerated space surrounding the evaporator provides the latent enthalpy required for evaporation. The refrigeration load is the amount of heat transferred to the working fluid in the evaporator.

QL = h1 − h4

Because throttling is an irreversible process, the ideal compression refrigeration cycle is not an internally reversible cycle.

The refrigerant would enter the evaporator at state 4s if the expansion valve (throttling device) was replaced by an isentropic turbine. As a result, the refrigeration capacity (area under 4-4s) would increase while the net work input would decrease (turbine will produce some work). However, due to the added cost and complexity, replacing the expansion valve with a turbine is not feasible.

The COP increases by 2 to 4% for every °C increase in evaporating temperature or decrease in condensing temperature.

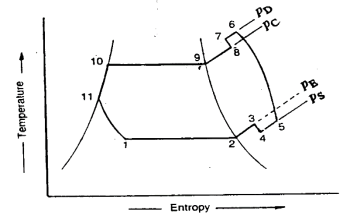
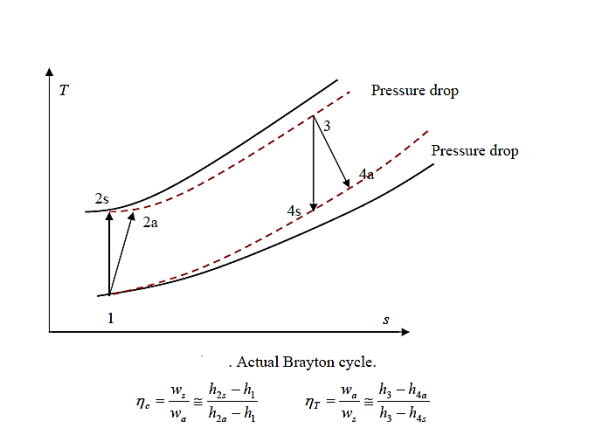
In many ways, the actual vapour compression cycle differs from the theoretical vapour compression cycle, some of which are unavoidable and result in losses. The following are the main differences between the theoretical and actual cycles:

1. The vapour refrigerant that exits the evaporator is superheated.
2. Refrigeration compression is neither isentropic nor polytropic.
3. The condenser sub-cools the liquid refrigerant before it enters the expansion valve.
4. The pressure in the evaporator and condenser drops.

The actual vapour compression cycle on T-s diagram is shown. The various processes are discussed below

The refrigerating effect and compressor work are increased in the first and second cases of superheating the vapour refrigerant. When compared to a saturation cycle at the same suction pressure, the coefficient of performance may be greater, less, or unchanged. Superheating also increases the required displacement of the compressor as well as the load on the compressor and condenser. This is denoted by 2-3 on the T-s diagram.

The temperature of the cylinder walls is somewhere between that of the cold suction vapour refrigerant and that of the hot discharge vapour refrigerant. The heat absorbed by the vapour refrigerant from the cylinder walls during the first part of the compression stroke can be assumed to be equal to the heat rejected by the vapour refrigerant to the cylinder walls. The cooling effect at discharge is similar to the heating effect at suction, as shown in 4-5. At constant pressure, these heating and cooling effects occur. There is a pressure drop due to the frictional resistance of flow, i.e., the actual discharge pressure (Pd) is greater than the condenser pressure (Pc).

This is advantageous because it increases the refrigerating effect per kg of refrigerant flow. It also reduces the volume of refrigerant partially evaporated from liquid refrigerant as it passes through the expansion valve. Large amounts of circulating cooling water at temperatures much lower than condensing temperatures can be used to increase the refrigerating effect.

(d) Process 11-1: Throttling from the condenser pressure to the evaporator pressure represents the expansion of subcooled liquid refrigerant

Effect of Suction Pressure

In the previous article, we discussed how, in practise, the suction pressure (or evaporator pressure) decreases due to the frictional resistance of the refrigerant flow. Consider a hypothetical vapour compression cycle 1'-2'-3-4' in which the suction pressure decreases from ps to ps' as shown on the p-h diagram. It should be noted that the decrease in suction pressure is significant.

1. Decreases the refrigerating effect from (h1 - h4) to (h1'- h4') and
2. Increases the work required for compression from (h2 – h1) to (h2' – h1')

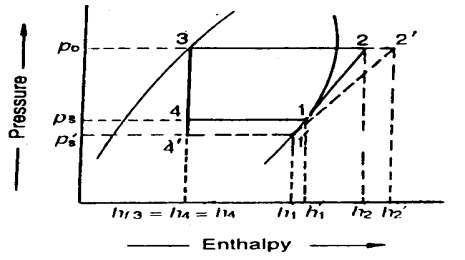
Because the C.O.P. Of the system is the ratio of refrigerating effect to work done, lowering the suction pressure has the net effect of lowering the C.O.P. Of the refrigerating system for the same amount of refrigerant flow. As a result of the decrease in suction pressure, the system's refrigerating capacity decreases, and the refrigeration cost increases.

Effect of Discharge Pressure

We have already discussed how, in practise, the discharge pressure (or condenser pressure) rises due to the frictional resistance of the refrigerant flow. Consider a theoretical vapour compression cycle 1-2'-3'-4' in which the discharge pressure rises from Pd to Pd' as shown on the p-h diagram

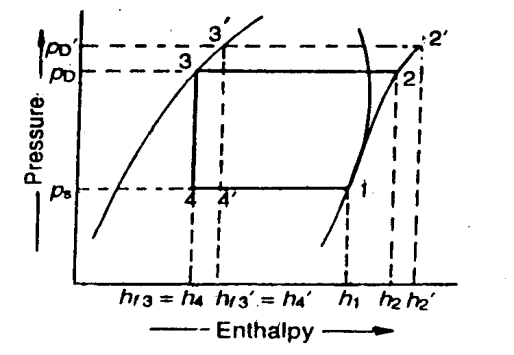
It may be noted that the increase in discharge pressure:

1. Decreases the refrigerating effect from (h1 - h4) to (h1 - h4')
2. Increases the work required for compression from (h2-h1) to (h2' - h1)

From above, we can see that an increase in discharge pressure has the same effect as a decrease in suction pressure. However, an increase in discharge pressure has a less severe effect on the system's refrigerating capacity than a decrease in suction pressure.

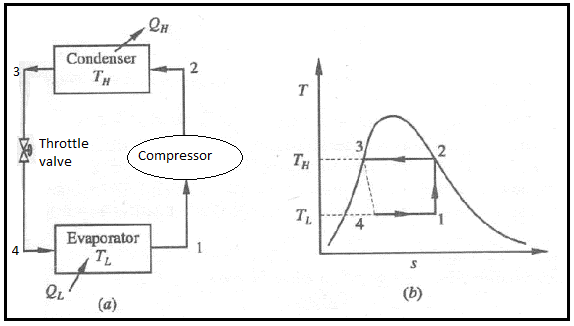
Q6) Analyse Vapour compression refrigeration system.

A6)

Vapour compression refrigeration system analysis:

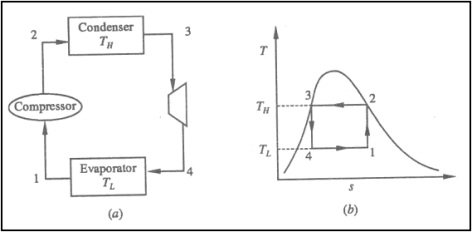
•         1-2: Isentropic compression from state 1 (wet vapour) to state 2 (saturated vapour)

•         2-3: Heat rejection (QH) in the condenser

•         3-4: Isentropic expansion from state 3 (saturated liquid)

•         4-1: Heat absorption (QL) in the evaporator

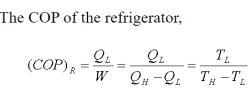
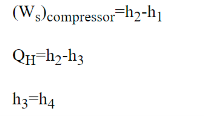
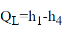
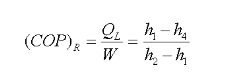
Q7) A Steam enters the throttling calorimeter at 10 MPa and exits at 0.05 MPa and 100°C. Calculate the dryness fraction of steam.

A7)

Dryness fraction is 0.968.

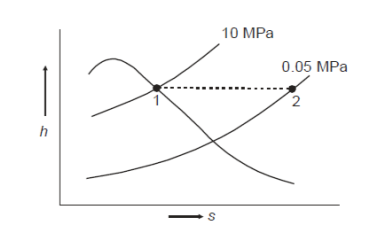
Q8) A feed water pump is used to pump water from 30°C to 200 kPa at a pressure of 200 kPa. Calculate the change in enthalpy assuming that water is incompressible, and that pumping is an isentropic process.

A8)

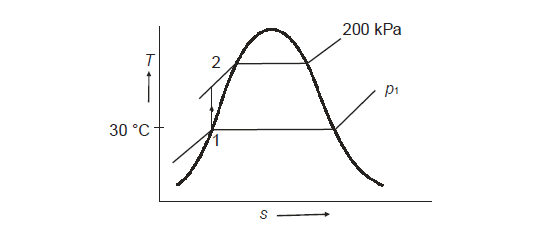
Q9) A rigid vessel contains a liquid-vapour mixture in a 3:2 volume ratio. If the volume of the vessel is 2 m3 and the initial temperature is 150°C, calculate the quality of the water vapour mixture and total mass of fluid in the vessel.

A9)

Q10) The steam turbine expands steam reversibly and adiabatically from 4 MPa and 300°C to 50°C at the turbine exit. Calculate the work output per kilogramme of steam.

A10)

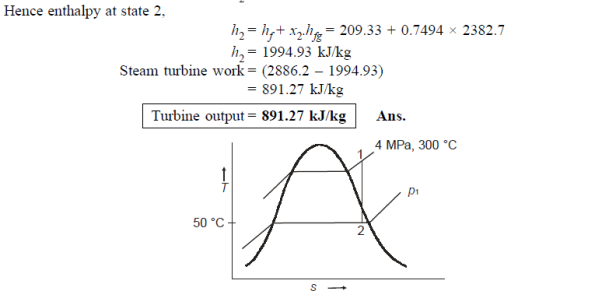
Q11) Bring 100 kg of steam at 100 kPa, 0.5 dry, to a pressure of 1000 kPa inside a closed vessel. Calculate the mass of dry saturated steam admitted at 2000 kPa for pressure increase. Determine the final quality as well.

A11)

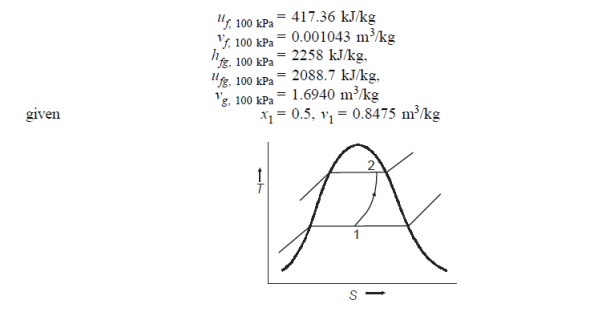
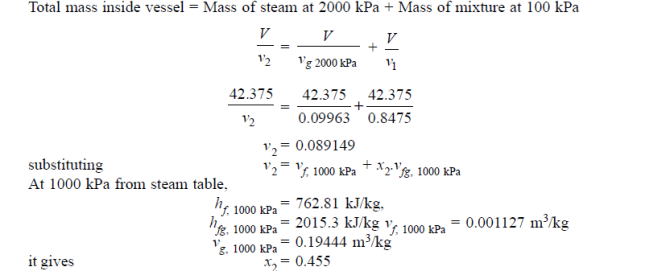
For adiabatic mixing

Q12) A Carnot cycle operates on steam at pressures ranging from 7 MPa to 7 kPa. Calculate the thermal efficiency, turbine work, and compression work per kilogramme of steam.

A12)

Q13) A steam power plant operates at a boiler pressure of 5 MPa, dry saturated, and a condenser pressure of 5 kPa, with steam as the working fluid. Determine the cycle efficiency for (a) Carnot cycle

(b) Rankine cycle. Also show the T-s representation for both the cycles.

A13)

Q14) With air as the working fluid, a basic ideal Brayton cycle has a pressure ratio of 10. At 520 R, the air enters the compressor, and at 2000 R, it enters the turbine. Determine (a) the air temperature at the compressor exit, (b) the back work ratio, and (c) the thermal efficiency while accounting for the changing of specific heats with temperature.

A14)

Q15) The pressure ratio of a simple Brayton cycle utilising air as the working fluid is 8. The cycle's minimum and highest temperatures are 310 and 1160 K, respectively. Determine (a) the air temperature at the turbine exit, (b) the net work production, and (c) the thermal efficiency, assuming an isentropic efficiency of 75 percent for the compressor and 82 percent for the turbine.

A15)

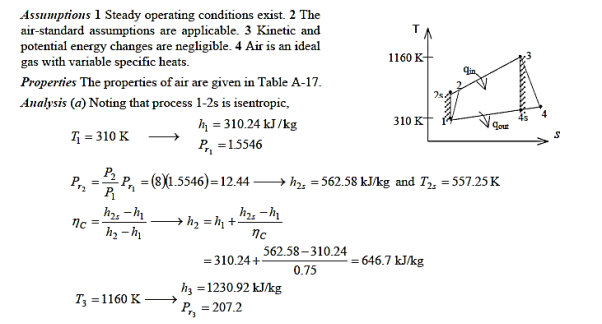
Q16) In a simple ideal Brayton cycle with a pressure ratio of 12, a compressor intake temperature of 300 K, and a turbine inlet temperature of 1000 K, air is employed as the working fluid. Calculate the needed air mass flow rate for a net power output of 70 MW, assuming isentropic efficiency of (a) 100% and (b) 85% for the compressor and turbine, respectively. At room temperature, assume constant specific heats.

A16)

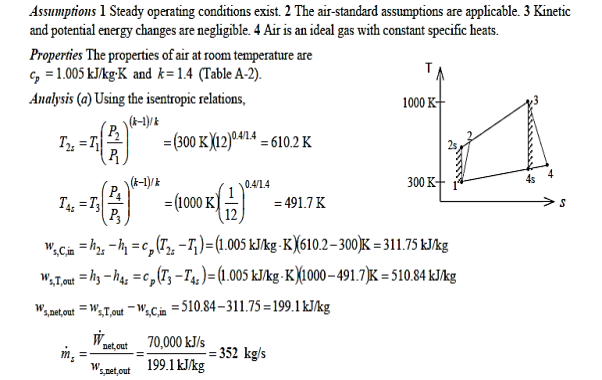
Q17) A stationary gas-turbine power plant uses air as the working fluid in a basic ideal Brayton cycle. The air is 95 kPa and 290 K when it enters the compressor, and 760 kPa and 1100 K when it enters the turbine. 35,000 kJ/s of heat is transmitted to the air. Calculate the power delivered by this plant (a) assuming constant specific heats at room temperature and (b) accounting for temperature-dependent specific heats.

A17)

Q18) At 300 K and 100 kPa, air enters the compressor of a gas-turbine engine, where it is compressed to 700 kPa and 580 K. Before entering the turbine, heat is transmitted to air in the amount of 950 kJ/kg. Determine (a) the fraction of the turbine work output used to operate the compressor and (b) the thermal efficiency for a turbine efficiency of 86 percent. Assume that the specific temperatures of air are varied.

A18)

Q19) A gas-turbine power plant uses air as the working fluid in a simple Brayton cycle. At 120 psi and 2000 R, the air enters the turbine and exits at 15 psi and 1200 R. At a rate of 6400 Btu/s, heat is rejected to the environment, and air flows through the cycle at a rate of 40 lbm/s. Determine the plant's net power production assuming the turbine is isentropic, and the compressor has an isentropic efficiency of 80%. Consider the temperature's effect on specific heats.

A19)

Q20) A gas-turbine power plant produces 32 MW of electricity using the simple Brayton cycle with air as the working fluid. The cycle's minimum and maximum temperatures are 310 and 900 K, respectively, and the air pressure at the compressor outlet is 8 times that at the compressor inlet. Calculate the mass flow rate of air through the cycle using an isentropic efficiency of 80% for the compressor and 86 percent for the turbine. Take into account the temperature's effect on specific heats.

A20)