Unit - 4

Involute and cycloidal gear profiles

Q1) What is Involute Gear Profile?

A1) Involute Gear Profile

Involute profile is obtained by the locus of a point on a straight line when it rolls about a circumference of a circle without slipping. The circle about which the straight-line rolls is known as the base circle. Figure 2 shows the generation of involute profile in which the line BD is rolling about the base circle with center O and the path ABC shows the involute profile traced by the line.                                    

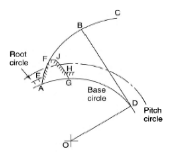
Figure 1. Involute profile

Q2) What is Cycloidal Profile?

A2) Cycloidal profile is obtained by the locus of a point on the circumference of a circle when it rolls on a straight line without slipping. Gear tooth are made by two kind of cycloidal profiles. Face of gear tooth have epicycloid profile while flank have hypocycloid profile. Figure 3 shows the cycloidal profile of gear teeth.

Epicycloid profile is obtained by the locus of a point on the circumference of a circle when it rolls on the circumference of another circle without slipping, while hypocycloid profile is obtained by the locus of a point the circumference of a circle when it rolls inside the circumference of another circle.

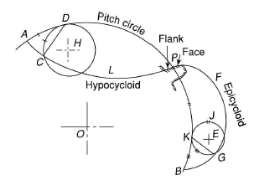
Figure 2. Cycloidal Profile of gear teeth

Q3) Describe all the characteristics of gears?

A3) Characteristics of Gears by Type

“A” indicates advantageous characteristics and “D” indicates disadvantageous characteristics

Q4) What are the gear parameters?

A4)

Gear parameters listed below.

1. Path of contact
2. Arc of contact
3. Contact ratio

Path of contact

In order to calculate the path of contact of gear consider the figure 4 which shows the two gears in contact. In which smaller gear is termed as the pinion while lager gear is known as the wheel.

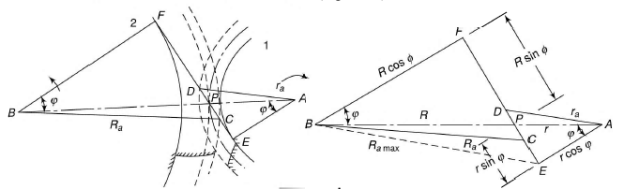
Figure 3. Two gears in contact

Path of contact is given by the line CD shown in the figure 4. In the given figure:

R = radius of pitch circle for the wheel

r = radius of pitch circle for pinion

Ra = radius of addendum circle for wheel

ra = radius of addendum circle for pinion

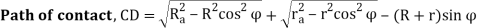
Arc of contact

Arc of contact is the path on the pitch circle of pinion and the wheel from start of their engagement to the end of the disengagement. The arc of contact is calculated by the given formula.

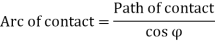
Contact ratio

It is also known as the number of pairs of teeth in contact during meshing of a pair of gears. During the meshing of teeth all the teeth lying in between the arc of contact are the number of pairs of teeth in contact. We can define the contact ratio as the ratio of arc of contact to the circular pitch.

Q5) Explain fundamental law of gearing and conjugate action?

A5)

This law states the necessary condition for the constant angular velocity for two mating gears i.e. the common normal at the point of contact of the gears in mesh must pass through the pitch point, and the ration in which the pitch point divides the common normal is the inverse ratio of the angular velocity of the mating gears.

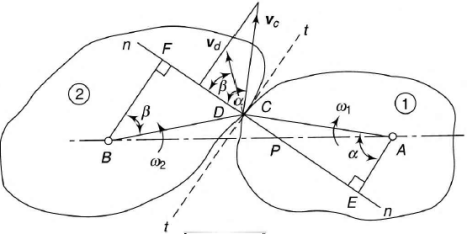
Figure 4. Gear teeth profile in mesh

Consider the figure.5 in which point C and D are the contact point on gear 1 and 2 respectively, line n-n is the common normal at the point of contact and point P is the pitch point. So, the necessary condition for the constant angular velocity is:

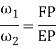
Where, 1= angular velocity of gear 1.

2= angular velocity of gear 2.

Conjugate Action

If the meshing gears are shaped in such a way that they produce a constant angular velocity ratio, such surfaces are termed as conjugate surfaces. This act of producing constant angular velocity ratio by two meshing gear is known as conjugate action.

Q6) What is spur contact ratio?

A6)

Spur gears or directly-reduce gears are the only kind of equipment. They encompass a cylinder or disk with tooth projecting radially. Viewing the equipment at ninety stages from the shaft duration (aspect on) the teeth faces are directly and aligned parallel to the axis of rotation. Looking down the duration of the shaft, a teeth's pass phase is commonly now no longer triangular. Instead of being directly (as in a triangle) the edges of the pass phase have a curved form (commonly involute and much less typically cyclical) to reap a steady pressure ratio. Spur gears mesh collectively effectively best if suited for parallel shafts

No axial thrust is created with the aid of using the teeth loads. Spur gears are exceptional at slight speeds however have a tendency to be noisy at excessive speeds. Spur equipment may be categorized into stress angles, 20° being the modern-day enterprise popular and 14½° being the former (frequently located in older equipment). Spur equipment tooth are synthetic as both involute profile and cycloidal profile. When gears are in mesh it's far feasible that an involute element of 1 will touch a non-involute part of the opposite equipment.

Q7) What is interface/undercutting?

A7)

Locking of meshed gear teeth due non-conjugate or non-involute profile is termed as the interference. Non-conjugate gear teeth profile causes improper sliding of gear teeth which results in rough action and binding. Rough action and binding cause different sliding velocity of mating gears and results in locking.

Minimum number of teeth to avoid interference

• For wheel

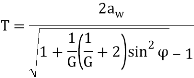
• For pinion

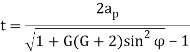
Undercutting

In case of involute gear profile addendum of mating gears removes some part in the dedendum if there is interference. This removed portion in the dedendum is known as the undercut and the process of removal of the material from at the root of gears is known as undercutting. Figure 6 shows the undercutting in the gears.

Q8) Explain helical gears?

A8)

Helical Gear:

The tooth of a helical tools are set at an attitude (relative to axis of the tools) and take the form of a helix. This lets in the tooth to mesh gradually, beginning as factor touch and growing into line touch as engagement progresses. One of the maximum considerable advantages of helical gears over spur gears is much less noise, in particular at medium- to high-speeds. Also, with helical gears, a couple of tooth are usually in mesh, because of this that much less load on every character enamel.

This consequences in a smoother transition of forces from one enamel to the next, in order that vibrations, surprise loads, and put on are reduced. But the willing attitude of the tooth additionally reasons sliding touch among the tooth, which produces axial forces and heat, reducing efficiency. These axial forces play a good sized position in bearing choice for helical gears. Because the bearings need to resist each radial and axial forces, helical gears require thrust or curler bearings, that are commonly large (and extra expensive) than the easy bearings used with spur gears.

The axial forces range in percentage to the significance of the tangent of the helix attitude. Although large helix angles offer better pace and smoother motion, the helix attitude is commonly constrained to forty five ranges because of the manufacturing of axial forces.

Q9) Explain bevel gears?

A9)

Two vital ideas in gearing are pitch floor and pitch attitude. The pitch floor of a equipment is the imaginary toothless floor which you could have through averaging out the peaks and valleys of the person tooth. The pitch floor of an regular equipment is the form of a cylinder. The pitch attitude of a equipment is the attitude among the face of the pitch floor and the axis. The maximum acquainted forms of bevel gears have pitch angles of much less than ninety tiers and consequently are cone-shaped.

This kind of bevel equipment is known as outside due to the fact the equipment tooth factor outward. The pitch surfaces of meshed outside bevel gears are coaxial with the equipment shafts; the apexes of the 2 surfaces are on the factor of intersection of the shaft axes. The use of a proper bevel equipment has even extra significance for the reliability of the axle than some other spare part. Bevel gears which have pitch angles of extra than 90 tiers have tooth that factor inward and are known as inner bevel gears. Bevel gears which have pitch angles of precisely ninety tiers have tooth that factor outward parallel with the axis and resemble the factors on a crown. That's why this kind of bevel equipment is known as a crown equipment.

Q10) Explain worm gear?

A10)

The factors also are known as the bug screw and bug equipment. The terminology is regularly burdened with the aid of using obscure use of the time period bug equipment to consult the bug, the bug wheel, or the bug force as a unit.

The bug force later seemed with inside the Indian subcontinent, to be used in curler cotton gins, throughout the Delhi Sultanate with inside the 13th or fourteenth centuries A gearbox designed the use of a bug and bug wheel is significantly smaller than one crafted from undeniable spur gears, and has its force axes at 90° to every other.

With a single-begin bug, for every 360° flip of the bug, the bug wheel advances with the aid of using most effective one enamel. Therefore, no matter the bug's length (practical engineering limits notwithstanding), the equipment ratio is the "length of the bug wheel - to - 1". Given a single-begin bug, a 20-enamel bug wheel reduces the velocity with the aid of using the ratio of 20:1. With spur gears, a equipment of 12 tooth ought to healthy with a 240-enamel equipment to reap the equal 20:1 ratio. Therefore, if the diametrical pitch (DP) of every equipment is the equal, then, in phrases of the bodily length of the 240 enamel equipment to that of the 20 enamel equipment, the bug association is significantly smaller in volume.

Q11) Explain spur gear contact ratio?

A11)

To assure continuous smooth tooth action, as one pair of teeth ceases action a succeeding pair of teeth must already have come into engagement. It is desirable to have as much overlap as is possible. A measure of this overlap action is the contact ratio. This is a ratio of the length of the line-of-action to the base pitch. Figure shows the geometry for a spur gear pair, which is the simplest case, and is representative of the concept for all gear types. The length-of-action is determined from the intersection of the line-of-action and the outside radii. The ratio of the length-of-action to the base pitch is determined from:

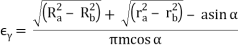
It is good practice to maintain a contact ratio of 1.2 or greater. Under no circumstances should the ratio drop below 1.1, calculated for all tolerances at their worst case values.

Q12) Explain undercutting?

A12)

Locking of meshed gear teeth due non-conjugate or non-involute profile is termed as the interference. Non-conjugate gear teeth profile causes improper sliding of gear teeth which results in rough action and binding. Rough action and binding cause different sliding velocity of mating gears and results in locking.

• Use of a larger pressure angle (having a larger pressure angle results in a smaller base circle. As a result, more of the tooth profiles become involute)
• Under-cutting of tooth (A portion of teeth below the base circle is cut off. When teeth are produced by this process, the tip of one tooth of a gear will not contact the non-involute portion of the tooth of other gear)
• Tooth stubbing (In this process a portion of the tip of the teeth is removed, thus preventing that portion of the tip of tooth in contacting the non-involute portion of the other meshing tooth).
• Increasing the number of teeth on the gear can also eliminate the chances of interference.
• Increasing slightly the center distance between the meshing gears would also eliminate interference.
• Tooth profile modification or profile shifting (Using profile shifted gears (gears with non-standard profile) can also be an option to eliminate interference. In profile shifted meshing gears, the addendum on the pinion is shorter compared with standard gears).

Q13) What is epicyclic gear train kinematics?

A13)

An epicyclic tools teach (additionally called a planetary gearset) includes gears established in order that the middle of 1 tools revolves across the middle of the different.

A service connects the facilities of the 2 gears and rotates the planet and solar gears mesh in order that their pitch circles roll without slip. A factor at the pitch circle of the planet tools strains an epicycloid curve. In this simplified case, the solar tools is constant and the planetary tools(s) roll across the solar tools.

An epicyclic tools teach may be assembled so the planet tools rolls at the interior of the pitch circle of a constant, outer tools ring, or ring tools, on occasion known as an annular tools. In this case, the curve traced via way of means of a factor at the pitch circle of the planet is a hypocycloid. The aggregate of epicycle tools trains with a planet enticing each a solar tools and a hoop tools is known as a planetary tools teach.

Q14) Explain regular gear kinematics?

A14)

An epicyclical tools educate (additionally referred to as a planetary gear set) includes gears installed in order that the middle of 1 tools revolves across the middle of the different.

An epicyclical tools educate may be assembled so the planet tools rolls at the internal of the pitch circle of a constant, outer tools ring, or ring tools, every now and then known as an annular tools. In this case, the curve traced with the aid of using a factor at the pitch circle of the planet is a hypocycloid.

Typically, the planet gears are installed on a movable arm or service, which itself can also additionally rotate relative to the solar tools. Epicyclic gearing structures additionally contain the usage of an outer ring tools or annulus, which meshes with the planet gears. Planetary gears (or epicyclic gears) are generally labeled as easy or compound planetary gears.