Unit - 2

Heat Convection

Q1) Given:  Nitrogen gas at 0°C is flowing over a 1.2 m long, 2 m wide plate maintained at 80°C with a velocity of 2.5 m/s. For nitrogen, r = 1.142 kg/m3, cp = 1.04 kJ/kgK, n = 15.63 x 10–6 m2/s and k = 0.0262 W/mK.

To find: (a) The average heat transfer coefficient and (b) the total heat transfer from the plate.

A10

Q2) Air at 20°C and at atmospheric pressure flows at a velocity of 4.5 m/s past a flat plate with a sharp leading edge. The entire plate surface is maintained at a temperature of 60°C. Assuming that the transition occurs at a critical Reynolds number of 5 x 105, find the distance from the leading edge at which the boundary layer changes from laminar to turbulent. At the location, calculate the following:

(i)                Thickness of hydrodynamic boundary layer,

(ii)              Thickness of thermal boundary layer,

(iii)           Local and average convective heat transfer coefficients,

(iv)            Heat transfer rate from both sides per unit width of plate,

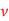Assume cubic velocity profile and approximate method. Thermo-physical properties of air at mean film temperature of 40°C are: = 1.128 kg/m3, = 16.96 x 10–6 m3/s, k = 0.02755 W/mK and Pr = 0.7.

A2)

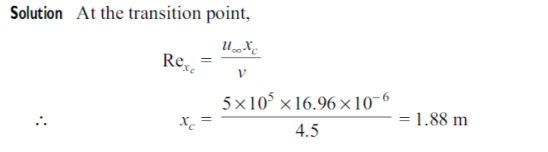
Q3) Air at 20°C and 1 atm flows over a flat plate at 40 m/s. The plate is 80 cm long and is maintained at 60°C. Assuming unit depth in z-direction, calculate the heat transfer rate from the plate. Properties of air at 40°C are: Pr = 0.7, k = 0.02723 W/m K, cp = 1.007 kJ/kg K and = 1.906 x 10–5 kg/ms.

A3)

Q4) Given: Water at 10°C flows over a flat plate (at 90°C) measuring 1 m x 1 m, with a velocity of 2 m/s. Properties of water at 50°C are = 988.1kg/m3, 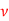= 0.556 x 10–6 m2/s, Pr = 3.54 and k = 0.648 W/mK. To find: (a) The length of plate over which the flow is laminar, (b) the rate of heat transfer from the entire plate.

A4)

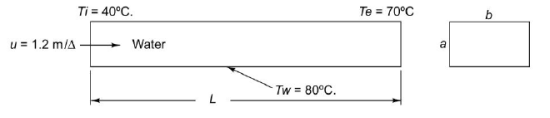
Q5) Water is heated while flowing through a 1.5 cm x 3.5 cm rectangular cross-section tube at a velocity of 1.2 m/s. The entering temperature of the water is 40°C, and the tube wall is maintained at 85°C. Determine the heat transfer coefficient. Properties of water at the mean bulk temperature of 55°C are: = 985.5 kg/m3; cp = 4.18 kJ/kg K, 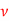= 0.517 x 10–6 m2/s, k = 0.654 W/m K and Pr = 3.26.

A5)

Q6) Air at 20°C and a pressure of 1 bar is flowing over a flat plate at a velocity of 3 m/s. If the plate is 280 mm wide and at 56°C, estimate the following quantities at x = 280 mm, given that the properties of air at the bulk mean temperature of 38°C are: = 1.1374 kg/m3, k = 0.02732 W/mK, cp = 1.005 kJ/kgK, and 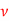= 16.768 x 10–6 m2/s:

(i)boundary layer thickness, (ii) local friction coefficient, (iii) average friction coefficient, (iv) shearing stress due to friction, (v) thickness of thermal boundary layer, (vi) local convective heat transfer coefficient, (vii) average convective heat transfer coefficient, (viii) rate of heat transfer by convection.

A6)

Q7) A metal plate 0.609 m in height forms the vertical wall of an oven and is at a temperature of 171 °C. Within the oven is air at a temperature of 93.4 °C and atmospheric pressure. Assuming that natural convection conditions hold near the plate, and that for this case Nu = 0.548 (Gr Pr)1/4

Find the mean heat transfer coefficient and the heat taken up by air per second per metre width. For air at 132.2°C, take k = 33.2 x 10–6 kW/m K, = 0.232 x 10–4 kg/ms, cp = 1.005 kJ/kg K. Assume air as an ideal gas and R = 0.287 kJ/kg K.

A7)

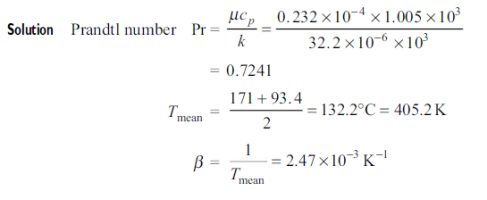
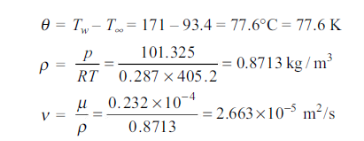
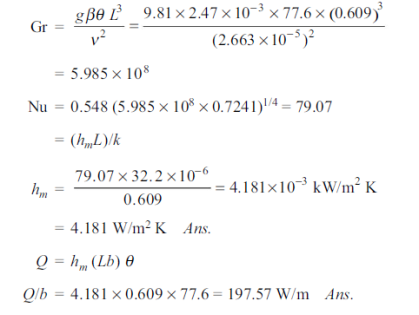
Q8) Given: A 0.15 m outer diameter of steel pipe lies 2 m vertically and 8 m horizontally in a large room with an ambient temperature of 30°C. The pipe surface is at 250°C and has an emissivity of 0.60. To estimate: The total rate of heat loss from the pipe to the atmosphere.

A8)

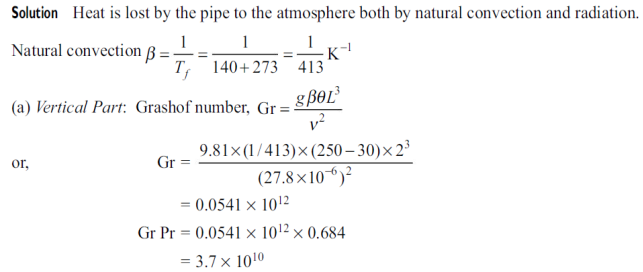
Since Gr.Pr > 109, the flow is turbulent over the pipe.

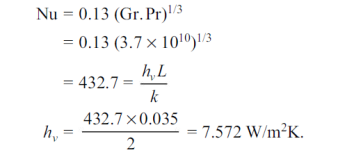
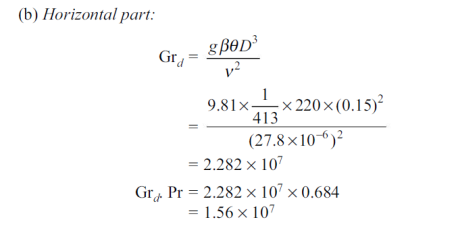
Since Grd. Pr < 2 x 107, the flow is laminar.

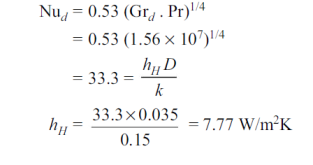
Q9) A nuclear reactor with its core constructed of parallel vertical plates 2.2 m high and 1.45 m wide has been designed on free convection heating of liquid bismuth. The maximum temperature of the plate surfaces is limited to 960°C, while the lowest allowable temperature of bismuth is 340°C. Calculate the maximum possible heat dissipation from both sides of each plate. For the convection coefficient the appropriate correlation is

Nu = 0.13 (Gr.Pr)1/3

Where the properties evaluated at the mean film temperature of 650°C for bismuth are: = 104 kg/m3, = 3.12 kg/m-h, cp = 150.7 J/kgK, k = 13.02 W/mK.

A9)

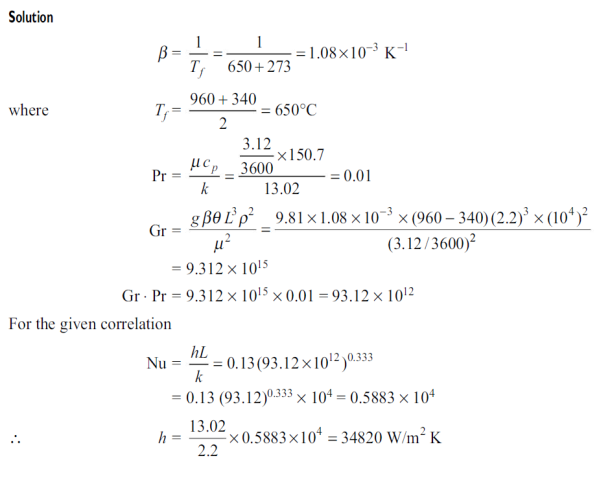
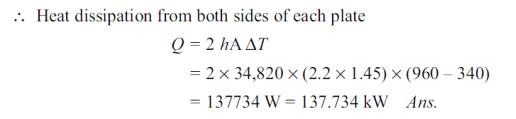
Q10) The maximum allowable surface temperature of an electrically heated vertical plate 15 cm high and 10 cm wide is 140°C. Estimate the maximum rate of heat dissipation from both sides of the plate in an atmosphere at 20°C. The radiation heat transfer coefficient is 8.72 W/m2 K. For air at 80°C, take n = 21.09 x 10–6 m2/s, Pr = 0.692 and k = 0.03 W/m K.

A10)

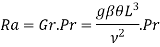
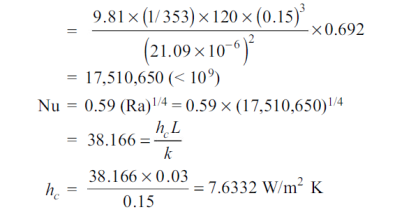
As heat transfer takes place from both the sides

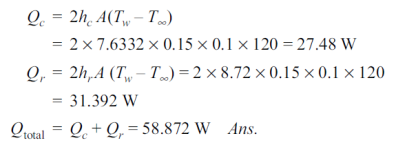
Q11) Differentiate between forced and natural convection.

A11)