|
 are constant.The term containing the highest power of x are called the leading termThe degree of the polynomial is the power of x in the leading term degree 0, 1, and 2 are polynomials which are constant, linear and quadratic functions while degree 3, 4, and 5 are polynomials with special names: cubic, quartic, and quintic functions. Polynomials with degree n > 5 are just called
are constant.The term containing the highest power of x are called the leading termThe degree of the polynomial is the power of x in the leading term degree 0, 1, and 2 are polynomials which are constant, linear and quadratic functions while degree 3, 4, and 5 are polynomials with special names: cubic, quartic, and quintic functions. Polynomials with degree n > 5 are just called 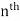 degree polynomials. Constant Function: A constant function is a linear function for which the range does not change no matter which member of the domain is used. Linear Function: Linear functions are those whose graph is a straight line.A linear function has the following form. y = f(x) = a + bx.Quadratic Function: A quadratic function is one of the forms: f(x) =
degree polynomials. Constant Function: A constant function is a linear function for which the range does not change no matter which member of the domain is used. Linear Function: Linear functions are those whose graph is a straight line.A linear function has the following form. y = f(x) = a + bx.Quadratic Function: A quadratic function is one of the forms: f(x) =  , where a, b, and c are numbers with a ≠ 0 Power Function: A power function is a function that can be represented inthe form:
, where a, b, and c are numbers with a ≠ 0 Power Function: A power function is a function that can be represented inthe form: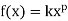 where k and pare real numbers, and x is known as the coefficientRational Function-A rational function is defined by a rational fraction, i.e., an algebraic fraction such that both the numerator and the denominator are polynomials.Note- the value of denominator should not be equal to zero. Q2) Find the domain and range of the function f(x) =
where k and pare real numbers, and x is known as the coefficientRational Function-A rational function is defined by a rational fraction, i.e., an algebraic fraction such that both the numerator and the denominator are polynomials.Note- the value of denominator should not be equal to zero. Q2) Find the domain and range of the function f(x) =  A2)f(0) = 3/-3 = -1f(1) = -1f(2) = -1f(3) = -1so that the domain is = {-1, 0, 1, 2, 4,….} and range = {-1, -1, -1, -1,…..} Q3) Find the value of f(2), f(0) and f(3) of the given function-
A2)f(0) = 3/-3 = -1f(1) = -1f(2) = -1f(3) = -1so that the domain is = {-1, 0, 1, 2, 4,….} and range = {-1, -1, -1, -1,…..} Q3) Find the value of f(2), f(0) and f(3) of the given function-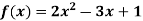 A3)
A3)
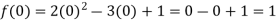
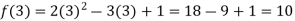 Q4) If f(x) =
Q4) If f(x) = 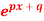 then prove that
then prove that 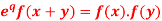 A4)
A4)By taking LHS-
Hence proved |
then
y = 25 + 5(1) = 30let x = 3
then
y = 25 + 5(3) = 40
|
What is total cost at varying levels of output?let x = units of output
let C = total costC = fixed cost plus variable cost = 7,000 + 600 x
output | total cost |
15 units | C = 7,000 + 15(600) = 16,000 |
30 units | C = 7,000 + 30(600) = 25,000 |
 Combinations of linear equationsLinear equations can be added together, multiplied or divided.A simple example of addition of linear equationsC(x) is a cost functionC(x) = fixed cost + variable costR(x) is a revenue functionR(x) = selling price (number of items sold)profit equals revenue less costP(x) is a profit functionP(x) = R(x) - C(x)x = the number of items produced and sold Data:A company receives $45 for each unit of output sold. It has a variable cost of $25 per item and a fixed cost of $1600.
Combinations of linear equationsLinear equations can be added together, multiplied or divided.A simple example of addition of linear equationsC(x) is a cost functionC(x) = fixed cost + variable costR(x) is a revenue functionR(x) = selling price (number of items sold)profit equals revenue less costP(x) is a profit functionP(x) = R(x) - C(x)x = the number of items produced and sold Data:A company receives $45 for each unit of output sold. It has a variable cost of $25 per item and a fixed cost of $1600.What is its profit if it sells (a) 75 items, (b)150 items, and (c) 200 items?
R(x) = 45x | C(x) = 1600 + 25x | ||
P(x) = 45x -(1600 + 25x) |
| ||
= 20x - 1600 |
| ||
let x = 75 | P(75) = 20(75) - 1600 = -100 a loss | ||
let x = 150 | P(150) = 20(150) - 1600 = 1400 | ||
let x = 200 | P(200) = 20(200) - 1600 = 2400 | ||
5x -2y = 7
The coefficient of y in Equation 1 is 1. So first we make y the subject of Equation 1:
y = 13 - 3x
Next, substitute this expression for y in Equation 2 and solve for x:
5x - 2(13 - 3x) = 7 | Multiply out bracket |
5x - 26 + 6x = 7 | Combine like terms (x's on one side, numbers on the other) |
11x = 33 | Divide both sides by 11 to solve for x |
x = 3 |
|
y = 13 - 3(3) = 4
y = 4
So the solution to the pair of simultaneous linear equations is (3,4).
2. 2x + 4y = 10
2x + y = 4
The coefficient of y in Equation 2 is 1. So first we make y the subject of Equation 2:
y = 4 - 2x
Next, substitute this expression for y in Equation 1 and solve for x:
2x + 4(4 - 2x) = 10 | Multiply out bracket |
2x + 16 - 8x = 10 | Combine like terms (x's on one side, numbers on the other) |
-6x = -6 | Divide both sides by -6 to solve for x |
x = 1 |
|
Finally, substitute the solution for x into the expression for y:
y = 4 - 2(1) = 2
y = 2
So the solution to the pair of simultaneous linear equations is (1,2).
3. x - 5y = 7
2x -4y = 8
The coefficient of x in Equation 1 is 1. So first we make x the subject of Equation 1:
x = 7 + 5y
Next, substitute this expression for x in Equation 2 and solve for y:
2(7 + 5y) - 4y = 8 | Multiply out bracket |
14 + 10y - 4y = 8 | Combine like terms (y's on one side, numbers on the other) |
6y = -6 | Divide both sides by 6 to solve for y |
y = -1 |
|
Finally, substitute the solution for y into the expression for x:
x = 7 + 5(-1) = 2
x = 2
So the solution to the pair of simultaneous linear equations is (2,-1).
4. 2x + 4y = 12
x + 8y = 30
The coefficient of x in Equation 2 is 1. So first we make x the subject of Equation 2:
x = 30 - 8y
Next, substitute this expression for x in Equation 1 and solve for y:
2(30 - 8y) + 4y = 12 | Multiply out bracket |
60 - 16y + 4y = 12 | Combine like terms (y's on one side, numbers on the other) |
-12y = -48 | Divide both sides by -12 to solve for y |
y = 4 |
|
Finally, substitute the solution for y into the expression for x:
x = 30 - 8(4) = -2
x = -2
So the solution to the pair of simultaneous linear equations is (-2,2).
5. 2x - 4y = 10
-4x+5y = -26
None of the coefficients are 1. So we can choose to make any variable the subject.
Let’s make x the subject of Equation 1:
x = (10 + 4y)/2
x = 5 + 2y
Next, substitute this expression for x in Equation 2 and solve for y:
-4(5 + 2y ) + 5y = -26
-20 - 8y + 5y = -26
-3y = -6
y = 2
Finally, substitute the solution for y into the expression for x:
x = 5 + 2(2) = 9
x = 9
So the solution to the pair of simultaneous linear equations is (9,2).
6. 6x + 2y = 10
10x - 3y = 12
None of the coefficients are 1. So we can choose to make any variable the subject.
Let’s make y the subject of Equation 2:
y = (12-10x)/(-3)
y = -4 + (10/3) x
Next, substitute this expression for y in Equation 1 and solve for x:
6x + 2(-4 + (10/3) x) = 10
6x - 8 + (20/3) x = 10
(38/3) x = 18
x = 18*(3/38) = 27/19
Finally, substitute the solution for x into the expression for y:
y = -4 + (10/3)/(27/19) = -4 + 270/57 = -228/57 = 270/57 = 42/57 = 14/19
So the solution to the pair of simultaneous linear equations is (27/19,5/19) Q16) Solve the following simultaneous equations by using the elimination method:
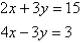 A16)Label the equations as follows:
A16)Label the equations as follows: Notice that 3y appears on the left-hand side of both equations. Adding the left-hand side of (1) and (2), and then the right-hand sides, gives:
Notice that 3y appears on the left-hand side of both equations. Adding the left-hand side of (1) and (2), and then the right-hand sides, gives: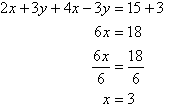 Note:We have added equals to equals, and addition eliminates y.
Note:We have added equals to equals, and addition eliminates y.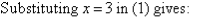
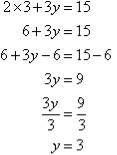
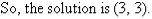 Q17) Solve the following simultaneous equations by using the elimination method:
Q17) Solve the following simultaneous equations by using the elimination method: A17)Label the equations as follows:
A17)Label the equations as follows: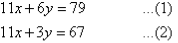
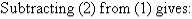
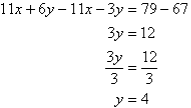
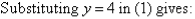
 So, the solution is (5, 4)
So, the solution is (5, 4)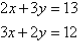 A18)Label the equations as follows:
A18)Label the equations as follows: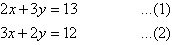 Multiplying (1) by 2 and (2) by 3 gives:
Multiplying (1) by 2 and (2) by 3 gives: Subtracting (3) from (4) gives:
Subtracting (3) from (4) gives: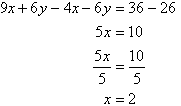
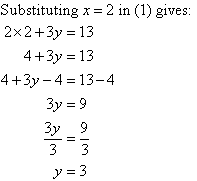 So, the solution is (2, 3).
So, the solution is (2, 3).

