Unit 3
Dispersion and Skewness
Question Bank
- Define Dispersion. State its features.
Answer: Central tendency do not reveal the variability present in the data. Dispersion measures the scatteredness of the data series around its average. It tells the variation of the data from one another and gives a clear idea about the distribution of the data.
In statistics, dispersion is extent to which a distribution is stretched or squeezed.
Features of measures of dispersion
- It should be rigidly defined
- It should be easy to understand and calculate
- Must be based on all observation of the data
- Must be less affected by sampling fluctuation
2. What are its types?
Answer: The different types of measures of dispersion:

Algebraic measures – It includes the mathematical way to calculate the measures of dispersion.
Graphical measures – The way to calculate the measures of dispersion by graphs and figures.
Absolute measures of dispersion – It gives an idea about the amount of dispersion in a set of observations. It measures the dispersion in the same units as the units of original data. Absolute measures cannot be used for comparison of two or more data set variations.
Relative measures of dispersion – The relative measures of distribution are used for comparing the distribution of two or more data sets.
3. Explain the concept of Skewness.
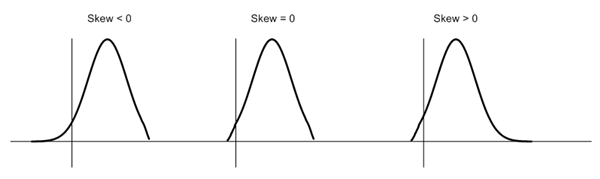
Answer: Skewness is a measure of symmetry or lack of symmetry in a distribution. A distribution is symmetric if it looks same both its left and right side. The skewness for normal distribution is Zero. Negative values for skewness indicate that the data are skewed left and positive values for skewness indicate that the data are skewed right. For small data sets, this measure is unreliable. The below diagram shows how a normal distribution curve looks like in different situation of skewness:
The formula for measuring Coefficient of Skewness as given by Karl Pearson is as under:
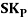 =
= 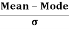
Where,  = Karl Pearson’s Coefficient of Skewness
= Karl Pearson’s Coefficient of Skewness
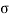 = Standard Deviation
= Standard Deviation
The formula for measuring Co-efficient of Skewness as given by Bowley is as under:

4. What do you mean by Standard Deviation?
Answer: Standard deviation is calculated as square root of average of squared deviations taken from actual mean. It is also called root mean square deviation. This measure suffers from less drawbacks and provides accurate results. It removes the drawbacks of ignoring algebraic sign. We square the deviation to make them positive.
Two ways of computing SD
- Direct method

- Shortcut method
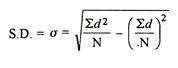
d = Deviation of the score from an assumed mean, say AM; i.e. d = (X – AM). AM is assumed mean
d2 = the square of the deviation.
∑d = the sum of the deviations.
∑d2 = the sum of the squared deviations.
N = No. Of the scores
5. What is Co-efficient of Variation?
Answer: Standard Variation is an absolute measure of dispersion. When comparison between two series has to be made, coefficient of variation is used. Coefficient of variation is a statistical measure of the dispersion of data with respect to mean.

Where, σ = Standard Deviation
µ = Mean
6. What is the range for the following set of numbers?
15,21,57,43,11,39,56,83,77,11,64,91,18,37
Solution:
Range = H-L
= 91 – 11 = 80
Therefore, the range is 80
7. The frequency table shows the number of goals the lakers scored in their last twenty matches. What was the range?
No. Of goals | Frequency |
0 | 2 |
1 | 3 |
2 | 3 |
3 | 6 |
4 | 3 |
5 | 1 |
6 | 1 |
7 | 1 |
Solution:
The range is the difference between the lowest and highest values.
The highest value was 7 (They scored 7 goals on 1 occasion)
The lowest value was 0 (They scored 0 goals on 2 occasions)
Therefore, the range = 7 - 0 = 7
8. Find the interquartile for the following data set: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
Solution:
Arrange the numbers in ascending order
3, 5, 7, 8, 9, 11, 15, 16, 20, 21
Make a mark in the center of the data:
(3, 5, 7, 8, 9,) | (11, 15, 16, 20, 21)
Find the median
Q1 = 7
Q3 = 16
Interquartile range = 16 – 7 = 9
9. Calculate quartile deviation from the following test scores:
Sl. N o | Test scores |
1 | 17 |
2 | 17 |
3 | 26 |
4 | 27 |
5 | 30 |
6 | 30 |
7 | 31 |
8 | 37 |
Solution:
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (8 + 1) /4] th observation
Q1 = 2.25 th observation
Thus, 2.25 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 17 and 26
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 17 + 0.75 * (26 – 17) = 23.75
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (8 + 1) /4] th observation
Q3 = 6.75 th observation
So, 6.75 th observation lies between the 6th and 7th value in the ordered group, between frequency 30 and 31
Third quartile (Q3) is calculated as
Q3 = 6th observation +0.25 * (7th observation – 6th observation)
Q3 = 30 + 0.25 * (31 – 30) = 30.25
Now using the quartiles values Q1 and Q3, we will calculate the quartile deviation.
QD = (Q3 - Q1) / 2
QD = (30.25 – 23.75) / 2 = 3.25
10. Calculate Quartile Deviation
Age in years | 40 -44 | 45 – 49 | 50 – 54 | 55 - 59 | 60 – 64 | 65 - 69 |
Employees | 5 | 8 | 11 | 10 | 9 | 7 |
Solutions:
In the case of Frequency Distribution, Quartiles can be calculated by using the formula:
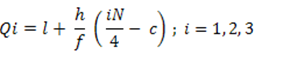
Class interval | F | Class boundaries | CF |
40 -44 | 5 | 39.5 – 44.5 | 5 |
45 – 49 | 8 | 44.5 – 49.5 | 13 |
50 – 54 | 11 | 49.5 – 54.5 | 24 |
55 – 59 | 10 | 54.5 – 59.5 | 34 |
60 – 64 | 9 | 59.5 – 64.5 | 43 |
65 – 69 | 7 | 64.5 – 69.5 | 50 |
Total | 50 |
|
|
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(50)/4]th observation
Q1 = 12.50th observation
So, 12.50th value is in the interval 44.5 – 49.5
Group of Q1 = 44.5 – 49.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (44.5 + ( 5/ 8)* (1* (50/4) – 5)
Q1 = 49.19
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (50) /4] th observation
Q3 = 37.5th observation
So, 37.5th value is in the interval 59.5 – 64.5
Group of Q3 = 59.5 – 64.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (59.5 + ( 5/ 9)* (3* (50/4) – 34)
Q3 = 61.44
QD = (Q3 - Q1) / 2
QD = (61.44 – 49.19) / 2 = 6.13
Coefficient of Quartile Deviation = (Q3 – Q1) / (Q3 + Q1)
= (61.44 – 49.19) /(61.44 + 49.19) = 0.11
11. Computation of mean deviation in ungrouped data
X = 55, 45, 39, 41, 40, 48, 42, 53, 41, 56
Solution:
X |
| Absolute deviation (signed ignored) |
55 | 55 - 46 = 9 | 9 |
45 | 45 – 46 = -1 | 1 |
39 | -7 | 7 |
41 | -5 | 5 |
40 | -6 | 6 |
48 | 2 | 2 |
42 | -4 | 4 |
53 | 7 | 7 |
41 | -5 | 5 |
56 | 10 | 10 |
∑X = 460 |
|
|
Mean = 460/10 = 46
MD = 56/10 = 5.6
12. Calculate Mean Deviation:
Class interval | 15 – 19 | 20 – 24 | 25 – 29 | 30 – 34 | 35 – 39 | 40 – 44 | 45 - 49 |
Frequency | 1 | 4 | 6 | 9 | 5 | 3 | 2 |
Solution:
Class Interval | F | X | FX | D | FD |
15 – 19 | 1 | 17 | 17 | 15 | 15 |
20 – 24 | 4 | 22 | 88 | 10 | 40 |
25 – 29 | 6 | 27 | 162 | 5 | 30 |
30 - 34 | 9 | 32 | 288 | 0 | 0 |
35 - 39 | 5 | 37 | 185 | 5 | 25 |
40 - 44 | 3 | 42 | 126 | 10 | 30 |
45 - 49 | 2 | 47 | 94 | 15 | 30 |
| N = 30 |
| ∑fx = 960 |
|  |
Mean =960/30 = 32
MD = 170 / 30 = 5.667
Coefficient of mean deviation
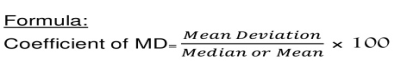
Coefficient of mean deviation = (5.67/32)*100 = 17.71
13. Calculate Standard Deviation: X = 12, 15, 10, 8, 11, 13, 18, 10, 14, 9
Mean = 120/10 = 12
Scores | d | 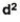 |
12 | 12-12 = 0 | 0 |
15 | 15-12 = 3 | 9 |
10 | 10 -12 = -2 | 4 |
8 | -4 | 16 |
11 | -1 | 1 |
13 | 1 | 1 |
18 | 6 | 36 |
10 | -2 | 4 |
14 | 2 | 4 |
9 | -3 | 9 |
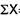 | 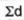 |  |
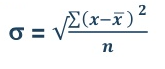
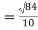 = 2.9
= 2.9
14. Calculate Standard Deviation:
C.I. | 0 - 2 | 3 - 5 | 6- 8 | 9-11 | 12-14 | 15 -17 | 18 - 20 |
F | 1 | 3 | 5 | 7 | 6 | 5 | 3 |
Solution:
C.I | f | Mid-point x | Fx | d | 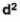 | Fd2 |
0-2 | 1 | 1 | 1 | -10.1 | 102.01 | 102.01 |
3-5 | 3 | 4 | 12 | -7.1 | 50.41 | 151.23 |
6-8 | 5 | 7 | 35 | -4.1 | 16.81 | 84.05 |
9-11 | 7 | 10 | 70 | -1.1 | 1.21 | 8.47 |
12-14 | 6 | 13 | 78 | 1.9 | 3.61 | 21.66 |
15-17 | 5 | 16 | 80 | 4.9 | 24.01 | 120.05 |
18-20 | 3 | 19 | 57 | 7.9 | 62.41 | 187.23 |
| 30 |
| 333 |
|
| 674.70 |
Mean = 333/30 = 11.1
SD =
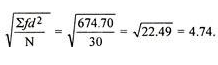
15. Calculate Coefficient of Variation from the following data given below:
Standard Deviation = 4.5 Mean= 12.
Solution: We know,
Coefficient of Variation =  x 100%
x 100%
=  x 100%
x 100%
= 37.5%
16. Calculate Standard Deviation and Co-efficient of Variation.
Class interval | Frequency |
30 – 39 | 3 |
40 – 49 | 1 |
50 – 59 | 8 |
60 – 69 | 10 |
70 – 79 | 7 |
80 – 89 | 7 |
90 – 99 | 4 |
Solution:
Class interval | Frequency | Mid-point x | Fx |
|
|
|
30 – 39 | 3 | 34.5 | 103.5 | -33.5 | 1122.25 | 3366.75 |
40 – 49 | 1 | 44.5 | 44.5 | -23.5 | 552.25 | 552.25 |
50 – 59 | 8 | 54.5 | 436.0 | -13.5 | 182.25 | 1458 |
60 – 69 | 10 | 64.5 | 645.0 | -3.5 | 12.25 | 122.5 |
70 – 79 | 7 | 74.5 | 521.5 | 6.5 | 42.25 | 295.75 |
80 – 89 | 7 | 84.5 | 591.5 | 16.5 | 272.25 | 1905.75 |
90 – 99 | 4 | 94.5 | 378.0 | 26.5 | 702.25 | 2809 |
| 40 |
| 2720 |
|
| 10510 |
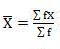
Mean = 2720/40 = 68
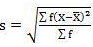
SD = √10510/40 = 16.20
Coefficient of Variation =  x 100%
x 100%
= 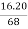 x 100%
x 100%
= 23.82 %
17. Below are the data of hours spent watching television by the 220 students. Calculate the Karl Pearson’s Co-efficient of Skewness .
Hours | No. Of students |
10 – 14 | 2 |
15 – 19 | 12 |
20 – 24 | 23 |
25 – 29 | 60 |
30 – 34 | 77 |
35 – 39 | 38 |
40 - 44 | 8 |
Solution:
Hours | No. Of students | x | Fx |
|
|
|
10 – 14 | 2 | 12 | 24 | -17.82 | 317.49 | 634.98 |
15 – 19 | 12 | 17 | 204 | -12.82 | 164.31 | 1971.67 |
20 – 24 | 23 | 22 | 506 | -7.82 | 61.12 | 1405.85 |
25 – 29 | 60 | 27 | 1620 | -2.82 | 7.94 | 476.53 |
30 – 34 | 77 | 32 | 2464 | 2.18 | 4.76 | 366.55 |
35 – 39 | 38 | 37 | 1406 | 7.18 | 51.58 | 1959.98 |
40 - 44 | 8 | 42 | 336 | 12.18 | 148.40 | 1187.17 |
| 220 |
| 6560 |
|
| 8002.73 |
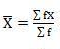
Mean = 6560/220 = 29.82

SD = √8002.73/220 = 6.03
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
Here modal class is 30 – 34 (Since the frequency is highest)
L1 = 30, L2 = 34, d1 = 17, d2 = 39
 Mode = 30 + (34 – 30) 17
Mode = 30 + (34 – 30) 17
17 + 39
Mode = 30 + 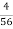 x 17
x 17
= 30 + 1.21
= 31.21
Therefore, Co-efficient of Skewness
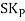 =
= 
= 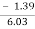
= - 0.23
18. Calculate Co-efficient of Skewness with the help of Bowley’s Method from the following data:
Sl. N o | Test scores |
1 | 17 |
2 | 17 |
3 | 26 |
4 | 27 |
5 | 30 |
6 | 30 |
7 | 31 |
8 | 37 |
Solution:
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (8 + 1) /4] th observation
Q1 = 2.25 th observation
Thus, 2.25 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 17 and 26
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 17 + 0.75 * (26 – 17) = 23.75
Second quartile(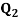 )
)
Q2= [2 * (8 + 1) /4] th observation
Q2 = 4.5th Observation
So, 4.5th observation lies between 4th and 5th value in ordered group, between frequency 27 and 30.
Hence Q2 = 4th observation + 0.50 * (5th observation – 6th observation)
Q2 = 27 + 0.50 * (30 – 27) = 28.5
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (8 + 1) /4] th observation
Q3 = 6.75 th observation
So, 6.75 th observation lies between the 6th and 7th value in the ordered group, between frequency 30 and 31
Third quartile (Q3) is calculated as
Q3 = 6th observation +0.25 * (7th observation – 6th observation)
Q3 = 30 + 0.25 * (31 – 30) = 30.25
Therefore, Bowley’s Coefficient of Skewness is calculated as under:

= 
= 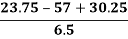 = - 0.461
= - 0.461









