UNIT 5

Isometric Projections

Question and answer

1. What do you mean by Isometric projection? Explain.

1. Isometric projection is a type of pictorial projection in which the three dimensions of a solid are not only shown in one view, but their actual sizes can be measured directly from it.

2. If a cube is placed on one of its corners on the ground with a solid diagonal perpendicular to the V.P., the front view is the isometric projection of the cube. The step-by-step construction is shown in fig. 1.

2.    

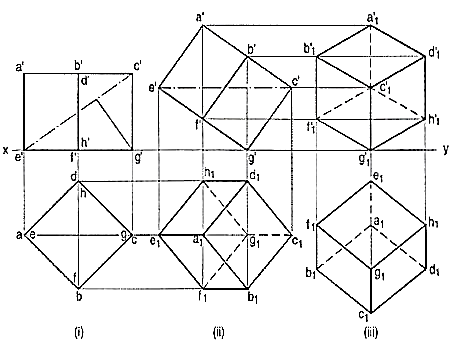
3.      Figure 1

4.     To draw the projections of a cube of 25 mm long edges resting on the ground on one of its corners with a solid diagonal perpendicular to the V.P., assume the cube to be resting on one of its faces on the ground with a solid diagonal parallel to the V.P.

5.     (i) Draw a square abed in the top view with its sides inclined at 45° to xy. The line ac representing the solid diagonals AG and CE is parallel to xy. Project the front view.

6.     (ii) Tilt the front view about the corner g' so that the line e' c' becomes parallel to xy. Project the second top view. The solid diagonal CE is now parallel to both the H.P. And the V.P.

7.     (iii) Reproduce the second top view so that the top view of the solid diagonal, viz. e1 c1 is perpendicular to xy. Project the required front view.

8.     Fig. 2 shows the front view of the cube in the above position, with the corners named in capital letters. Its careful study will show that

(a) All the faces of the cube are equally inclined to the V.P. And hence, they are seen as similar and equal rhombuses instead of squares.

(b) The three lines CB, CD and CG meeting at C and representing the three edges of the solid right-angle are also equally inclined to the V.P. And are therefore, equally foreshortened. They make equal angles of 120° with each other. The line CG being vertical, the other two lines CB and CD make 30° angle each, with the horizontal.

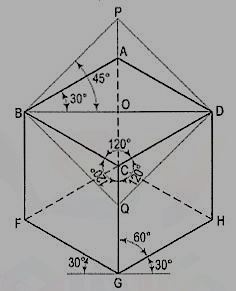
                                                               Figure 2

(c) All the other lines representing the edges of the cube are parallel to one or the other of the above three lines and are also equally foreshortened.

(d) The diagonal BO of the top face is parallel to the V.P. And hence, retains its true length.

This chapter deals with various topics of isometric projection as shown below:

1. Isometric axes, lines and planes

2. Isometric scale

3. Isometric drawing or isometric view

4. Isometric graph.

2. Write a short note on

a. Isometric axes

b. Isometric lines

C. Isometric planes

The three lines CB, CD and CG meeting at the point C and making 120° angles with each other are termed isometric axes. The lines parallel to these axes are called isometric lines. The planes representing the faces of the cube as well as other planes parallel to these planes are called isometric planes.

3. What do you understand by true and isometric scales?

As all the edges of the cube are equally foreshortened, the square faces are rhombuses. The rhombus ABCD (fig. 2) shows the isometric projection of the top square face of the cube in which BO is the true length of the diagonal.

Construct a square BQDP around BO as a diagonal. Then BP shows the true length of BA.

In triangle ABO,

In triangle PBO,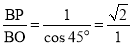 

The ratio,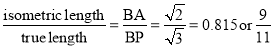

Thus, the isometric projection is reduced in the ratio,i.e. the isometric lengths are 0.815 of the true lengths.

Therefore, while drawing an isometric projection, it is necessary to convert true lengths into isometric lengths for measuring and marking the sizes. This is conveniently done by constructing and making use of an isometric scale as shown below.

a)     Draw a horizontal line BO of any length (fig. 3). At the end B, draw lines BA and BP, such that L OBA = 30° and L OBP = 45°. Mark divisions of true length on the line BP and from each division-point, draw verticals to BO meeting BA at respective points. The divisions thus obtained on BA give lengths on isometric scale.

Figure 3

(b) The same scale may also be drawn with divisions of natural scale on a horizontal line AB (fig. 4). At the ends A and B, draw lines AC and BC making 15° and 45° angles with AB respectively, and intersecting each other at C.

Figure 4

From division-points of true lengths on AB, draw lines parallel to BC and meeting AC at respective points. The divisions along AC give lengths to isometric scale.

The lines BO and AC (fig. 2) represent equal diagonals of a square face of the cube, but are not equally shortened in isometric projection. BO retains its true length, while AC is considerably shortened. Thus, it is seen that lines which are not parallel to the isometric axes are not reduced according to any fixed ratio. Such lines are called non-isometric lines. The measurements should, therefore, be made on isometric axes and isometric lines only. The non-isometric lines are drawn by locating positions of their ends on isometric planes and then joining them

4. Describe what do you mean by View and Isometric Projection?

If the foreshortening of the isometric lines in an isometric projection is disregarded and instead, the true lengths are marked, the view obtained [fig. 5(iii)] will be exactly of the same shape but larger in proportion (about 22.5%) than that obtained using the isometric scale [fig. 5(ii)]. Due to the ease in construction and the advantage of measuring the dimensions directly from the drawing, it has become a general practice to use the true scale instead of the isometric scale.

To avoid confusion, the view drawn with the true scale is called isometric drawing or isometric view, while that drawn with the use of isometric scale is called isometric projection.

Figure 5

Referring again to fig. 2, the axes BC and CD represent the sides of a right angle in horizontal position. Each of them together with the vertical axis CG, represents the right angle in vertical position. Hence, in isometric view of any rectangular solid resting on a face on the ground, each horizontal face will have its sides parallel to the two sloping axes; each vertical face will have its vertical sides parallel to the vertical axis and the other sides parallel to one of the sloping axes.

In other words, the vertical edges are shown by vertical lines, while the horizontal edges are represented by lines, making 30° angles with the horizontal. These lines are very conveniently drawn with the T-square and a 30°-60° set-square or drafter.

5. Write the process for Conversion of given Orthographic View into Isometric Projection?

An isometric graph as shown in fig. 6 facilitates the drawing of isometric view of an object. Students are advised to make practice for drawing of isometric view using such graphs.

Figure 6

6.  The front view of a square is given in fig. 7 (i). Draw its isometric view.

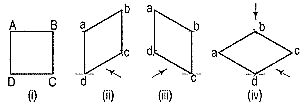
Figure 7

As the top view is a square, the surface of the square is horizontal. In isometric view, all the sides will be drawn inclined at 30° to the horizontal.

(i) From any point d, draw two lines da and dc inclined at 30° to the horizontal and making 120° angle between themselves.

(ii) Complete the rhombus abed which is the required isometric view.

Shows the front view of a circle whose surface is parallel to the V.P. Draw the isometric view of the circle.

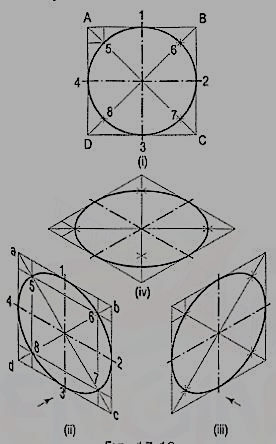
Figure 8

Oblique and Perspective projections:

Introduction:

Pictorial projections are used for presenting ideas which may be easily understood by all without technical training. They show several faces of an object in one view, as it appears to the eye approximately. Among the pictorial projections, Isometric Projections are the most common.

Oblique Projection:

Oblique Projection of an object may be obtained by projecting the object with parallel projections that are oblique to the picture plane

In oblique projection, the front face of the object appears in its true size and shape, as it is placed parallel to the picture plane. The receding lines representing the other two faces are usually drawn at 30°,45° or 60° to the horizontal, 45° being the most common practice.

As in the case of isometric projection, in oblique projection also, all lines that are parallel on the object appear parallel on the drawing and vertical lines on the object appear vertical.

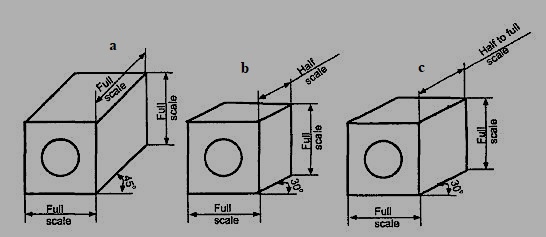
Figure 9

Classification of Oblique projection:

Oblique projections are classified as cavalier, cabinet and general, depending on the scale of measurement followed along the receding lines, as shown in Fig 10.1. The oblique projection shown in Fig 9.a presents a distorted appearance to the eye. To reduce the amount of distortion and to have a more realistic appearance, the length of the receding lines is reduced as shown, either in Fig. 9.b or as in Fig 9.c. If the receding lines are measured to the true size, the projection is known as cavalier projection. If they are reduced to one half of their true lengths, the projection is called cabinet projection. In general oblique, the measurement along the receding lines vary from half to full size.

Note: Oblique projection has the following advantages over isometric drawing:

1. Circular or irregular features on the front face appear in their true shape.

2. Distortion may be reduced by fore-shortening the measurement along the receding axis, and.

3. A greater choice is permitted in the selection of the position of the axes.

Methods of Drawing Oblique Projection:

The orthographic views of a V-block are shown in Fig. 10.a The stages in obtaining the oblique projection of the same are shown in Fig. 10.b.

Figure 10

1. After studying the views carefully, select the face that is either the most irregular one or the one with circular features if any. Make that face parallel to the picture plane to minimize distortion.

2. Draw the face to its true size and shape.

3. Draw the receding lines through all the visible comers of the front face.

4. Mark the length of the object along the receding lines and join these in the order.

5. Add other features if any on the top and side faces.

7. Write a short note on Perspective projection?

Perspective projection is a method of graphic representation of an object on a single plane called picture plane as seen by an observer stationed at a particular position relative to the object. As the object is placed behind the picture plane and the observer is stationed in front of the picture plane, visual rays from the eye of the observer to the object are cut by the picture plane. The visual rays locate the position of the object on the picture plane. This type of projection is called perspective projection. This is also known as scenographic projection or convergent projection.

Method of preparing a perspective view differs from the various other methods of projections discussed earlier. Here, the projectors or visual rays intersect at a common point known as station point. A perspective projection of a street with posts holding lights, as viewed by an observer from a station point, is shown in Fig. 15. The observer sees the object through a transparent vertical plane called picture plane as shown in Fig.l5(a). The view obtained on the picture plane is shown in Fig. 15(b). In this view, the true shape and size of the street will not be the object is viewed from a station point to which the visual rays converge. This method of projection is theoretically very similar to the optical system in photography and is extensively employed by architects to show the appearance of a building or by artist-draftsman in the preparation of illustrations of huge machinery or equipment.

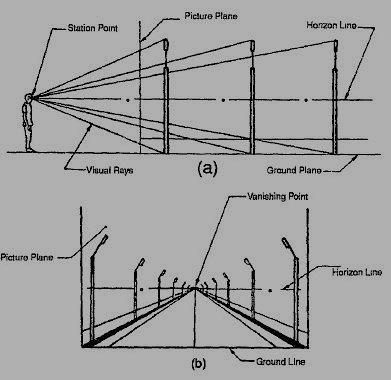
Figure 15

Nomenclature of Perspective Projection

The elements of perspective projection are shown in Fig. 16. The important terms used in the perspective projections are defined below.

1. Ground Plane (GP.): s is the plane on which the object is assumed to be placed.

2. Auxiliary Ground Plane (A.GP): This is any plane parallel to the ground plane (Not shown in Fig. 16)

3. Station Point (S.P.): This is the position of the observer's eye from where the object is viewed.

4. Picture Plane (P.P.): This is the transparent vertical plane positioned in between the station point and the object to be viewed. Perspective view is formed on this vertical plane.

5. Ground Line (GL.): This is the line of intersection of the picture plane with the ground plane.

6. Auxiliary Ground Line (A.GL.): This is the line of intersection of the picture plane with the auxiliary ground plane.

7. Horizon Plane (H.P.): This is the imaginary horizontal plane perpendicular to the picture plane and passing through the station point. This plane lies at the level of the observer.

8. Horizon Line (H.L.): This is the line of intersection of the horizon plane with the picture plane. This plane is parallel to the ground line.

9. Axis of Vision (A.V.): This is the line drawn perpendicular to the picture plane and passing through the station point. The axis of vision is also called the line of sight or perpendicular axis.

10. Centre of Vision (C. V.): This is the point through which the axis of vision pierces the picture plane. This is also the point of intersection of horizon line with the axis of vision.

11. Central Plane (C.P.): This is the imaginary plane perpendicular to both the ground plane and the picture plane. It passes through the centre of vision and the station point while containing the axis of vision.

12. Visual Rays (V.R.): These are imaginary lines or projectors joining the station point to the various points on the object. These rays converge to a point.

Figure 16

Classification of perspective projections

Perspective projections can be broadly classified into three categories.

I. Parallel perspective or single point perspective.

2. Angular perspective or two-point perspective.

3. Oblique perspective or three-point perspective.

8. Write the process of Isometric drawings of Prisms and Pyramids?

We have seen that the isometric view of a cube is determined from its orthographic view in a position. The three edges of the solid right-angle of the cube are shown by lines parallel to the three isometric axes. A square prism or a rectangular prism also has solid right-angles. Hence, lines for its edges are also drawn parallel to the three isometric axes.

While drawing the isometric view of any solid, the following important points should be carefully noted:

(i) The isometric view should be drawn according to the given views and in such a way that maximum possible details are visible.

(ii) At every point for the corner of a solid, at least three lines for the edges must converge. Of these, at least two must be for visible edges. Lines for the hidden edges need not be shown, but it is advisable to check up every corner so that no line for a visible edge is left out.

(iii) Two lines (for visible edges) will never cross each other.

9. Draw the isometric view of a square prism, side of the base 20 mm long and the axis 40 mm long, when its axis is (i) vertical and (ii) horizontal.

(i) When the axis is vertical, the ends of the prism will be horizontal. Draw the isometric view (the rhombus 1-2-3-4) of the top end [fig. 18 (i)]. Its sides will make 30°-angles with the horizontal. The length of the prism will be drawn in the third direction, i.e. vertical. Hence, from the corners of the rhombus, draw vertical lines 1-5, 2-6 and 3-7 of length equal to the length of the axis. The line 4-8 should not be drawn, as that edge will not be visible. Draw lines 5-6 and 6-7, thus completing the required isometric view. Lines 7-8 and 8-5 also should not be drawn. Beginning may also be made by drawing lines from the point 6 on the horizontal line and then proceeding upwards.

(ii) When the axis is horizontal, the ends will be vertical. The ends can be drawn in two ways as shown in fig. 18 (ii) and fig. 18 (iii). In each case, the length is shown in the direction of the third isometric axis.

Figure 18

10. Draw the isometric projection of a sphere resting centrally on the top of a square prism, the front view of which is shown in fig.

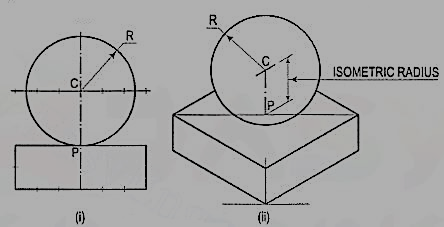
Figure 31

(i) Draw the isometric projection (using isometric scale) of the square prism and locate the centre P of its top surface .

(ii) Draw a vertical at P and mark a point C on it, such that PC = the isometric radius of the sphere.

(iii) With C as centre and radius equal to the radius of the sphere, draw a circle which will be the isometric projection of the sphere.