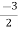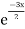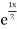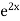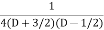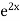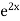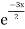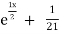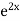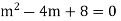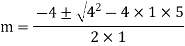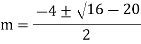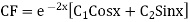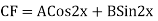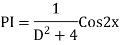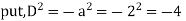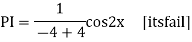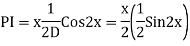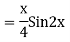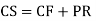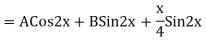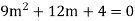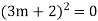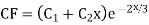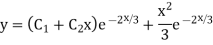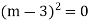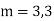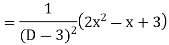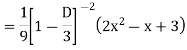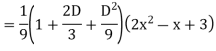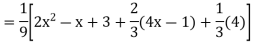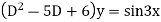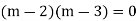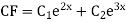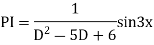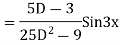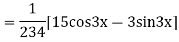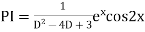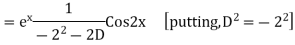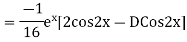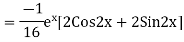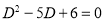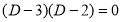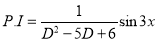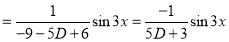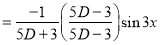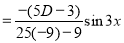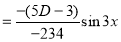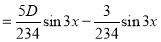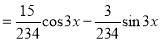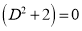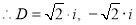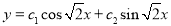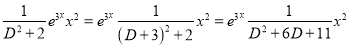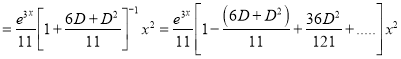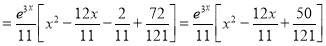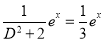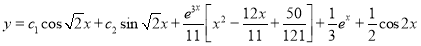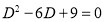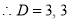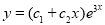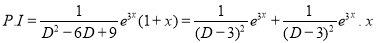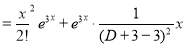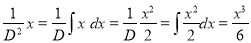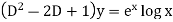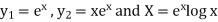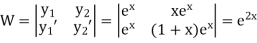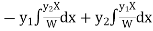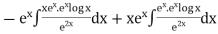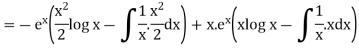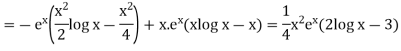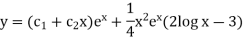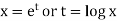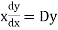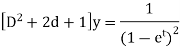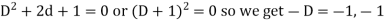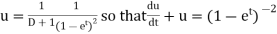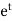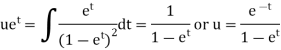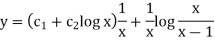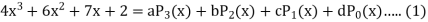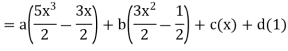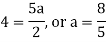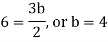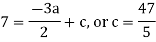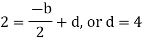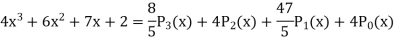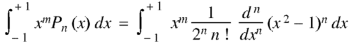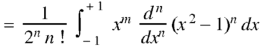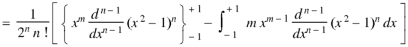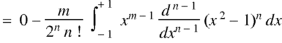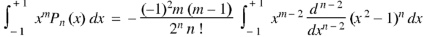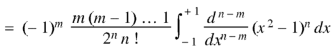S1) Auxiliary equation is 4m² +4m – 3 = 0

    We get,             (2m+3)(2m – 1) = 0

                               m =   ,

complementary function:  CF is  A+ B

now we will find particular integral,

                         P.I. = f(x)

=   .

=    .

=    .

=   . =   .

 General solution is y =  CF + PI

                                                    = A+ B  .

S2) Auxiliary equation are

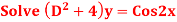
S3) Auxiliary equation are

S4) The AE is

Complete solution y= CF + PI

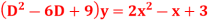
S5) The AE is

Complete solutio0n is y= CF + PI

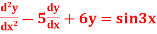
S6) Given equation in symbolic form is

Its Auxiliary equation is

Complete solution is y= CF + PI

S7)

S8)

Auxiliary equation

C.F is

    []

   The Complete Solution is  

S9)

The Auxiliary equation is   

  The C.F is

P.I

Now, 

   The Complete Solution is

S10)

The auxiliary equation is     

The C.F is

But

   The Complete Solution is

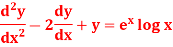
S11) This can be written as-

C.F.-

Auxiliary equation is-

So that the C.F. will be-

P.I.-

Here

Now

Thus PI = 

            = 

            = 

So that the complete solution is-

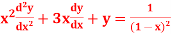
S12) On putting so that,

and

The given equation becomes-

Or it can be written as-

So that the auxiliary equation is-

C.F. =

Particular integral-

Where

It’s a Leibnitz’s linear equation having I.F.=

Its solution will be-

P.I. =

       =

So that the complete solution is-

S13)

By equating the coefficients of like powers of x, we get-

Put these values in equation (1), we get-

A14) By using Rodrigue formula for Legendre function.

On integrating by parts, we get-

Now integrating m – 2 times, we get-