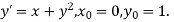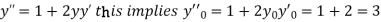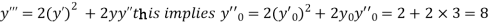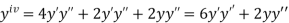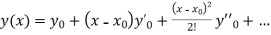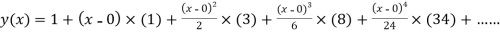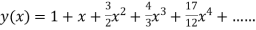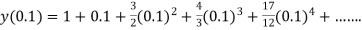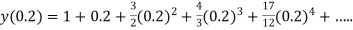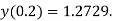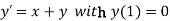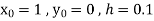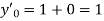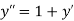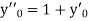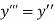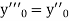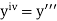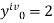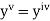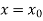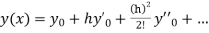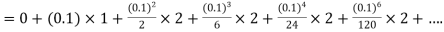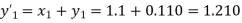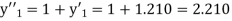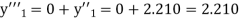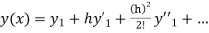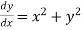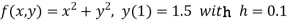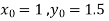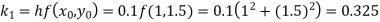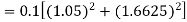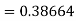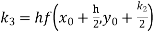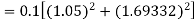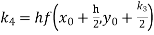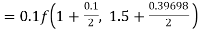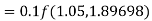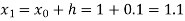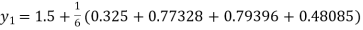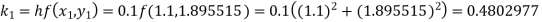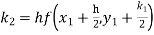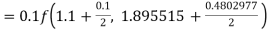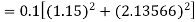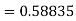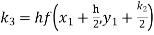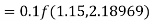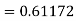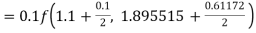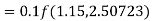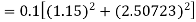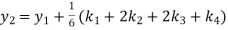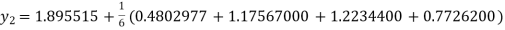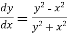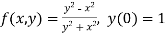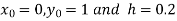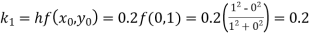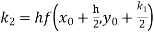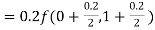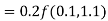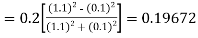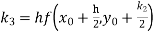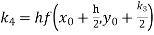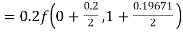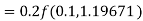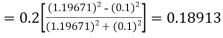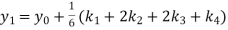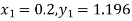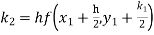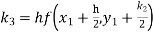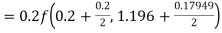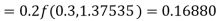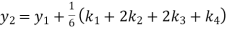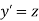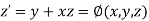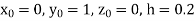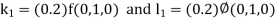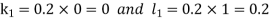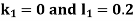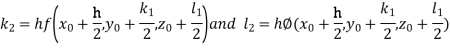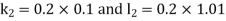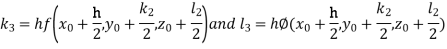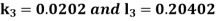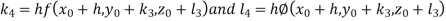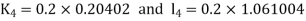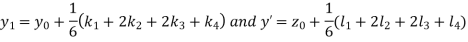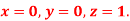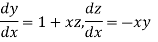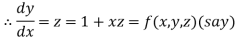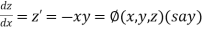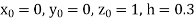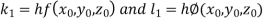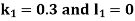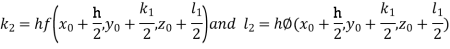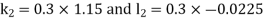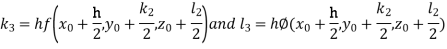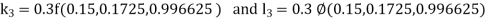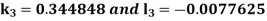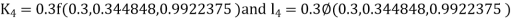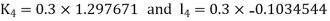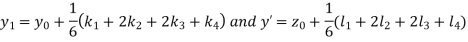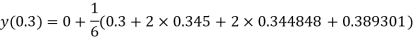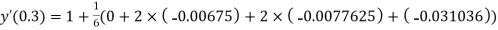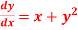 ,
, 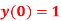 using Taylor’s series method and compute
using Taylor’s series method and compute 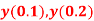 .
.S1) Here Differentiating, we get The Taylor’s series at At At |
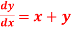 numerically, start from
numerically, start from 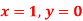 and carry to
and carry to  using Taylor’s series method.
using Taylor’s series method.S2) Here We have Differentiating, we get The Taylor’s series at Or Here The Taylor’s series |
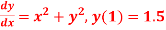
S3) Given equation Here Also By Runge Kutta formula for first interval Again A fourth order Runge Kutta formula: To find y at A fourth order Runge Kutta formula: |

S4) Given equation Here Also By Runge Kutta formula for first interval A fourth order Runge Kutta formula: Hence at x = 0.2 then y = 1.196 To find the value of y at x=0.4. In this case A fourth order Runge Kutta formula: Hence at x = 0.4 then y=1.37527 |
 to find
to find 
S5) Given second order differential equation is
Let Or
Or By RungeKutta Method we have
A fourth orderRungeKutta formula:
Q6) Solve the differential equations
Using four order RungeKutta method with initial conditions S6)Given differential equation are
Let
And Also By RungeKutta Method we have
A fourth order RungeKutta formula:
And
|