Unit 3
Partial Differentiation
Question and answer
- Decamper a positive number ‘a’ in to three parts, so their product is maximum
Solution:
Let x, y, z be the three parts of ‘a’ then we get.
 … (1)
… (1)
Here we have to maximize the product
i.e. 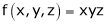
 By Lagrange’s undetermined multiplier, we get,
By Lagrange’s undetermined multiplier, we get,
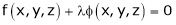
 … (2)
… (2)
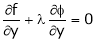 … (3)
… (3)
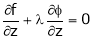 … (4)
… (4)
i.e.
 … (2)’
… (2)’
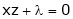 … (3)’
… (3)’
 … (4)
… (4)

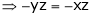
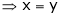
And 
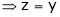

From (1)


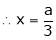
Thus  .
.
Hence their maximum product is 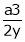 .
.
2. Find the point on plane  nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
Solution:
Let  be the point on sphere
be the point on sphere 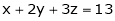 which is nearest to the point
which is nearest to the point  . Then shortest distance.
. Then shortest distance.
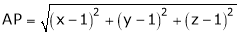
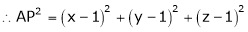
 Let
Let 
Under the condition 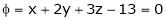 … (1)
… (1)
 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have
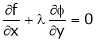
 … (2)
… (2)
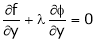
 … (3)
… (3)
i.e.  &
&

 … (4)
… (4)
From (2) we get 
From (3) we get 
From (4) we get 
 Equation (1) becomes
Equation (1) becomes
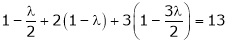
i.e. 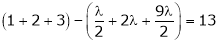

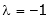

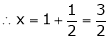
y = 2
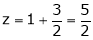
If  where x + y + z = 1.
where x + y + z = 1.
Prove that the stationary value of u is given by,

3. 
Consider 
Put 



 .
.
Thus degree of f(x, y) is 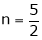
4. Find 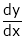 if
if 
