UNIT-5

Q:1 Find fourth root of

Solution: Convert to polar first:  r=

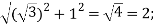
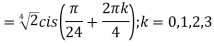
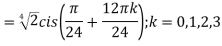
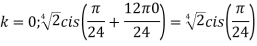
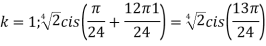
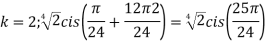
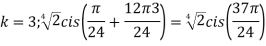
Q:2 Find the fifth root of 4-4i of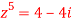

Solution: Convert 4-4i to polar: r==;()cis()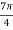

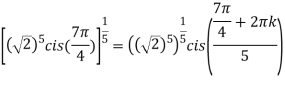
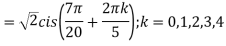
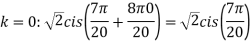
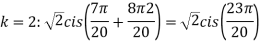
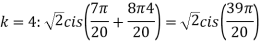
Q:3 Solve cosh2 x – sinh2 x

Solution:

Given: cosh2 x – sinh2 x

We know that

Sinh x = [ex– e-x]/2

Cosh x = [ex + e-x]/2

Cosh2 x – sinh2 x = [ [ex + e-x]/2 ]2 – [ [ex – e-x]/2 ]2

Cosh2 x – sinh2 x = (4ex-x) /4

Cosh2 x – sinh2 x = (4e0) /4

Cosh2 x – sinh2 x = 4(1) /4 = 1

Therefore, cosh2 x – sinh2 x = 1

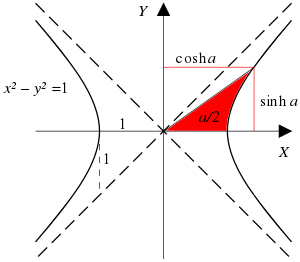
A ray through the unit hyperbola x 2   −   y 2   =   1 {\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1} in the point ( cosh a , sinh a ) {\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)} , where a {\displaystyle \scriptstyle a} is twice the area between the ray, the hyperbola, and the x {\displaystyle \scriptstyle x} -axis

Q:4 Find the inverse of the function f(x) = ln(x – 2)

Solution:

First, replace f(x) with y

So, y = ln(x – 2)

Replace the equation in exponential way , x – 2 = ey

Now, solving for x,

x = 2 + ey

Now, replace x with y and thus, f-1(x) = y = 2 + ey

Q:5 To solve an equation: f(x) = 2x + 3, at x = 4

Solution:

We have,

f(4) = 2 × 4 + 3

f(4) = 11

Now, let’s apply for reverse on 11.

f-1(11) = (11 – 3) / 2

f-1(11) = 4

Magically we get 4 again.

Therefore, f(f(4)) = f(4)

So, when we apply function f and its reverse f-1 gives the original value back again, i.e, f-1(f(x)) = x.

Q:6 Prove that function is analytic function.

Solution. Real and Imaginary parts of are

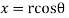
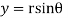
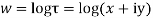
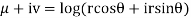
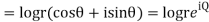
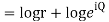
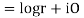
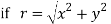
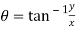
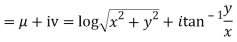
If,

On differentiating u,v we get

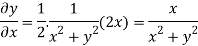
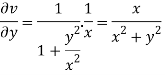
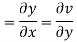
Again differentiating

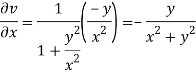
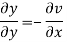
Q:7 Determine P such that the function analytic

Solution: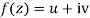     

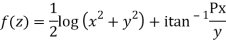
Hence  

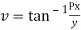
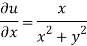
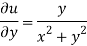
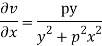
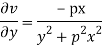
f(z) is analytic Cauchy Riemann should be satisfied that is

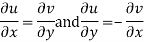
And                            

P=-1

Q:8 Problem: simplify 16 i+10i (3-i)

Solution:

Given,

16i +10i (3-i)

=16i+10i (3i) +10 i(-i)

=16i+30i-10i2

=46i-10(-1)

=46i+10

Here real part is 10 and imaginary part is 46

Q:9 Problem: express the following into a+ib form

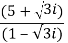
Solution:

Given.,   

 
z  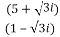 =        = = + i

Modulus, = = =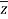 

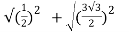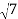
Conjugate = (  -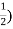