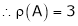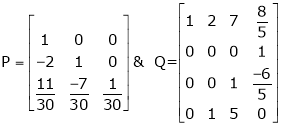Unit 1
Unit 1
Matrices
Question and answer
- Reduce the following matrix to the normal form of Hence find it’s rank,

Solution:
We have,





Apply 

 The rank of A = 1
The rank of A = 1
2. Find the rank of the matrix

Solution:
We have,

Apply R12











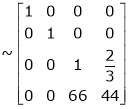





 The rank of A = 3
The rank of A = 3
3. Find the rank of the following matrices by reducing it to the normal form.
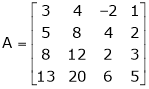
Solution:

Apply C14















4. Reduce the following matrix to the normal form of Hence find it’s rank,

Solution:
We have,




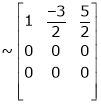
Apply 


 The rank of A = 1
The rank of A = 1
5. If  Find Two
Find Two
Matrices P and Q such that PAQ is in normal form.
Solution:
Here A is a square matrix of order 3 x 3. Hence, we write,
A = I3 A.I3
i.e. 



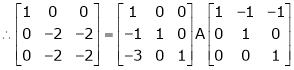






i.e. 


6. Are the vectors  ,
,  ,
,  linearly dependent. If so, express x1 as a linear combination of the others.
linearly dependent. If so, express x1 as a linear combination of the others.
Solution:
Consider a vector equation,
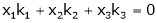
i.e. 




Which can be written in matrix form as,

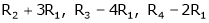





Here 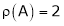 & no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
& no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,


Put 
 and
and


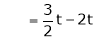
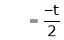
Thus 
i.e. 
i.e. 


Since F11 k2, k3 not all zero. Hence  are linearly dependent.
are linearly dependent.
7. Determine the eigen values of the eigenvector of the matrix.

Solution:
Consider the characteristic equation as 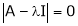
i.e. 
i.e. 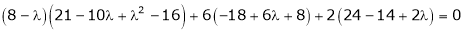



i.e. 
Which is the required characteristic equation.

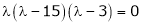
 are the required eigenvalues.
are the required eigenvalues.
Now consider the equation
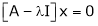 … (1)
… (1)
Case I:
If  Equation (1)becomes
Equation (1)becomes

R1 + R2







Thus 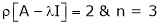
 independent variable.
independent variable.
Now rewrite the equation as,


Put x3 = t
 &
&



Thus  .
.
Is the eigenvector corresponding to  .
.
Case II:
If  equation (1) becomes,
equation (1) becomes,







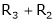

Here 
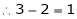 independent variables
independent variables
Now rewrite the equations as,
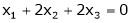

Put 
 &
&



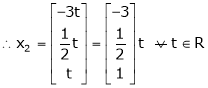 .
.
Is the eigenvector corresponding to  .
.
Case III:
If 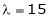 equation (1) becomes,
equation (1) becomes,






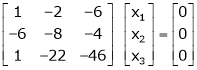




Here the rank of 
 independent variable.
independent variable.
Now rewrite the equations as,


Put 

Thus 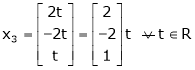 .
.
Is the eigenvector for  .
.
8. Find the eigenvalues of an eigenvector for the matrix.

Solution:
Consider the characteristic equation as 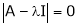
i.e. 



i.e. 


 are the required eigenvalues.
are the required eigenvalues.
Now consider the equation
 … (1)
… (1)
Case I:
 Equation (1) becomes,
Equation (1) becomes,

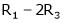

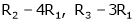
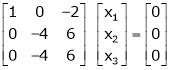

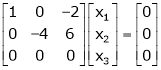
Thus  and n = 3
and n = 3
 3 – 2 = 1 independent variables.
3 – 2 = 1 independent variables.
Now rewrite the equations as,


Put 
 ,
, 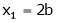

i.e. the eigenvector for 
Case II:
If  equation (1) becomes,
equation (1) becomes,





Thus 
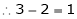
Independent variables.
Now rewrite the equations as,


Put 






Is the eigenvector for 
Now
Case II:-
If  equation (1) gives,
equation (1) gives,

R1 – R2





Thus 
 independent variables
independent variables
Now 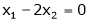

Put 
Thus

Is the eigenvector for  .
.
9. Find a non – singular matrices p and Q such that P A Q is in a normal form where

Solution:
Here A is a matrix of order 3 x 4. Hence, we write A as,

i.e.
















i.e. 


Unit 1
Matrices
Question and answer
- Reduce the following matrix to the normal form of Hence find it’s rank,

Solution:
We have,





Apply 
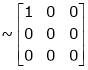

 The rank of A = 1
The rank of A = 1
2. Find the rank of the matrix

Solution:
We have,

Apply R12


















 The rank of A = 3
The rank of A = 3
3. Find the rank of the following matrices by reducing it to the normal form.

Solution:

Apply C14



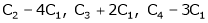





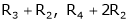




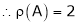
4. Reduce the following matrix to the normal form of Hence find it’s rank,
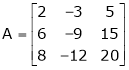
Solution:
We have,





Apply 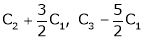
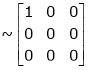

 The rank of A = 1
The rank of A = 1
5. If  Find Two
Find Two
Matrices P and Q such that PAQ is in normal form.
Solution:
Here A is a square matrix of order 3 x 3. Hence, we write,
A = I3 A.I3
i.e. 






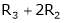


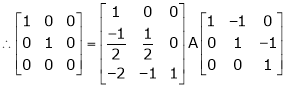
i.e. 


6. Are the vectors  ,
,  ,
,  linearly dependent. If so, express x1 as a linear combination of the others.
linearly dependent. If so, express x1 as a linear combination of the others.
Solution:
Consider a vector equation,
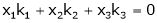
i.e. 




Which can be written in matrix form as,





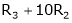

Here  & no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
& no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,

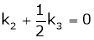
Put 
 and
and




Thus 
i.e. 
i.e. 
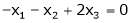

Since F11 k2, k3 not all zero. Hence 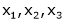 are linearly dependent.
are linearly dependent.
7. Determine the eigen values of the eigenvector of the matrix.

Solution:
Consider the characteristic equation as 
i.e. 
i.e. 

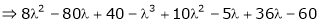

i.e. 
Which is the required characteristic equation.


 are the required eigenvalues.
are the required eigenvalues.
Now consider the equation
 … (1)
… (1)
Case I:
If  Equation (1)becomes
Equation (1)becomes

R1 + R2
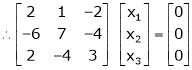






Thus 
 independent variable.
independent variable.
Now rewrite the equation as,

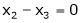
Put x3 = t
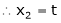 &
&



Thus  .
.
Is the eigenvector corresponding to  .
.
Case II:
If  equation (1) becomes,
equation (1) becomes,





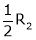



Here 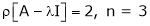
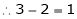 independent variables
independent variables
Now rewrite the equations as,


Put 
 &
&



 .
.
Is the eigenvector corresponding to  .
.
Case III:
If 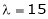 equation (1) becomes,
equation (1) becomes,
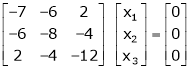










Here the rank of 
 independent variable.
independent variable.
Now rewrite the equations as,

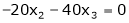
Put 
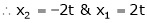
Thus  .
.
Is the eigenvector for  .
.
8. Find the eigenvalues of an eigenvector for the matrix.

Solution:
Consider the characteristic equation as 
i.e. 



i.e. 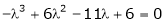


 are the required eigenvalues.
are the required eigenvalues.
Now consider the equation
 … (1)
… (1)
Case I:
 Equation (1) becomes,
Equation (1) becomes,

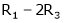

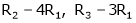



Thus  and n = 3
and n = 3
 3 – 2 = 1 independent variables.
3 – 2 = 1 independent variables.
Now rewrite the equations as,
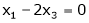

Put 
 ,
, 

i.e. the eigenvector for 
Case II:
If  equation (1) becomes,
equation (1) becomes,

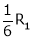



Thus 

Independent variables.
Now rewrite the equations as,


Put 

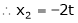




Is the eigenvector for 
Now
Case II:-
If  equation (1) gives,
equation (1) gives,

R1 – R2





Thus 
 independent variables
independent variables
Now 

Put 
Thus
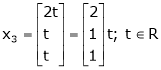
Is the eigenvector for  .
.
9. Find a non – singular matrices p and Q such that P A Q is in a normal form where

Solution:
Here A is a matrix of order 3 x 4. Hence, we write A as,

i.e.
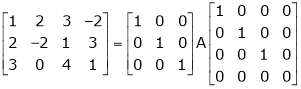


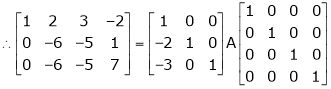












i.e.