Unit 2
Unit 2
Differential and Integral Calculus
Question and answer
- Verify Rolle’s theorem for the function f(x) = x2 for
Solution:
Here f(x) = x2; 
i) Since f(x) is algebraic polynomial which is continuous in [-1, 1]
Ii) Consider f(x) = x2
Diff. w.r.t. x we get
f'(x) = 2x
Clearly f’(x) exists in (-1, 1) and does not becomes infinite.
Iii) Clearly
f(-1) = (-1)2 = 1
f(1) = (1)2 = 1
f(-1) = f(1).
Hence by Rolle’s theorem, there exist 
such that
f’(c) = 0
i.e. 2c = 0
c = 0
Thus 
such that
f'(c) = 0
Hence Rolle’s Theorem is verified.
2. Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in 
Solution:
Here f(x) = ex(sin x – cos x); 
i) Ex is an exponential function continuous for every 
also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in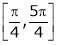 
and Hence ex(sin x – cos x) is continuous in 
.
Ii) Consider
f(x) = ex(sin x – cos x)
Diff. w.r.t. x we get
f’(x) = ex(cos x + sin x) + ex(sin x + cos x)
= ex[2sin x]
Clearly f’(x) is exist for each 
& f’(x) is not infinite.
Hence f(x) is differentiable in 
.
Iii) Consider
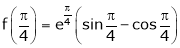
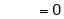
Also,
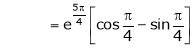
Thus 
Hence all the conditions of Rolle’s theorem are satisfied, so there exist 
such, that
i.e. 
i.e. sin c = 0
But
Hence Rolle’s theorem is verified.
3. Verify whether Rolle’s theorem is applicable or not for
Solution:
Here f(x) = x2; 
i) X2 is an algebraic polynomial hence it is continuous in [2, 3]
Ii) Consider
F’(x) exists for each 
Iii) Consider
Thus 
.
Thus all conditions of Rolle’s theorem are not satisfied Hence Rolle’s theorem is not applicable for f(x) = x2 in [2, 3]
4. Verify the Lagrange’s mean value theorem for
Solution:
Here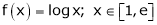 
i) Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]
Ii) Consider f(x) = log x.
Diff. w.r.t. x we get,
Clearly f’(x) exists for each value of 
& is finite.
Hence all conditions of LMVT are satisfied Hence at least 
Such that
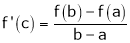
i.e.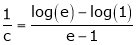 
i.e. 
i.e. 
i.e.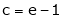 
Since e = 2.7183
Clearly c = 1.7183 
Hence LMVT is verified.
5. Verify mean value theorem for f(x) = tan-1x in [0, 1]
Solution:
Here 
; 
i) Clearly 
is an inverse trigonometric function and hence it is continuous in [0, 1]
Ii) Consider 
Diff. w.r.t. x we get,
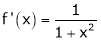
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite
Hence all conditions of LMVT are satisfied, Thus there exist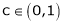 
Such that
i.e. 
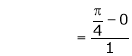
i.e. 
i.e.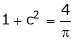 
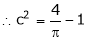
i.e. 
Clearly 
Hence LMVT is verified.
6. Verify Cauchy mean value theorems for 
&
in 
Solution:
Let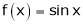 
&
; 
i) Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in 
Ii) Since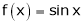 
&
Diff. w.r.t. x we get,
&
Clearly both f’(x) and g’(x) exist & finite in 
. Hence f(x) and g(x) is derivable in 
and
Iii) 
Hence by Cauchy mean value theorem, there exist at least 
such that
i.e. 
i.e. 1 = cot c
i.e. 
Clearly 
Hence Cauchy mean value theorem is verified.
7. Expansion of (1 + x)m
Proof:-
Let f(x) = (1 + x)m
By Maclaurin’s series.
… (1)
By equation (1) we get,
Note that in above expansion if we replace m = -1 then we get,
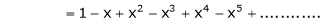
Now replace x by -x in above we get,
8. Expand 
upto x6
Solution:
Here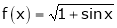 
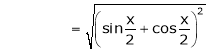
Now we know that
… (1)
… (2)
Adding (1) and (2) we get
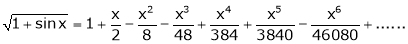
9. Using Taylors series method expand
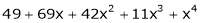in powers of (x + 2)
Solution:
Here 
a = -2
By Taylors series,
… (1)
Since
,
, …..
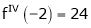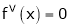Thus equation (1) becomes
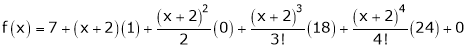
10. Expand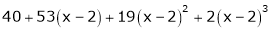 
in ascending powers of x.
Solution:
Here
i.e. 
Here h = -2
By Taylors series,
… (1)
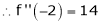
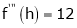
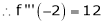
equation (1) becomes,
Thus
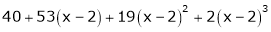
Unit 2
Differential and Integral Calculus
Question and answer
- Verify Rolle’s theorem for the function f(x) = x2 for
Solution:
Here f(x) = x2; 
i) Since f(x) is algebraic polynomial which is continuous in [-1, 1]
Ii) Consider f(x) = x2
Diff. w.r.t. x we get
f'(x) = 2x
Clearly f’(x) exists in (-1, 1) and does not becomes infinite.
Iii) Clearly
f(-1) = (-1)2 = 1
f(1) = (1)2 = 1
f(-1) = f(1).
Hence by Rolle’s theorem, there exist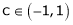 
such that
f’(c) = 0
i.e. 2c = 0
c = 0
Thus 
such that
f'(c) = 0
Hence Rolle’s Theorem is verified.
2. Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in 
Solution:
Here f(x) = ex(sin x – cos x); 
i) Ex is an exponential function continuous for every 
also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in 
and Hence ex(sin x – cos x) is continuous in 
.
Ii) Consider
f(x) = ex(sin x – cos x)
Diff. w.r.t. x we get
f’(x) = ex(cos x + sin x) + ex(sin x + cos x)
= ex[2sin x]
Clearly f’(x) is exist for each 
& f’(x) is not infinite.
Hence f(x) is differentiable in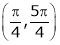 
.
Iii) Consider
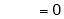
Also,
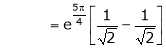
Thus 
Hence all the conditions of Rolle’s theorem are satisfied, so there exist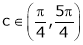 
such, that
i.e. 
i.e. sin c = 0
But
Hence Rolle’s theorem is verified.
3. Verify whether Rolle’s theorem is applicable or not for
Solution:
Here f(x) = x2; 
i) X2 is an algebraic polynomial hence it is continuous in [2, 3]
Ii) Consider
F’(x) exists for each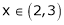 
Iii) Consider
Thus 
.
Thus all conditions of Rolle’s theorem are not satisfied Hence Rolle’s theorem is not applicable for f(x) = x2 in [2, 3]
4. Verify the Lagrange’s mean value theorem for
Solution:
Here 
i) Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]
Ii) Consider f(x) = log x.
Diff. w.r.t. x we get,
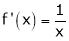
Clearly f’(x) exists for each value of 
& is finite.
Hence all conditions of LMVT are satisfied Hence at least 
Such that
i.e. 
i.e. 
i.e. 
i.e. 
Since e = 2.7183
Clearly c = 1.7183 
Hence LMVT is verified.
5. Verify mean value theorem for f(x) = tan-1x in [0, 1]
Solution:
Here 
; 
i) Clearly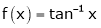 
is an inverse trigonometric function and hence it is continuous in [0, 1]
Ii) Consider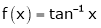 
Diff. w.r.t. x we get,
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite
Hence all conditions of LMVT are satisfied, Thus there exist 
Such that
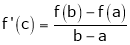
i.e. 
i.e. 
i.e. 
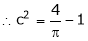
i.e. 
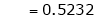
Clearly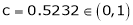 
Hence LMVT is verified.
6. Verify Cauchy mean value theorems for 
&
in 
Solution:
Let 
&
; 
i) Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in 
Ii) Since 
&
Diff. w.r.t. x we get,
&
Clearly both f’(x) and g’(x) exist & finite in 
. Hence f(x) and g(x) is derivable in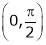 
and
Iii) 
Hence by Cauchy mean value theorem, there exist at least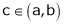 
such that
i.e. 
i.e. 1 = cot c
i.e.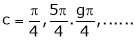 
Clearly 
Hence Cauchy mean value theorem is verified.
7. Expansion of (1 + x)m
Proof:-
Let f(x) = (1 + x)m
By Maclaurin’s series.
… (1)
By equation (1) we get,
Note that in above expansion if we replace m = -1 then we get,
Now replace x by -x in above we get,
8. Expand 
upto x6
Solution:
Here 
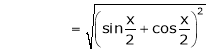
Now we know that
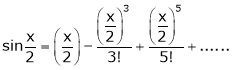… (1)
… (2)
Adding (1) and (2) we get
9. Using Taylors series method expand
in powers of (x + 2)
Solution:
Here 
a = -2
By Taylors series,
… (1)
Since
,
, …..
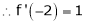
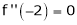
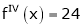
Thus equation (1) becomes
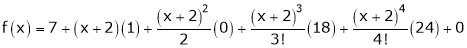
10. Expand 
in ascending powers of x.
Solution:
Here
i.e. 
Here h = -2
By Taylors series,
… (1)
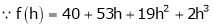
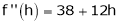
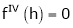
equation (1) becomes,
Thus
