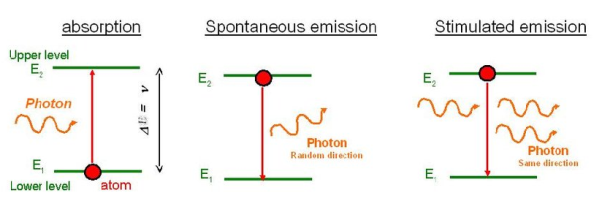
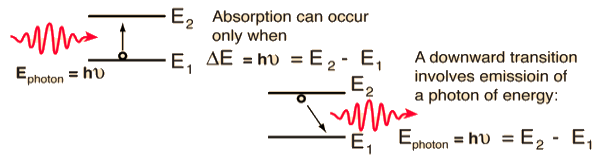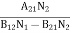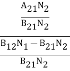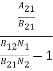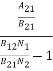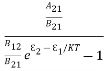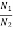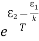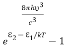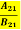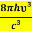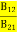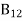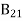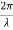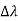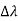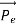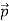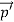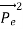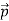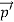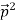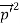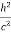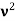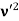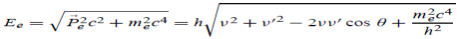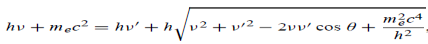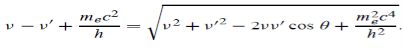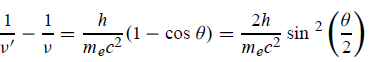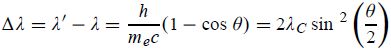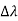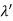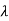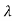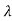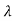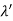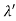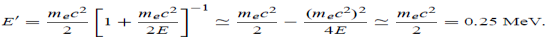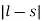Q1) Differentiate between spontaneous and stimulated emissions. A1)
Q2) Discuss Einstein’s theory of interaction of electromagnetic radiation with matter? A2) Let us discuss Einstein’s theory of interaction of electromagnetic radiation with matter. He proposed that electromagnetic radiation interacts with matter in following three steps.
Stimulated Absorption:
Let E1 and E2 be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation form ground state E1 to excited state E2. This process is called stimulated absorption. Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.
Stimulated absorption rate ∝ Number of atoms in the ground state ∝ Density of photons Spontaneous emission
Spontaneous Emission:
Let E1 and E2 be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation form ground stateE1 to excited state E2. The excited atom does not stay in a long time in the excited state. The excited atom gets de-excitation after its life time by emitting a photon of energy hν= E1− E2. This process is called spontaneous emission. Also Spontaneous means by its own. Here excited atom comes to ground state by its own so it is named as spontaneous emission.
The spontaneous emission rate depends up on the number of atoms present in the excited state.
Spontaneous emission ∝ rate number of atoms in the excited state
Stimulated Emission: This phenomena is responsible for producing laser light. Let E1and E2 be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation form ground stateE1 to excited state E2. Let, a photon of energy hν= E1− E2 interacts with the excited atom with in their life time; the atom gets de-excitation to ground state by emitting of another photon. These photons have same phase and it follows coherence. This phenomenon is called stimulated emission.
Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.
Stimulated emission rate ∝ number of atoms in the excited state ∝ Density of photons
Q3) Calculate the wavelength of radiation emitted by an LED made up of a semiconducting material with band gap energy 2.8eV. A3) E = hc/ʎ
Q4) Calculate the number of photons, from green light of mercury (ʎ = 4961 Å), required to do one joule of work. A4) E = hc/ʎ
Q5) Derive Einstein’s coefficient A and B ? A5) The distribution of atoms in the two energy levels will change by absorption or emission of radiation. Einstein introduced three empirical coefficients to quantify the change of population of the two levels. Let N1 be the number of atoms per unit volume with energy E1 and N2 be the number of atoms per unit volume with energy E2. Let ‘n’ be the number of photons per unit volume at frequency ‘υ’ such that hυ= E1− E2. Then, the energy density of photons ρ(υ) = nhυ
When these photons interact with atoms, both upward (absorption) and downward (emission) transition occurs. At the equilibrium the upward transitions must be equal downward transitions. Upward Transition Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons. We have seen above that Stimulated absorption rate ∝ N1 i.e. Number of atoms in the ground state ∝ ρ(υ) i.e. Density of photons spontaneous emission
Stimulated absorption rate = B12N1ρ(υ) ………(1) Where B12 is the Einstein coefficient of stimulated absorption. Downward transition The spontaneous emission rate depends up on the number of atoms present in the excited state. Spontaneous emission rate ∝ N2 i.e. number of atoms in the excited state Spontaneous emission rate = A21N2 ………(2) Where A21 is the Einstein coefficient of spontaneous emission. Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons. Stimulated emission rate ∝ N2 i.e. number of atoms in the excited state ∝ ρ(υ) i.e. Density of photons Stimulated emission rate = B21N2ρ(υ) ………(3) If the system is in equilibrium the upward transitions must be equal downward transitions. upward transitions = downward transitions B12N1ρ(υ) = A21N2 + B21N2ρ(υ) ………(4) B12N1ρ(υ) - B21N2ρ(υ) = A21N2 (B12N1- B21N2) ρ(υ) = A21N2 ρ(υ) = Divide with B21N2 in numerator and denominator in right side of the above equation, ρ(υ) = ρ(υ) = We know from Maxwell Boltzmann distribution law
And also from Planck’s law, the radiation density ρ(υ) = Comparing the two equations (7) and (9)
The above relations referred to as Einstein relations. From the above equation for non degenerate energy levels the stimulated emission rate is equal to the stimulated absorption rate at the equilibrium condition.
Q6) What is the relationship between B21 and B12? A6) C is the correct answer.
Q7) Discuss construction, working and application of gas Laser?
Or
Discuss construction, working and application of He-Ne Laser?
Or Discuss four level laser ?
A7) He-Ne Laser The first He-Ne gas laser was fabricated in 1961 by Ali Javan, Bennett and Herriott at Bell Telephone Laboratories. others. Helium-Neon laser is a type of gas laser in which a mixture of helium and neon gas is used as a gain medium. Helium-Neon laser is also known as He-Ne laser. The helium-neon laser was the first continuous wave laser ever constructed. The helium-neon laser operates at a wavelength of 632.8 nanometres (nm), in the red portion of the visible spectrum. Ruby laser is a pulse laser, even it have high intense output. For continuous laser beam gas lasers are used. Using gas lasers, we can achieve highly coherence, high directionality and high monochromacity beam. The output power of the gas laser is generally in few milliwatts. Construction The helium-neon laser consists of three essential components:
Pump source The gain medium of a helium-neon laser is made up of the mixture of helium and neon gas contained in a glass tube at low pressure. In He-Ne gas laser, the He and Ne gases are taken in the ratio 10:1 in the discharge tube.
Gain medium In He-Ne laser 80cm length and 1cm diameter discharge is generally used. The out power of these lasers depends on the length of the discharge tube and pressure of the gas mixture. Therefore, in order to achieve population inversion, we need to pump electrons from lower energy state of the helium. In He-Ne laser, neon atoms are the active centres and have energy levels suitable for laser transitions while helium atoms help in exciting neon atoms.
Resonating cavity Two reflecting mirrors are fixed on either ends of the discharge tube, in that, one is partially reflecting and the other is fully reflecting. The fully silvered mirror will completely reflect the light whereas the partially silvered mirror will reflect most part of the light but allows some part of the light to produce the laser beam.
Working
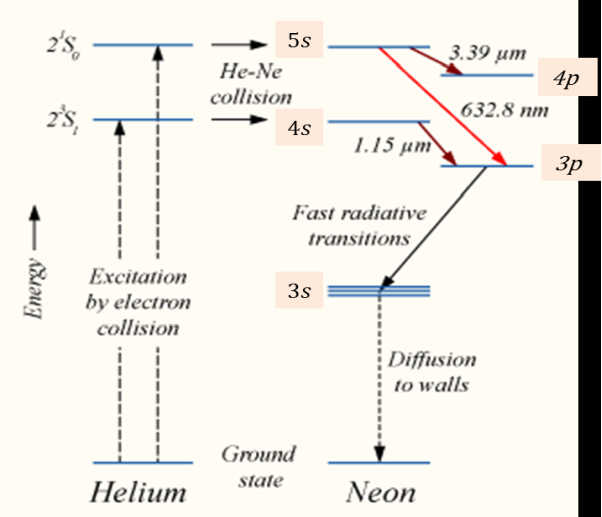
When the electric discharge is passing through the gas mixture, the electrons accelerated towards the positive electrode. During their passage, they collide with He atoms and excite them into higher levels. 23s1 and 21s0 form ground state of He atom. In higher levels 23s1 and 21s0, the life time of He atoms is more. So there is a maximum possibility of energy transfer between He and Ne atoms through atomic collisions. When He atoms present in the levels 23s1 and 21s0 collide with Ne atoms present ground state, the Ne atoms gets excitation into higher levels 4s and 5s.
Due to the continuous excitation of Ne atoms, we can achieve the population inversion between the higher levels 4s and 5s and lower levels 3p and 4p. The various transitions 5s to 4p, 4s to 3p and 5s to 3p leads to the emission of wavelengths 3.93μm, 1.51μm and 6328 Å or 632.8μm.
The first two corresponding to the infrared region while the last wavelength is corresponding to the visible region. The Ne atoms present in the 4s level are de-excited into 3s level, by spontaneously emitting a photon of around wavelength 6000 Å. When a narrow discharge tube is used, the Ne atoms present in the level 3s collide with the walls of the tube and get de-excited to ground state energy level.
Advantages of helium-neon laser
Disadvantages of helium-neon laser
Applications of helium-neon lasers
Q8) Discuss Properties Of Laser Beams?
A8) The laser light exhibits some peculiar properties than compare with the convectional light. Those are 1. Highly monochromatic 2. Highly coherence 3. Highly directionality 4. Highly intense 5. Laser Speckles
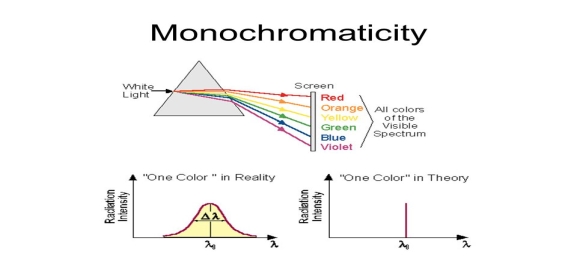
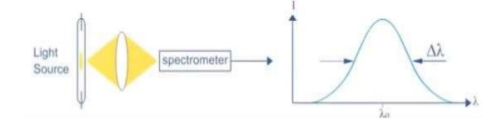
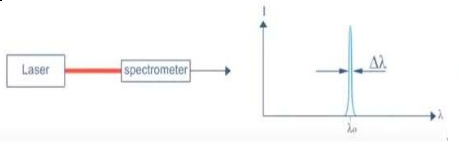
1. Highly monochromatic Monochromatic light means a light containing a single colour or wavelength. The photons emitted from ordinary light sources have different energies, frequencies, wavelengths, or colours. Ordinary light is a mixture of waves having different frequencies or wavelengths. The light waves of laser have single wavelength or colour.
Therefore, laser light covers a very narrow range of frequencies or wavelengths.
Hence The laser light is more monochromatic than that of a convectional light source. This may be due to the stimulated characteristic of laser light. The band width of convectional monochromatic light source is 1000 Å. But the band width of ordinary light source is 10 Å. For high sensitive laser source is 10-8 Å.
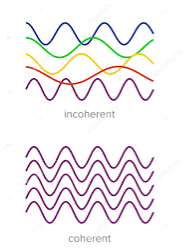
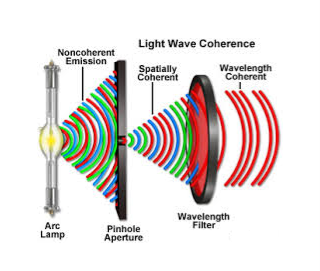
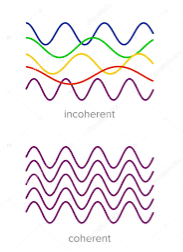
2. Highly coherence Definition:- A predictable correlation of the amplitude and phase at any one point with other point is called coherence.
Two waves are said to be coherent, the waves must have
In case of convectional light, the property of coherence exhibits between a source and its virtual source where as in case of laser the property coherence exists between any two of more light waves.
There are two types of coherence i) Temporal coherence ii) Spatial coherence
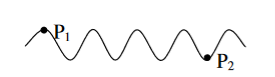
Temporal coherence (or longitudinal coherence):- The predictable correlation of amplitude and phase at one point on the wave train w .r. t another point on the same wave train, then the wave is said to be temporal coherence
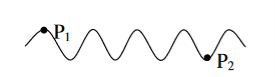
To understand this, let us consider two points P1 and P2 on the same wave train, which is continuous as in shown in figure.
Suppose the phase and amplitude at any one point is known, then we can easily calculate the amplitude and phase for any other point on the same wave train by using the wave equation y= a sin ( Where ‘a’ is the amplitude of the wave and ‘x’ is the displacement of the wave at any instant of time‘t’.
Spatial coherence (or transverse coherence) The predictable correlation of amplitude and phase at one point on the wave train w. r .t another point on a second wave, then the waves are said to be spatial coherence (or transverse coherence)
3. Highly directionality
The light ray coming ordinary light source travels in all directions, but laser light travels in single direction. For example the light emitted from torch light spreads 1km distance it spreads 1 km distance. But the laser light spreads a few centimetres distance even it travels lacks of kilometre distance. The directionality of laser beam is expressed in terms of divergence
∆θ = Where r1 and r2 are the radii of laser bam spots at distances of D1 and D2 respectively from laser source.
4. Highly Intense or Brightness We know that the intensity of a wave is the energy per unit time flowing through a unit normal area. Laser light is highly intense than the convectional light. An one mill watt He-Ne laser is highly intense than the sun intensity. This is because of coherence and directionality of laser. Suppose when two photons each of amplitude a are in phase with other, then young’s principle of superposition, the resultant amplitude of two photons is 2a and the intensity is 4a2. Since in laser many number of photons are in phase with each other, the amplitude of the resulting wave becomes na and hence the intensity of laser is proportional to n2a2. So 1mW He-Ne laser is highly intense than the sun.
In an ordinary light source, the light spreads out uniformly in all directions. If you look at a 100 Watt lamp filament from a distance of 30 cm, the power entering your eye is less than 1/1000 of a watt. If you look laser beam X(caution: don’t do it at home, direct laser light can damage your eyes)X, then all the power in the laser would enter your eye. Thus, even a 1 Watt laser would appear many thousand times more intense than 100 Watt ordinary lamp.
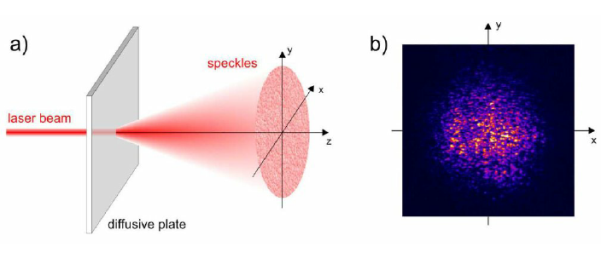
5. Laser Speckles The term speckle refers to a random granular pattern which can be observed when a highly coherent light beam is diffusely reflected at a surface with a complicated structure. This phenomenon results from the interference of different reflected portions of the incident beam with random relative optical phases.
Even minor changes of the conditions, such as of the illuminated spot or the direction of the incident laser beam, can change the detailed shape of a speckle pattern. When laser light which has been scattered off a rough surface falls on another surface, it forms an "objective speckle pattern". If a photographic plate or another 2-D optical sensor is located within the scattered light field without a lens, a speckle pattern is obtained whose characteristics depend on the geometry of the system and the wavelength of the laser.
Q9) What is coherence? A9) Definition:- A predictable correlation of the amplitude and phase at any one point with other point is called coherence.
Two waves are said to be coherent, the waves must have
In case of convectional light, the property of coherence exhibits between a source and its virtual source where as in case of laser the property coherence exists between any two of more light waves.
There are two types of coherence i) Temporal coherence ii) Spatial coherence
Temporal coherence (or longitudinal coherence):- The predictable correlation of amplitude and phase at one point on the wave train w .r. t another point on the same wave train, then the wave is said to be temporal coherence
To understand this, let us consider two points P1 and P2 on the same wave train, which is continuous as in shown in figure.
Suppose the phase and amplitude at any one point is known, then we can easily calculate the amplitude and phase for any other point on the same wave train by using the wave equation y= a sin ( Where ‘a’ is the amplitude of the wave and ‘x’ is the displacement of the wave at any instant of time‘t’.
Spatial coherence (or transverse coherence) The predictable correlation of amplitude and phase at one point on the wave train w. r .t another point on a second wave, then the waves are said to be spatial coherence (or transverse coherence)
Q10) Discuss Applications Of Lasers In various fields? A10)Applications of lasers because of unique property of laser beam such as coherence, monochromacity, directionality, and high intensity, they are widely used in various fields like 1. Communication 2. Computers 3. Chemistry 4. Photography 5. Industry 6. Medicine 7. Military 8. Scientific Research 1. Communication In case of optical communication semiconductors laser diodes are used as optical sources and its band width is (1014Hz) is very high compared to the radio and microwave communications. More channels can be sent simultaneously Signal cannot be tapped as the band width is large, more data can be sent. A laser is highly directional and less divergence, hence it has greater potential use in space crafts and submarine. It is used in optical fiber communications to send information over large distances with low loss. Laser light is used in underwater communication networks. Lasers are used in space communication, radars and satellites.
2. Computers In LAN (local area network), data can be transferred from memory storage of one computer to other computer using laser for short time. Lasers are used in CD-ROMS during recording and reading the data. Lasers are used in computer printers.
3. Chemistry Lasers are used in molecular structure identification Lasers are also used to accelerate some chemical reactions. Using lasers, new chemical compounds can be created by breaking bonds between atoms are molecules.
4. Photography Lasers can be used to get 3-D lens less photography. Lasers are also used in the construction of holograms.
5. Industry Lasers can be used to blast holes in diamonds and hard steel. Lasers are also used as a source of intense heat Carbon dioxide laser is used for cutting drilling of metals and non-metals, such as ceramics plastics glass etc. High power lasers are used to weld or melt any material. Lasers are also used to cut teeth in saws and test the quality of fabric. It is used to cut glass and quartz, used in electronic industries for trimming the components of Integrated Circuits (ICs).Lasers are used for heat treatment in the automotive industry. Laser light is used to collect the information about the prefixed prices of various products in shops and business establishments from the bar code printed on the product. Ultraviolet lasers are used in the semiconductor industries for photolithography. Photolithography is the method used for manufacturing printed circuit board (PCB) and microprocessor by using ultraviolet light. It is also used to drill aerosol nozzles and control orifices within the required precision.
6. Medicine Pulsed neodymium laser is employed in the treatment of liver cancer. Argon and carbon dioxide lasers are used in the treat men of liver and lungs. Lasers used in the treatment of Glaucoma. Lasers used in endoscopy to scan the inner parts of the stomach. Lasers used in the elimination of moles and tumors which are developing in the skin tissue and hair removal. It is also used for bloodless surgery. Lasers are used to destroy kidney stones, in cancer diagnosis and therapy also used for eye lens curvature corrections. Lasers are used to study the internal structure of microorganisms and cells. It is used to create plasma. Lasers are used to remove the caries or decayed portion of the teeth.
7. Military Lasers can be used as a war weapon. High energy lasers are used to destroy the enemy air-crofts and missiles. Lasers can be used in the detection and ranging likes RADAR. Laser range finders are used to determine the distance to an object. The ring laser gyroscope is used for sensing and measuring very small angle of rotation of the moving objects. Lasers can be used as a secretive illuminators for reconnaissance during night with high precision.
8. Scientific research Lasers are used in the field of 3D-photography Lasers used in Recording and reconstruction of hologram. Lasers are employed to create plasma. Lasers are used in Raman spectroscopy to identify the structure of the molecule and to count the number of atoms in a substance. Lasers are used in the Michelson- Morley experiment. A laser beam is used to confirm Doppler shifts in frequency for moving objects. A laser helps in studying the Brownian motion of particles. With the help of a helium-neon laser, it was proved that the velocity of light is same in all directions. Lasers are used to measure the pollutant gases and other contaminants of the atmosphere. Lasers help in determining the rate of rotation of the earth accurately. Lasers are used for detecting earthquakes and underwater nuclear blasts. A gallium arsenide diode laser can be used to setup an invisible fence to protect an area.
Q11) Write a note on the applications of an optical fibre? A11) Application of optical fibre
Q12) Write down properties of x-rays ? A12)
Q13) Write down Applications of X – Rays? A13) X-rays are types of electromagnetic radiation probably most well-known for their ability to see through a person's skin and reveal images of the bones beneath it. Advances in technology have led to more powerful and focused X-ray beams as well as ever greater applications of these light waves from imaging teeny biological cells and structural components of materials like cement to killing cancer cells. Most people are familiar with x-rays because of their use in medical imaging but there are many other applications of the radiation:
Q14) What is Compton Effect? Write result and conclusion of Compton experiment? A14) In his 1923 experiment, Compton provided the most conclusive confirmation of the particle aspect of radiation.
By scattering X-rays off free electrons, he found that the wavelength of the scattered radiation is larger than the wavelength of the incident radiation. This can be explained only by assuming that the X-ray photons behave like particles.
According to classical physics, the incident and scattered radiation should have the same wavelength. Also we know that the energy of the X-ray radiation is too high to be absorbed by a free electron therefore the incident X-ray would then provide an oscillatory electric field which sets the electron into oscillatory motion, hence making it radiate light with the same wavelength but with an intensity I that depends on the intensity of the incident radiation I0
But neither of these two predictions of classical physics is compatible with experiment.
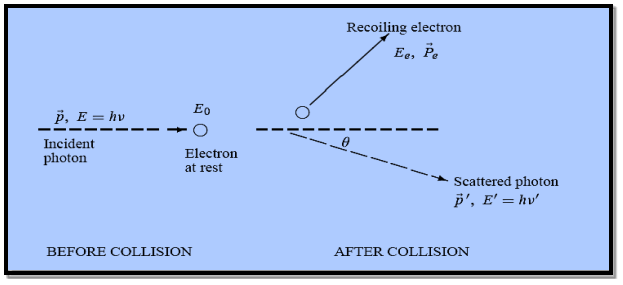
Figure: Elastic scattering of a photon from a free electron
By experiment Compton reveal that the wavelength of the scattered X-radiation increases by an amount
Compton succeeded in explaining his experimental results only after treating the incident radiation as a stream of particles—photons—colliding elastically with individual electrons.
Here we will discuss elastic scattering of a photon from a free electron as shown in figure. Consider that the incident photon, of energy E =hν and momentum p = hν /c, collides with an electron that is initially at rest. If the photon scatters with a momentum
Which leads
Energy Conservation The energies of the electron before and after the collision are given, respectively, by E0 =mec2 ………..(3)
Since the energies of the incident and scattered photons are given by E = hν and E0 = hν’, respectively, conservation of energy dictates that E + E0 = E’ + Ee ………..(4)
Which leads to
Squaring both sides of (5) and simplifying, we get
Hence wavelength shift is given by
Where λC = h/mec = 2.426 x 10-12 m is called the Compton wavelength of the electron.
This relation connects the initial and final wavelengths to the scattering angle. Compton’s experimental observation:
Q15) High energy photons are scattered from electrons initially at rest. Assume the photons are back scattered and their energies are much larger than the electron’s rest-mass energy, E = mec2. (a) Calculate the wavelength shift. (b) Show that the energy of the scattered photons is half the rest mass energy of the electron, regardless of the energy of the incident photons. (c) Calculate the electron’s recoil kinetic energy if the energy of the incident photons is 150 MeV.
A15) (a) In the case where the photons backscatter i.e. θ = π The wavelength shift becomes
(b) Since the energy of the scattered photons E’ is related to the wavelength
Where E = hc/
(c) If E = 150 MeV, the kinetic energy of the recoiling electrons can be obtained from conservation of energy Ke = E – E’
Q16) X-rays with an energy of 300 keV undergo Compton scattering with a target. If the scattered X-rays are detected at 30° relative to the incident X-rays, determine the Compton shift at this angle, the energy of the scattered X-ray, and the energy of the recoiling electron. A16) The Compton shift When it is scattered through an angle θ by an electron: λ′−λ= λe(1−cosθ) We know Compton wavelength of the electron λe= h/mec= 2.43 pm me mass of the electron = 511 keV/c2 θ = 30° Compton shift is λ′−λ= λe(1−cosθ) = 2.426 x 10-12 m (1−cos30◦.) = 0.325 pm The energy E′ of the scattered photon is E′=hc/ λ′ And λ=hc/E E=300 keV is the wavelength of the incoming photon. It follows that E′= 278 keV. By conservation of energy, the energy lost by the photon in the collision is converted into kinetic energy K of the recoiling electrons K= 22 keV
Q17) Discuss construction, working and application of molecular gas Laser?
Or
Discuss construction, working and application of CO2 Laser?
Or Discuss four level laser ?
A17) CO2 LASER In a molecular gas laser, laser action is achieved by transitions between vibrational and rotational levels of molecules. Its construction is simple and the output of this laser is continuous. In CO2 molecular gas laser, transition takes place between the vibrational states of Carbon dioxide molecules. CO2 Molecular gas laser It was the first molecular gas laser developed by Indian born American scientist Prof.C.K.N.Pillai. It is a four level laser and it operates at 10.6 μm in the far IR region. It is a very efficient laser. Energy states of CO2 molecules.
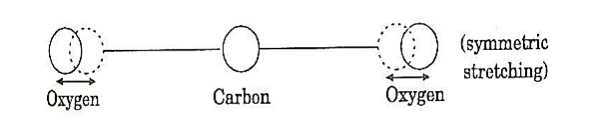
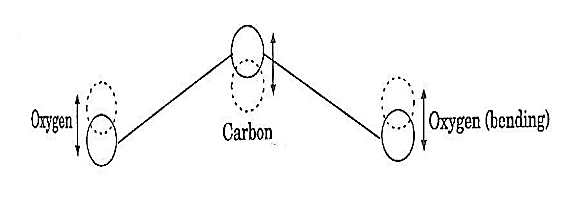
A carbon dioxide molecule has a carbon atom at the center with two oxygen atoms attached, one at both sides. Such a molecule exhibits three independent modes of vibrations. They are a) Symmetric stretching mode. b) Bending mode c) Asymmetric stretching mode. a. Symmetric stretching mode
In this mode of vibration, carbon atoms are at rest and both oxygen atoms vibrate simultaneously along the axis of the molecule departing or approaching the fixed carbon atoms.
14 Figure:
b. Bending mode:
In this mode of vibration, oxygen atoms and carbon atoms vibrate perpendicular to molecular axis.
15 Figure:
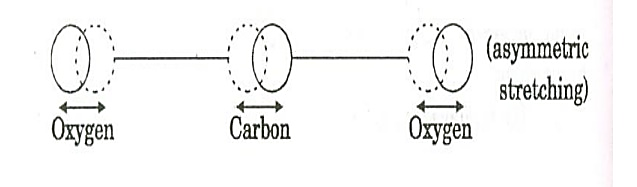
c. Asymmetric stretching mode:
16 Figure:
In this mode of vibration, oxygen atoms and carbon atoms vibrate asymmetrically, i.e., oxygen atoms move in one direction while carbon atoms in the other direction.
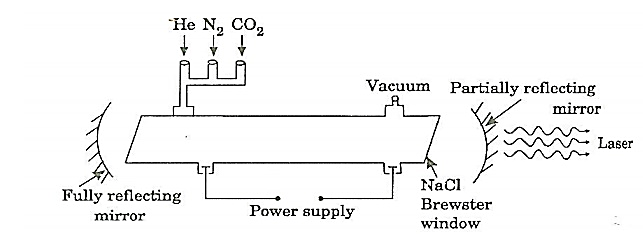
PRINCIPLE: The active medium is a gas mixture of CO2, N2 and He. The laser transition takes place between the vibrational states of CO2 molecules. CONSTRUCTION: It consists of a quartz tube 5 m long and 2.5 cm in the diameter. This discharge tube is filled with gaseous mixture of CO2 (active medium), helium and nitrogen with suitable partial pressures.
17 Figure:
The terminals of the discharge tubes are connected to a D.C power supply. The ends of the discharge tube are fitted with NaCl Brewster windows so that the laser light generated will be polarized. WORKING:
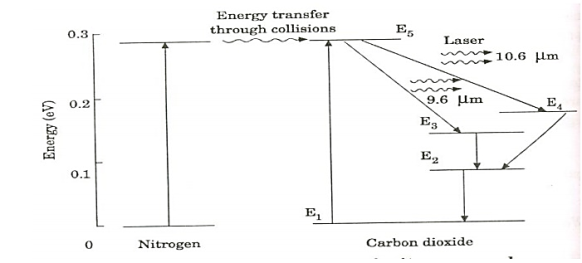
18 Figure: energy levels of nitrogen and carbon dioxide molecules When an electric discharge occurs in the gas, the electrons collide with nitrogen molecules and they are raised to excited states. This process is represented by the equation N2 + e* = N2* + e N2 = Nitrogen molecule in ground state e* = electron with kinetic energy N2* = nitrogen molecule in excited state e= same electron with lesser energy Now N2 molecules in the excited state collide with CO2 atoms in ground state and excite to higher electronic, vibrational and rotational levels. This process is represented by the equation N2* + CO2 = CO2* + N2 N2* = Nitrogen molecule in excited state. CO2 = Carbon dioxide atoms in ground state CO2* = Carbon dioxide atoms in excited state N2 = Nitrogen molecule in ground state. Since the excited level of nitrogen is very close to the E5 level of CO2 atom, population in E5 level increases. As soon as population inversion is reached, any of the spontaneously emitted photon will trigger laser action in the tube. There are two types of laser transition possible. 1. Transition E5 to E4 This will produce a laser beam of wavelength 10.6μm 2. Transition E5 to E3 This transition will produce a laser beam of wavelength 9.6μm. Normally 10.6μm transition is more intense than 9.6μm transition. The power output from this laser is 10kW. Characteristics: 1. Type: It is a molecular gas laser. 2. Active medium: A mixture of CO2 , N2 and helium or water vapour is used as active medium 3. Pumping method: Electrical discharge method is used for Pumping action 4. Optical resonator: Two concave mirrors form a resonant cavity 5. Power output: The power output from this laser is about 10kW. 6. Nature of output: The nature of output may be continuous wave or pulsed wave. 7. Wavelength of output: The wavelength of output is 0.6μm and 10.6μm.
ADVANTAGES: 1. The construction of CO2 laser is simple 2. The output of this laser is continuous. 3. It has high efficiency 4. It has very high output power. 5. The output power can be increased by extending the length of the gas tube.
DISADVANTAGES: 1. The contamination of oxygen by carbon monoxide will have some effect on laser action 2. The operating temperature plays an important role in determining the output power of laser. 3. The corrosion may occur at the reflecting plates. 4. Accidental exposure may damage our eyes, since it is invisible (infra-red region) to our eyes.
APPLICATIONS: 1. High power CO2 laser finds applications in material processing, welding, drilling, cutting soldering etc. 2. The low atmospheric attenuation (10.6μm makes CO2 laser suitable for open air communication. 3. It is used for remote sensing 4. It is used for treatment of liver and lung diseases. 5. It is mostly used in neuro surgery and general surgery. 6. It is used to perform microsurgery and bloodless operations.
Q18) Discuss X-ray notation and Auger transition ?
A18)
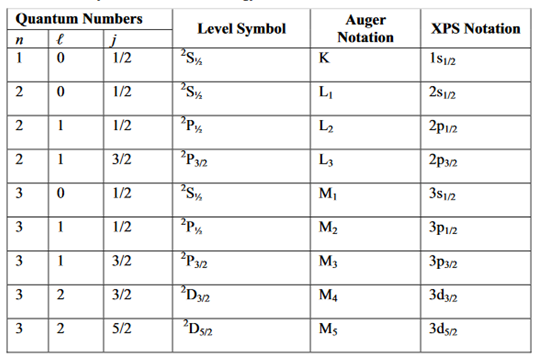
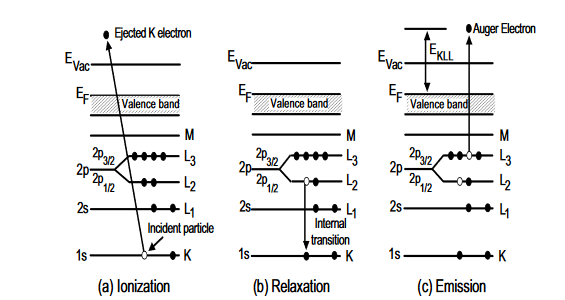
X-RAY NOTATION We now discuss the terminology used for electronic energy levels for light atoms, for which Russell-Saunders coupling (also called L-S coupling) is a valid approximation. In the general case, each level is specified by the principle quantum number (n) and a level symbol 2S+1LJ In this symbol, S is the total electronic spin angular momentum quantum number, L is the code for the total electronic orbital angular momentum quantum number, and J is the total electronic angular momentum quantum number. Because X-ray spectra are similar to one-electron alkali atom spectra, the following simplification is made to yield the XPS notation. In addition to the principal quantum number (n), the energy level can be specified with the orbital angular momentum (l) and the total angular momentum quantum number (j) of a single electron. The spin multiplicity 2S+ 1 can be ignored because it is always 2 for a one-electron (one-hole) atom since S=½. The total angular momentum of a single electron is obtained by using the Clebsch-Gordon series: j= l+s, l+s-1,………… In the above expression, l is the orbital angular momentum quantum number ands is the spin angular momentum quantum number, which is ½ for all electrons. The general form of the XPS notation is n l j. We illustrate the above discussion with a specific example involving the fine structure of the sodium D line. The excited Na atom electron configuration (1s22s22p63p) yields the 2P term because L= l =1 and S = s = ½. Using the Clebsch-Gordon series we obtain J = 1 + ½ and 1 + ½, yielding two levels (2P1/2 and 2P3/2) for the 2P term. The principal quantum number 3 is often omitted. As is often done in X-ray photoelectron spectroscopy, the above two energy levels may be written alternatively as 3p1/2 and 3p3/2. Specifying the energy levels with Auger notation involves using the letters K, L, M,... for the principal quantum number 1, 2, 3,... and a subscript that depends on the orbital quantum number (l) and the total angular momentum quantum number (j). For example, the two levels 2P1/2 and 2P3/2 —the energy levels of the excited Na atom — may be written as M2 and M3. Note that M1 is the Auger notation for the energy level of the ground state electron configuration (1s22s22p63s )of the Na atom. The level symbol for the ground state electron configuration is 2S½ corresponding to the XPS notation of 3s½.When the energy levels are very close to each other they are not usually resolvable experimentally. These unresolvable energy levels are normally designated with a comma between the subscripts (e.g., L2,3 and M4,5). We summarize the above discussion in Table 1 AUGER TRANSITIONS The Auger process for a solid is schematically illustrated in Figure 2. The KL2L3 Auger transition, illustrated in this diagram, involving ionization, relaxation, and emission, may be visualized as follows (1) A core- electron in the atom is removed by the high-energy incident Electron creating a vacancy in K shell and yielding electronically excited ion (ionization). (2) An electron from the L2 falls down almost immediately in a radiation less transition to fill the vacancy in the K shell (relaxation).
1 Table : X-ray notation of electron energy states
Figure:2
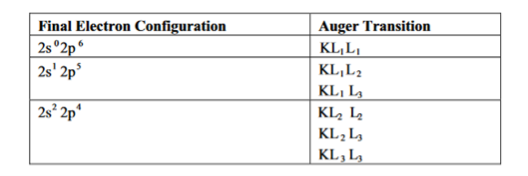
(3) Excess energy of the excited state ion is removed by the ejection of an Auger electron from the L3 level (emission). The nomenclature of the Auger transition indicates the energy levels in the order in which they are involved in the whole process. Thus, the transition described above may be designated as KL2L3. In the context of Russell-Saunders coupling, there are six KLL transitions corresponding to the three final electron configurations, as shown in Table 2
2 Table: KLL Auger transition corresponding to different final electron configuration
Although many Auger transitions are available, especially for atoms with high atomic number, most have low probabilities. Some transitions, although energetically allowed, are forbidden due to selection rules. When a valence electron is involved, the letter V is often used (e.g., KLV, KVV, and LMV). The letter C is sometimes used to denote a core level (e.g., CVV). The strongest Auger transitions are of the type ABB (e.g., KLL and LMM). Special transition of the type AAB, commonly termed Coster-Kronig transitions, are also very strong. X-ray emission is a competing process for Auger emission because the energy difference between the core and outer levels can also be released in the form of a characteristic X-ray. The sum of the Auger yield and X-ray emission yield is unity. It has been observed that the probability for X-ray emission is much lower than the Auger emission for the range of energies normally measured in AES Moreover, for elements with low atomic numbers, the cross-section for the Auger process is much higher than that for emission of X-ray photons A brief survey of the effects of interatomic Auger and Coster-Kronig transitions involving either the annihilation and or ejection of electrons associated with the ligands nearest neighbour to the hole-state atom is presented. |