undefined | unit 4 intermolecular forces and potential energy surfaces

CHEM

Unit 04Intermolecular forces and potential energy surfaces Q1) Explain Ionic interaction.A1) This is also called as the charge- charge interaction and Electrostatic interaction. It is the specific type of chemical bond formed between the metal and a non-metal. The metals that are used is Alkali metals and Alkaline earth metal of periodic table. The used non-metal are halogens. E.g. NaCl. The interaction between the different metal took place just to complete the octet and attain a stability. The term octet means that the element has an eight electron in it’s outermost shell. There is a level of covalent-bond character in each ionic bond. However the purest ionic bond never exists as because of there is a level of covalent bond character in each ionic bond. As the general rule of thumb the larger the electro-negativity differences between the metal and non-metal the more ionic the bond and therefore the less covalent the bond will be.The interactions between ions (ion - ion interactions) are the easiest to understand: like charges repel each other and opposite charges attract. These Columbic forces operate over relatively long distances in the gas phase. The force depends on the product of the charges (Z1, Z2) divided by the square of the distance of separation (d2): F = - Z1Z2/d2 Q2) Explain Induce Dipole. A2) An induced dipole moment is a temporary condition during which a neutral non-polar atom like Helium, undergoes a separation of charge due to the environment. When an instantaneous dipole atom approaches a neighboring atom, it can cause that atom to produce dipoles. The neighboring atom is then considered to have an induced dipole moment. Q3) Explain Spontaneous Dipole-Induced Interaction. A3) This is also called as the London Forces. The temporary attractive force that results when the electrons in the adjacent atoms occupy positions that make the atom form temporary dipoles. They are large networks of intermolecular forced between non-polar and non-charged molecules and atoms. The molecules that have induced dipole may also induce neighboring molecules to have dipole moment, so a large network of induced dipole interaction exists. Q4) Explain Potential Energy of Dipole Interaction.A4) Potential energy is the maximum energy that is available for an object to do work. In physics, work is a quantity that describes the energy expended as a force operates over a distance. Potential energy is positional because it depends on the forces acting on an object at its position in space. For instance, we could say that an object held above the ground has a potential energy equal to its mass x acceleration due to gravity x its height above the ground. This potential energy that an object has as a result of its position can be used to do work. For instance we could use a pulley system with a large weight held above the ground to hoist a smaller weight into the air. As we drop the large weight it converts its potential energy to kinetic energy and does work on the rope which lifts the smaller weight into the air. It is important to remember that due to the second law of thermodynamics, the amount of work done by an object can never exceed (and is often considerably less) than the objects potential energy. On a subatomic level, charged atoms have an electric potential which allows them to interact with each other. Electric potential refers to the energy held by a charged particle as a result of it's position relative to a second charged particle. Electric potential depends on charge polarity, charge strength and distance. Molecules with the same charge will repel each other as they come closer together while molecules with opposite charges will attract. For two positively charged particles interacting at a distance r, the potential energy possessed by the system can be defined using Coulomb's Law:V=kQq/r Q5) Explain the difference type of Vander Waal Interaction. A5)

(i) Ion-dipole interaction: The force that exerts between the cation or anion with presence of another polar molecule. E.g. It can be seen in HCl. The Hydrogen and Cl of same molecule are bonded with ionic bond while it is further attached to other component of same element with Vander Waal Forces.

(ii) Dipole-Dipole Interaction: This is the interaction between 2 different polar molecules. This is one of the second strongest Vander Waal Forces.

(iii) Ion-Induced Dipole Interaction: In the type of Vander Waal interaction one molecule is ionic while other one is non-polar molecule. The non-polar molecule induced by the effect of first element.

(iv) Dipole-Induced Dipole Interaction: In this type of Vander Waal interaction there are one polar and other one non-polar molecule. So the polar molecule makes the non-polar molecule to be polarized.

(v) Instantaneous Dipole-Induced Dipole Interaction: In this the both molecule are non-polar. The first molecule is become polarized instantly on the condition when the electron of a molecule revolving around the nucleus and at the instant time at which all the electron are oriented at a single place and hence that tend to result in the formation of another non-polar molecule to be polarized. This is also called as the London Forces or Dispersion Forces.

Q6) Enlist the characteristics of Vander Waal Forces.A6) The main characteristics of van der Waals forces are:

They are weaker than normal covalent and ionic bonds.

Van der Waals forces are additive and cannot be saturated.

They have no directional characteristic.

They are all short-range forces and hence only interactions between the nearest particles need to be considered (instead of all the particles). Van der Waals attraction is greater if the molecules are closer.

Vander Waals forces are independent of temperature except for dipole – dipole interactions.

Q7) Explain the crritical phenomena.A7) The essential condition for the liquefaction of the gas is described by the study of critical temperature, critical pressure and critical volume and their inter relationships.

When a gaseous system is transformed to its liquid state, there is a tremendous decrease in the volume. This decrease in volume can be effectively brought about by lowering of temperature or by increasing pressure. In both these effects the gaseous molecules come closer to each other and experience an increase in force of attraction which results in liquefaction of gases. At any constant temperature when pressure is increased volume is decreased and vice versa. Such P-V curves at constant temperature are known as isotherms.

The figure shows the continuous decrease in pressure with increase in volume for both ideal and real gases. There is a definite deviation exhibited by the real gas from ideal gas behavior at high pressure and low volumes. Critical temperature (Tc) It is defined as the characteristic temperature of a gas at which increase in pressure brings in liquefaction of gas above which no liquefaction occurs although the pressure may be increased many fold. For instance Tc of CO2 is 31.1 o C. This means that it is not possible to liquefy CO2 by applying pressure when its temperature is above 31.1 o C. Critical pressure (Pc)It is defined as the minimum pressure required to liquefy 1 mole of a gas present at its critical temperature.Critical volume (Vc) The volume occupied by 1 mole of a gas at its critical pressure and at critical temperature is the critical volume (Vc) of the gas. A gas is said to be at its critical state when its pressure, volume and temperature are Pc, Vc and Tc. Q8) Derive Vander Waal forces for one mole of gas.

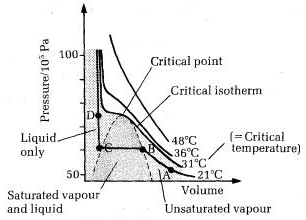
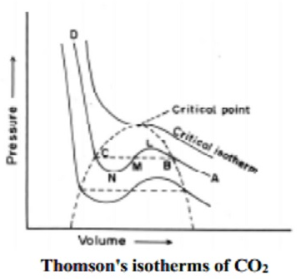
A8) For a real gas, using Vander Waals equation, the volume of a real gas is given as (Vm – b), where b is the volume occupied by per mole.

Therefore, ideal gas law when substituted with V = Vm – b is given as:

P(Vm−b)=nRT

Because of intermolecular attraction P was modified as below

(P+aV2m)(Vm−b)=RT (P+an2V2)(V−nb)=nRT

Where,

Vm: molar volume of the gas

R: universal gas constant

T: temperature

P: pressure

V: volume

Thus, Vander Waals equation can be reduced to ideal gas law as PVm = RT.

Vander Waals Equation Derivation for one mole of gas:

Following is the derivation of Vander Waals equation for one mole of gas that is composed of non-interacting point particles which satisfies ideal gas law:

p=RTVm

=RTv p

=RTVm−b C

=NaVm

(proportionality between particle surface and number density)

a′C2=a′(NA/VM)2

=a/V2m p

=RT/(Vm−b)−(a/V2m)

⇒(p+aV2m)(Vm−b)

=RT (p+n2a/V2)(V−nb)

=nRT (substituting nVm = V)

Van der Waals equation applied to compressible fluids:

Compressible fluids like polymers have varying specific volume which can be written as follows:

(p+A)(V−B)=CT

Where,

p- pressure

V- specific volume

T- temperature

Q9) Explain Entropy.A9) Entropy is used to describe the behavior of a system in terms of thermodynamic properties such as temperature, pressure, entropy, and heat capacity. This thermodynamic description took into consideration the state of equilibrium of the systems.Meanwhile, the statistical definition which was developed at a later stage focused on the thermodynamic properties which were defined in terms of the statistics of the molecular motions of a system. Entropy is a measure of the molecular disorder. Q10) Derive Gibbs’ Free energy.

A10) Gibbs free energy of the system is the difference of enthalpy of the system with the product of temperature times the entropy of the system.

G=H-TS

Gibbs free energy of the system is defined in term of the thermodynamics which are state in function. Any change in the Gibbs Free Energy System is directly proportional to the difference of change in the enthalpy of the system with the products of temperature times the entropy of the system.

G= H- (TS)

While at constant temperature this reaction transform into:

G= H-T S

The Nernst Equation is derived from the Gibbs free energy under standard conditions.

E*=E*reduction-E*oxidation ………..(i)

G=-nFE ………..(ii)

Where,

n=no. of transferred electrons in the reaction

F= Faraday constant

E=Potential Difference.

While when we see in the standard condition then, equation (ii) becomes

G*=-nFE* ………….(iii)

Hence,

Reaction is Spontaneous when E* is positive while non- spontaneous in vice-versa.

G= G*+RT lnQ ………….(iv)

Now, Substituting G=−nFE and G*=−nFE* into Equation 4, we have:

−nFE=−nFEo+RTlnQ …………….(v)

On Dividing both sides of the Equation above by −nF,

E=E*−RTnFlnQ(6) ……….(vi)

Equation (vi) in the form of log10:

E=E*−2.303RT/nF log10Q …….(vii)

At standard temperature T = 298 K, the 2.303RT/F term equals 0.0592 V and Equation

(vii) can be rewritten:

E=E*−0.0592V/n log10Q ……..(viii)

The equation (viii) clearly indicates that electric potential of cell depends on reaction quotient of reaction. The product formation leads to the increase in the concentration of the products. This tends to decrease the the potential of the cell until it reaches at the stage of equilibrium where, G=0 and G=-nFE Q=K so E=0

Then on substituting the these values to Nernst Equation we get,

0=E*-RT/nF In K …….(ix)

At room temperature it becomes;

0=E*-0.0592V/n Log10K

LogK=nE*/0.0592V

The above equation clearly indicates the equilibrium constant K is proportional to the standard potential.

Sign Up