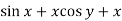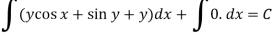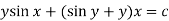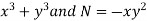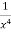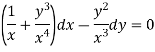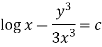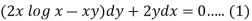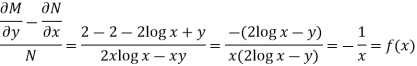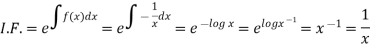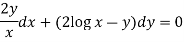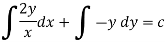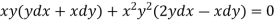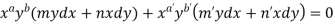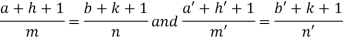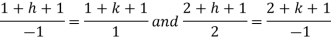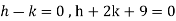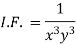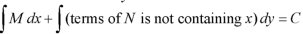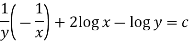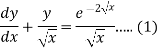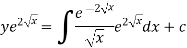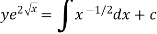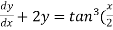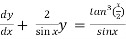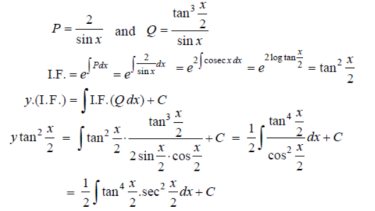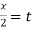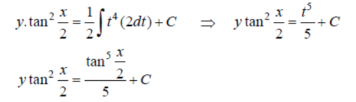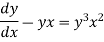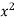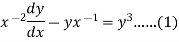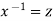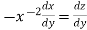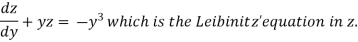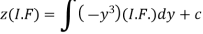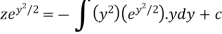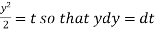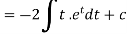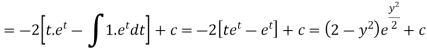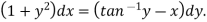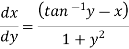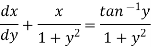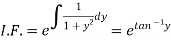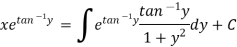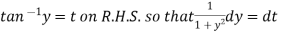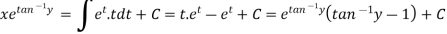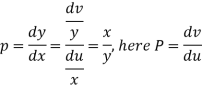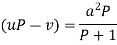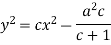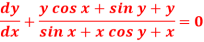
S1) We can write the equation as below-

Here M = and N =

So that-

The equation is exact and its solution will be-

Or

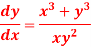
S2)

We can write the given equation as-

Here,

M =

Multiply equation (1) by we get-

This is an exact differential equation-

S3)

Here given,

M = 2y and N = 2x log x - xy

Then-

Here,

Then,

Now multiplying equation (1) by 1/x, we get-

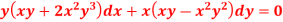
S4)

We can write the equation as below-

Now comparing with-

We get-

a = b = 1, m = n = 1, a’ = b’ = 2, m’ = 2, n’ = -1

I.F. =

Where-

On solving we get-

h = k = -3

Multiply the equation by , we get-

It is an exact equation.

So that the solution is-

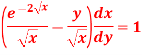
S5) We can write the given equation as-

So that-

I.F. =

The solution of equation (1) will be-

Or

Or

Or

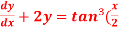S6)  here we have,

sin x )

which is the linear form,

Now,

             Put tan   so that  sec² dx =  dt, we get

 Which is the required solution.

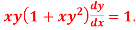
S7)

We can write the equation as-

On dividing by , we get-

Put so that

Equation (1) becomes,

Here,

Therefore the solution is-

Or

Now put

Integrate by parts-

Or
 

S8) here given-

We can re-write this as-

Which is a linear differential equation-

The solution will be-

Put

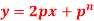
S9)

Here we have-

Now differentiate it with respect to x, we get-

Or

This is the Leibnitz’s linear equation in x and p, here

Then the solution of (2) is-

Or

Or

Put this value of x in (1), we get

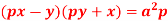
S10)

Put

So that-

Then the given equation becomes-

Or

Or

Which is the Clairaut’s form.

Its solution is-

i.e.