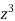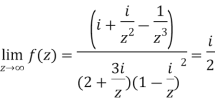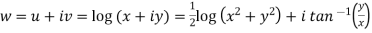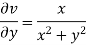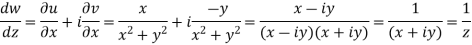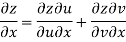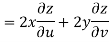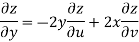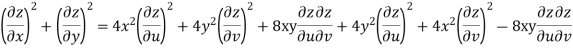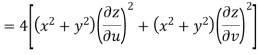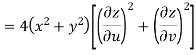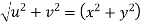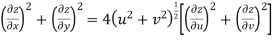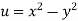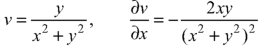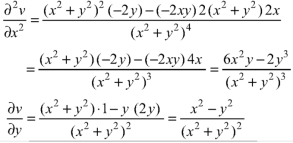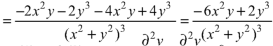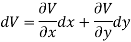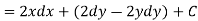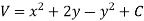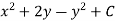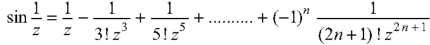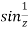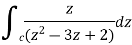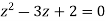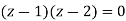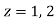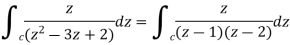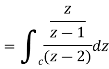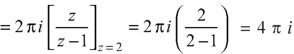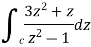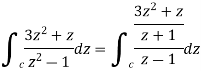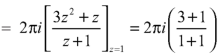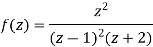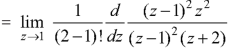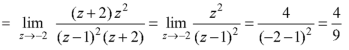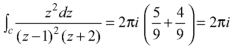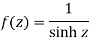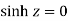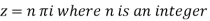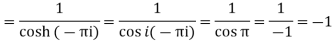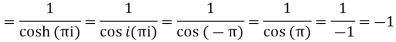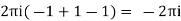S1) Here we have-
Divide numerator and denominator by
|
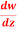 . Also determine where w is non-analytic.
. Also determine where w is non-analytic.S2) Here we have Therefore-
Again-
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0). So that w is analytic everywhere but not at z = 0
|
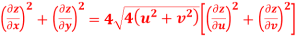
S3) Given that
Since
V=2xy
Now
But
Hence |
 and
and 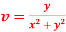 are harmonic functions of (x, y).
are harmonic functions of (x, y).S4) We have Now
Here it satisfies Laplace equation so that u (x, y) is harmonic. Now-
On adding the above results- We get-
So that v(x, y) is also a harmonic function. |
S5) We have, U(x, y) = 2x (1 – y) Let V is the harmonic conjugate of U. So that by total differentiation,
Hence the harmonic conjugate of U is |
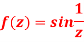
S6) As we know that-
So that there is a number of singularity.
(1/z = ∞ at z = 0) |
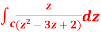 by using Cauchy’s integral formula.Here c is the circle |z - 2| = 1/2
by using Cauchy’s integral formula.Here c is the circle |z - 2| = 1/2S7) it is given that-
Find its poles by equating denominator equals to zero.
There is one pole inside the circle, z = 2, So that-
Now by using Cauchy’s integral formula, we get-
|
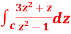 if c is circle |z - 1| = 1.
if c is circle |z - 1| = 1.S8) Here we have-
Find its poles by equating denominator equals to zero.
The given circle encloses a simple pole at z = 1. So that-
|
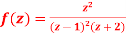 and hence evaluate-
and hence evaluate-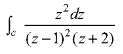 Where c: |z| = 3.
Where c: |z| = 3.S9)
The poles of the function are-
The pole at z = 1 is of second order and the pole at z = -2 is simple- Residue of f(z) (at z = 1)
Residue of f(z) ( at z = -2)
|
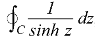 Where C is the circle |z| = 4.
Where C is the circle |z| = 4.S10) Here we have,
Poles are given by-
Out of these, the poles z = -πi , 0 and πi lie inside the circle |z| = 4. The given function 1/sinh z is of the form Its poles at z = a is Residue (at z = -πi)
Residue (at z = 0)
Residue (at z = πi)
Hence the required integral is = |