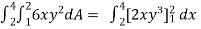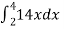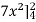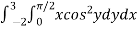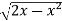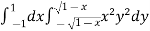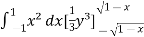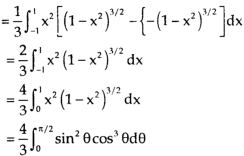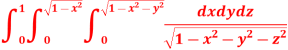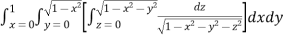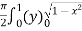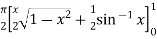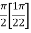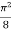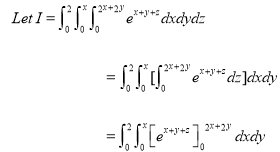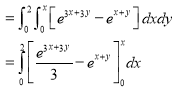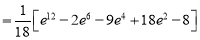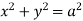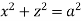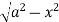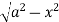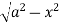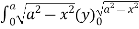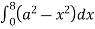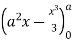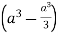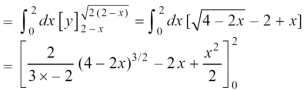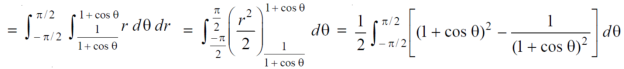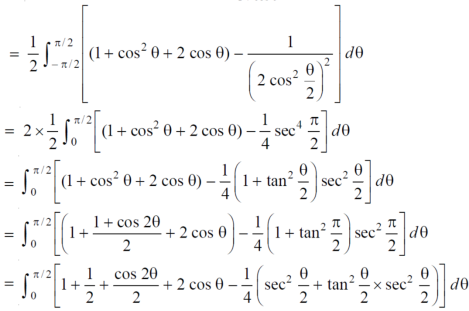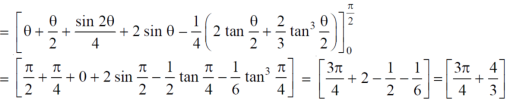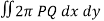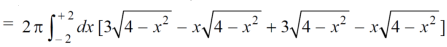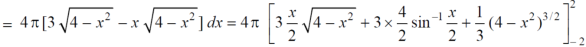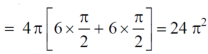, where dA is the small area in xy-plane.
S1) Let , I = = = = = 84 sq. unit. Which is the required area. |
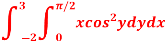
S2) Let, I = On solving the integral, we get
|
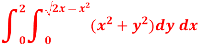
S3) Here limits of y, y = y² = 2x - x² x² + y² = 2x x² + y² - 2x = 0 ………………(1)
Eq. (1) represent a circle whose radius is 1 and centre is ( 1, 0) Lower limit of y is zero. Region of integration in upper half circle, First we will covert into polar coordinates, By putting x by r cos θ and y by r sinθ , dy dx by r drdθ,
limits of r are 0 to 2 cosθ and limits of θ are from 0 to π / 2.
|
S4) Let the integral, I = =
Put x = sinθ
= π / 24 ans. |
Q5) Evaluate
S5) Let I = = (Assuming m = = = = = = = = I = |
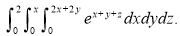
S6)
|
,
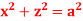
S7) For given cylinders,
Z varies from Z=- Y varies from y= - x varies from x= -a to x = a By symmetry, Required volume= 8 (volume in the first octant) =8 =8 = 8 =8 =8 =8 Volume = 16 |
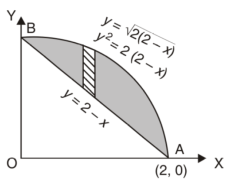
S8) Let, y = 2 – x ………………..(1) and y² = 2 (2 – x) ………………..(2) on solving eq. (1) and (2) we get the intersection points (2,0) and (0,2) , we know that, Area =
Here we will find the area as below, Area =
Which gives, = ( - 4 + 4 /2 ) + 8 / 3 = 2 / 3. |
S9) Let, r = 1 + cosθ ……………………..(1) r(1 + cosθ) = 1……………………..(2) solving these equestions , we get (1 + cosθ )(1 + cosθ ) = 1 (1 + cos θ) ² = 1 1 + cos θ = 1 cosθ = 0 θ = ±π / 2 so that, limits of r are, 1 + cosθ and 1 / 1 + cosθ The area can be founded as below,
|
S10) We know that, Volume = Here , PQ = 3 – x, =
The volume is 24π². |
