Unit III | unit 3 fluids

BME

Unit III

Fluids

Question Bank

QUESTION 1) Explain difference between Viscosity and Density?

Answer 1)

There is no direct relation between viscosity and density. However, both Viscosity and density are affected by temperature. Which implies, for any given fluid, when the temperature is raised, the particle in it start to move apart, bringing down fluid density thereby the value of viscosity also falls down or fluid becomes less viscous.

In general, for any fluids, when the temperature is increased, its density decreases, thus the fluid becomes less viscous.

Kinematic Viscosity

In fluids, Kinematic viscosity is the ratio of dynamic viscosity to density. Mathematically given by-

ν=η / ρ

Where,

ν is the Kinematic viscosity.
η is the dynamic viscosity / Absolute viscosity.
ρ is the density.

Refer to the table given below for definition, units, and symbol for the above parameter.

	Definition	SI unit	Symbol
Kinematic Viscosity	The ratio of dynamic viscosity to density	m2/s	ν
Dynamic viscosity	The measure of internal resistance against the flow	Ns/m2	η
Density	The ratio of mass per volume	Kg/m3	ρ

Viscosity and Density of Water

The table given below gives the values of Viscosity and Density of water at 100C and 200C.

Temperature	100C	200C
Viscosity (mPa.s)	1.308	1.002
Density (g/m3)	0.99975	0.99804

Viscosity and Density of Air

The table given below gives the values of Kinematic Viscosity and Density of air at -100C, -150C and -200C.

Temperature 0C	Density (Kg/m3)	Kinematic viscosity(m2/s)
-20	1.3958	1.1622×10-5
-15	1.3687	1.2039×10-5
-10	1.3426	1.2462×10-5

Question 2) A fluid moves through a tube of 15 m/s, the tube has a transverse area of 0.4 m2. If the density of the fluid is ρ = 1.5 grams/m3, what is the amount of mass flowing through the tube?

Answer 2)
To calculate the total mass of fluid flowing through the tube, we use

Mass flow rate=ρ.A.V

Substituting the values in the above equation, we get

Mass flow rate=1.5×15×0.4=9g/s

Question 3) Explain the Coefficient of Viscosity Formula

Answer 3) the force of friction between two layers of fluid having the area in square centimetre and separated by distance will have a velocity is given by:

FμAdV/dx

f=ηAdV/dx

Here,

η is coefficient of viscosity

DV/dx is velocity gradient

If dx is 1cm, A is 1cm2 and dv is 1cm/s

Then, f=η

The coefficient of viscosity is defined as the force of friction that is required to maintain a difference of velocity of 1cm/s between parallel layers of fluid. The unit is usually expressed in poise or centipoise. As we all know that viscosity is nothing but the measure of a substance’s resistance to the motion under an applied force The resulting unit is measured in centipoise which is the equivalent of 1 mPa (MilliPascal second)

The major industries where Viscosity measurements are used are in the food industry to improve the overall cost-effectiveness and maximizing production efficiency. Besides, the food industry Viscosity is also primarily used in other industries such as Adhesives, Petroleum, Concrete, and Cosmetics industry.

Question 4) Calculate the pressure in the hose whose absolute pressure is 1.01 x 105 N.m-2 if the speed of the water in hose increases from 1.96 m.s-1 to 25.5 m.s-1. Assume that the flow is frictionless and density 103 kg.m-3

Answer 4): Given,

Pressure at point 2, p2 = 1.01 × 105 N.m-2

Density of the fluid, ρ = 103 kg.m-3

Velocity of the fluid at point 1, v1 = 1.96 m.s-1

Velocity of the fluid at point 2, v2 = 25.5 m.s-1

From Bernoulli’s principle for p1,

p1=p21/2 ρv22 −1/ 2ρv21=p2+1/2ρ(v22−v21)

Substituting the values in above equation, we get

p1= (1.01×105) + 1/2(103)[(25.5)2−(1.96)2]

p1 = 4.24 × 105 N.m-2

QUESTION 5) Water is flowing through a pipe of 5 cm diameter under a pressure of 29.43 N/cm2 (gauge) and with mean velocity of 2.0 m/s. Find the total head or total energy per unit weight of the water at cross -section, which is 5 cm above the datum line.

Answer 5)

Diameter of the pipe = 5 cm = 0.5 m.

Pressure = 29.43 N/cm2 = 29.23 N/m2

Velocity v = 2.0 m/s.

Datum head z = 5 m

Total head = Pressure head + Velocity head + Datum head

Pressure head = (p/?g) 4 / (2X9=(.81)) 29=30.m43X10

Kinetic head = (v2/ 2g) = (2X2/(2X9.81)) = 0.204 m

Total head 2

= (p/+ (v(?g))/2g)+z

= 30 + 0.204 + 5 = 35.204m

Question 6) Explain limitations of Bernoulli equation

Answer 6) Limitations of the Applications of Bernoulli’s Equation

One of the restrictions is that some amount of energy will be lost due to internal friction during fluid flow. This is because fluid has separate layers and each layer of fluid will flow with different velocities. Thus, each layer will exert some amount of frictional force on the other layer thereby losing energy in the process.

The proper term for this property of the fluid is viscosity. Now, what happens to the kinetic energy lost in the process? The kinetic energy of the fluid lost in the process will change into heat energy. Therefore, we can easily conclude that Bernoulli’s principle is applicable to non-viscous fluids (fluids with no viscosity).

Another major limitation of this principle is the requirement of the incompressible fluid. Thus, the equation does not consider the elastic energy of the fluid. However, elastic energy plays a very important role in various applications. It also helps us to understand the concepts related to low viscosity incompressible fluids.

Furthermore, Bernoulli’s principle is not possible in turbulent flows. This is because the pressure and velocity are constantly fluctuating in case of turbulent flow.

Question 7) What will happen to Bernoulli’s equation if a fluid is at rest or the velocity is zero?

Answer 7) when the velocity is zero, the equation will become

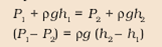
This equation is the same as the equation of pressure with depth, that is,

P2 − P1 = ρgh.

Question 8) Explain difference between pump and motor?

Answer 8)

Differences	Pump	Motor
Definition	The pump can be defined as it is a mechanical device used to convert torque from mechanical hydraulic. It simply makes possible of fluids movement from one location to another with the help of pressure or suction	Electric motors are electromechanical devices mainly used for changing energy from electrical to mechanical.
Operation	A pump is used to move fluids by using forces like air. Air moves forward from the way because the moving element starts to move. Generally, these are activated with electric motors that drive a compressor. Thus, a partial vacuum can be created because of the water movement, later it is filled with additional air.	The electric motor works on the principle of Faraday’s law of electromagnetic induction, and this law is one of the main electromagnetism laws.
Function	Pumps use different energy sources for rotating its compressor & exclusive of a driving force of the air. These use the shaft’s rotary movement which performs like the input energy for generating pressure.	Electric motor interacts with the motor’s magnetic field & winding current is used to produce power in order to generate energy from mechanical to electrical.
Types	Generally, pumps are categorized into two type’s namely positive displacement as well as centrifugal. Pumps are further classified based on the displacement method into gravity, impulse, velocity, valveless, & steam pumps.	Electrical motors are generally categorized into AC type and DC type. Where, AC type motors are classified into synchronous motors & asynchronous motors, and DC type motors are classified into brushed motors & brushless motors.
Applications	The applications of pumps mainly involve in both commercials as well as industrial like water treatment plants, paper mills, car washes, etc. The pumps like centrifugal are employed for industrial & energy applications for different functions.	The applications of electrical motors mainly include in fans, conveyor systems, compressors, dishwashers, electric vehicles, robotics, lifts, hoists, vacuum cleaners, lathes, shearing machines, grinders, and more.

Question 9) Explain the Difference between Impulse and Reaction turbine?

Answer 9)

SL NO	IMPULSE TURBINE	REACTION TURBINE
1	All hydraulic energy is converted into kinetic energy by a nozzle.	Only some amount of the available energy is converted into kinetic energy.
2	It requires very little maintenance.	Here it’s required more maintenance.
3	The degree of reaction is zero.	The degree of reaction is between ‘0’ & ‘1’
4	It needs a low discharge of water.	It needs medium and high discharge of water.
5	Water flow is a tangential direction to the turbine wheel.	Water flow is a radial and axial direction to the turbine wheel.
6	Here is having more hydraulic efficiency.	It’s having relatively less efficiency.
7	Impulse turbine operates at high water heads.	It operates at medium and low heads.
8.	An example of an impulse turbine is the Pelton wheel.	An example of a reaction turbine is Francis, Kaplan turbine.
9	Flow regulation is done by means of a needle valve fitted into the nozzle.	Flow regulation is carried out by means of guide vane assembly.
10	The turbine is always installed above the tailrace and there is no draft tube used.	In the reaction turbine, the turbine is generally connected to the tailrace through a draft tube which is gradually expanding passage.
11	The turbine doesn’t run full and air has free access to the bucket.	Water completely fills at the passage between the blades and while flowing between the inlet and outlet sections does work on the blades.
12	Water is admitted only in the forms of jets. There may be one or more jets striking an equal number of buckets simultaneously.	Water is admitted over the entire circumference of the runner.

Question 10) Explain the Difference between Centrifugal pump and reciprocating pump:

Answer 10)

Sl.No	Parameter	Centrifugal Pump	Reciprocating Pump
1.	Construction	This is simple in construction.	This is complicated in construction.
2.	Head or Pressure application	This work low or medium pressure head.	But Reciprocating pump work at the High-pressure head.
3.	Discharge	Centrifugal pump, Discharge is High.	But Here, Discharge is low.
4.	Requires relief valve	In the Centrifugal pump, there is not required relief valve.	But here, it requires a relief valve.
5.	Smooth or Pulsating flow	This is having a smooth flow.	Here, This is having a pulsating flow.
6.	Delivery	Variable	Constant delivery.

7.	Self-priming	There is no any self-priming.	Here, There is self-priming
8.	Space considerations	It requires less space whereas,	The reciprocating pump requires more space.
9.	Cost	The initial cost is low.	The initial cost is higher.
10.	Power consumptions	Here, Power consumption is high.	But in the centrifugal pump, the power consumption is low.
11.	Maintenance	It requires lower maintenance.	It requires higher maintenance.
12.	Air vessel	Not required	Air vessel required in the reciprocating pump.
13.	Fluid handling	Suitable for a wide range including clean, clear, abrasive fluids, dirty water, and oil.	Suitable for clean, clear and non-abrasive fluids.

Sign Up