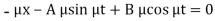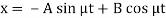Module–1

Ordinary Differential Equations-1

Question Bank

Question-1: Find the particular solution of the differential equation 5, given the boundary condition y = 1 , when x = 2.

Solution: rearrange the diff. Equation,

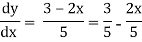
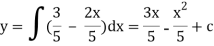
Which is the general solution.

Put the boundary conditions to find c,

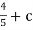-   , which gives, c = 1

   Hence the particular solution is,

                                     y = 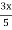- 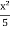+ 1.

(2) The solution of equation of the form  ,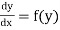

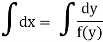
Question-2: Find the general solution of   = 3 + 2y

Solution:      here,   = 3 + 2y gives,

,

Integrating both sides,

,

By substitution,  u = (3 +2y),

                                             X =  In(3 + 2y) + c.

Question-3: Determine the particular solution of  (y² - 1)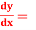3y  given that y =1  when  x = 2.

Solution:  It gives,

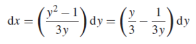
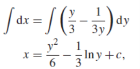
When putting the values, y =1 , x = 2 ,

The particular solution will be,

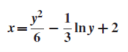
(3) The solution of equation of the form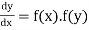 

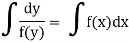
Question-4: Solve the equation 4xy = y² - 1

Solution:  on separating variables, we get

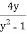                                               () dy  = dx

=  

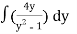   Using substitution, u = y² - 1

                                               2In(y² - 1) = In x + c.

Question-5: Solve-

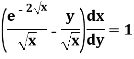
Sol. We can write the given equation as-

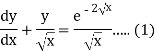
So that-

I.F. =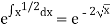

The solution of equation (1) will be-

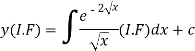
Or

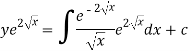
Or

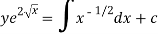
Or

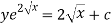
Question-6: Solve-

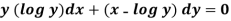
Sol.

We can write the equation as-

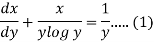
We see that it is a Leibnitz’s equation in x-

So that-

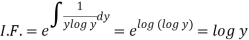
Therefore, the solution of equation (1) will be-

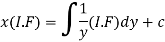
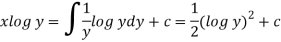
Or

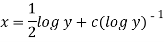
Question-7: Solve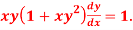

Sol.

We can write the equation as-

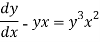
On dividing by 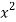, we get-

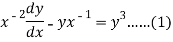
Put so that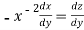

Equation (1) becomes,

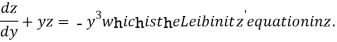
Here,

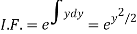
Therefore, the solution is-

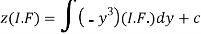
Or

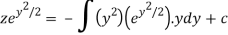
Now put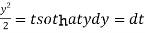

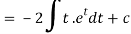
Integrate by parts-

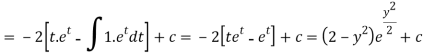
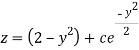
Or
 

Question-8: Solve-

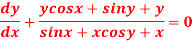
Sol. We can write the equation as below-

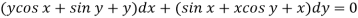
Here M = 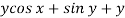and N =

So that-

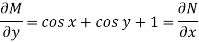
The equation is exact and its solution will be-

Or

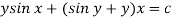
Question-9: Determine whether the differential function ydx –xdy = 0 is exact or not.

Solution.  Here the equation is the form of  M(x , y)dx + N(x , y)dy = 0

But, we will check for exactness,

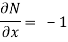
These are not equal results, so we can say that the given diff. Eq. Is not exact.

Question-10: Solve:

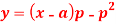
Sol.

We have-

Now differentiate (1) with respect to ‘x’, we get-

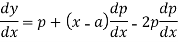
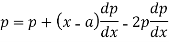
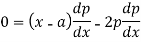
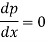
On integrating, we get p = c

Putting these values in equation (1)-

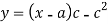
Question-11: Solve-

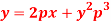
Sol.

On solving for x, we get-

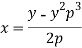
On differentiating with respect to y,

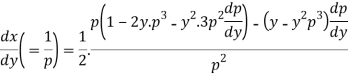
Or

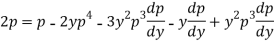
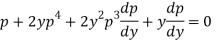
Or

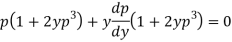
Or

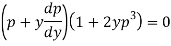
Which gives-

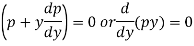
Integrating py = c

Thus, eliminate from the given equation and (1), we get-

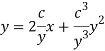
Which is the required solution.

Question-12: Solve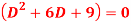

Sol.

Its auxiliary equation is-

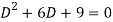
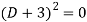
Where-

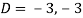
Therefore, the complete solution is-

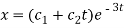
Question-13: Find the P.I. Of (D + 2)

Sol.

P.I. =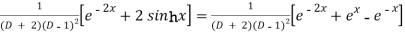

Now we will evaluate each term separately-

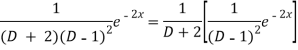
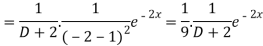
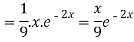
And

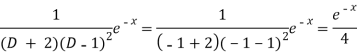
Therefore-

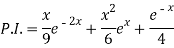
Question-14: Find the P.I. Of (D + 1) (D + D’ – 1)z = sin (x + 2y)

Sol.

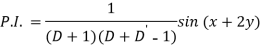
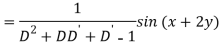
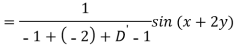
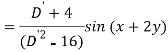
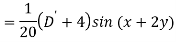
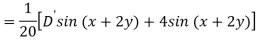
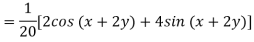
Question-15: Find P.I. Of

Sol. P.I =

Replace D by D+1

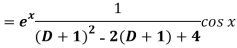
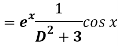
Put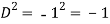

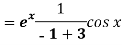
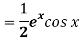
Question-16: Solve-

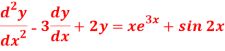
Sol.

The given equation can be written as-

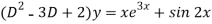
Its auxiliary equation is-

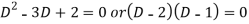
We get-

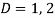
So that the C.F. Will be-

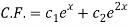
Now we will find P.I.-

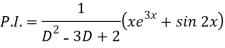
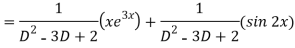
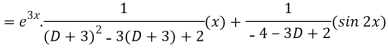
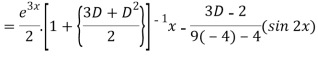
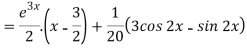
Therefore, the complete solution is-

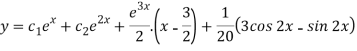
Question-17: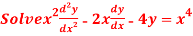

Ans. Putting,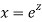

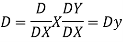
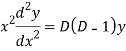
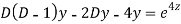
AE is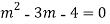

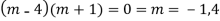
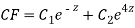
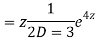
CS = CF + PI

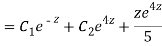
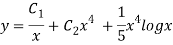
Question-18: Solve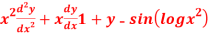 

Ans. Let,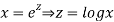

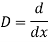
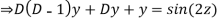
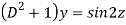
AE is

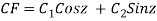
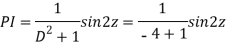
y= CF + PI

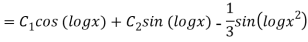
Question-19: Solve-

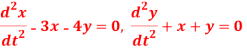
Sol.

Here we

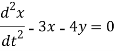
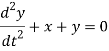
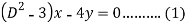
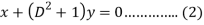
Operate equation (2) by 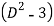, we get-

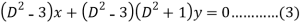
Subtract (3) from (1)-

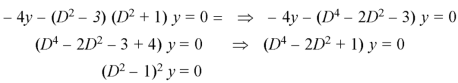
A.E-

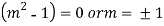
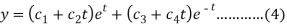
From equation (2), we get-

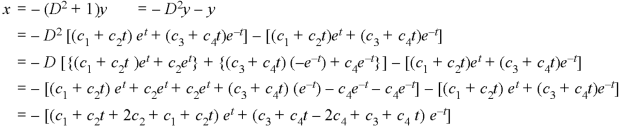
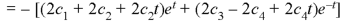
These are the required solutions.

Question-20: The equations of motions of an object are given by-

Find the path of the object.

Sol.

Put d/dt = D, then the equations become-

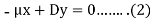
On multiplying (1) by 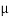and (2) by D, we get-

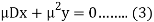
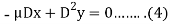
Add (3) and (4), we get-

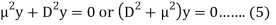
Now we need to solve (5) to get the value of y-

A.E.-

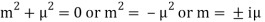
So that-

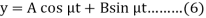
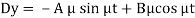
Now, on putting the value of Dy in (2), we get-