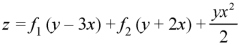Question Bank

Module–3

Partial differential equations

Question-1: Form a partial differential equation from-

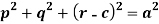
Sol.

Here we have-

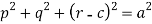
It contains two arbitrary constants a and c

Differentiate the equation with respect to p, we get-

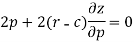
Or

Now differentiate the equation with respect to q, we get-

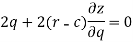
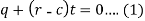
Now eliminate ‘c’,

We get

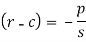
Now put z-c in (1), we get-

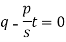
Or

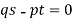
Question-2: Solve-

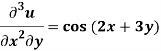
Sol.

Here we have-

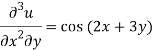
Integrate w.r.t. x, we get-

Integrate w.r.t. x, we get-

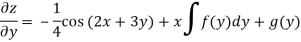
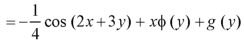
Integrate w.r.t. y, we get-

Question-3: Solve the differential equation-

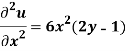
Given the boundary condition that-

At x = 0,

Sol.

Here we have-

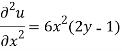
On integrating partially with respect to x, we get-

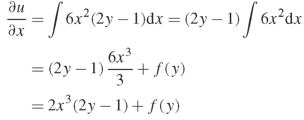
Here f(y) is an arbitrary constant.

Now form the boundary condition-

When x = 0,

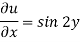
Hence-

On integrating partially w.r.t.x, we get-

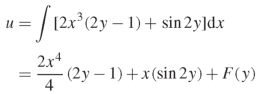
Question-4: Solve the differential equation-

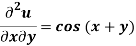
Given that 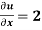when y = 0, and u = 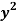when x = 0.

Sol.

We have-

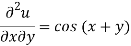
Integrating partially w.r.t. y, we get-

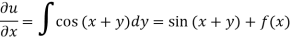
Now from the boundary conditions,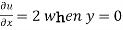

Then-

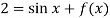
From which,

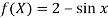
It means,

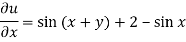
On integrating partially w.r.t. x givens-

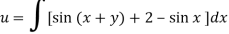
From the boundary conditions, u = 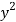when x = 0

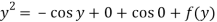
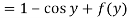
From which-

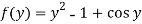
Therefore the solution of the given equation is-

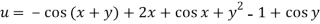
Question-5: Find the general solution of-

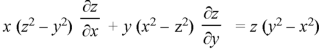
Sol. The auxiliary simultaneous equations are-

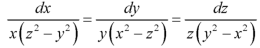……….. (1)

Using multipliers x, y, z we get-

Each term of (1) is equals to-

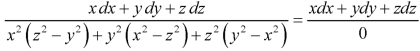
Xdx + ydy + zdz=0

On integrating-

………… (2)

Again equation (1) can be written as-

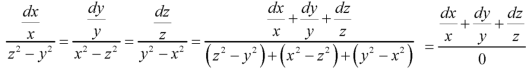
Or

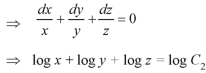
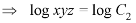
………….. (3)

From (2) and (3), the general solution is-

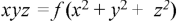
Question-6: Solve-

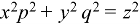
Sol.

This equation can be transformed as-

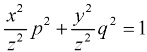
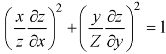
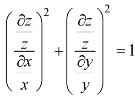………. (1)

Let

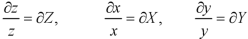
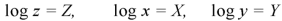
Equation (1) can be written as-

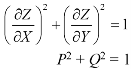………… (2)

Let the required solution be-

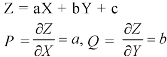
From (2) we have-

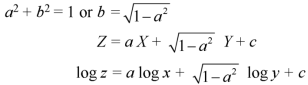
Question-7: Solve-

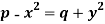
Sol.

Let-

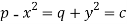
That means-

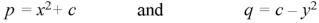
Put these values of p and q in

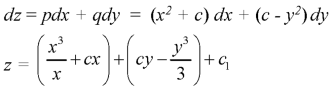
Question-9; Solve-

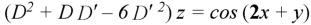
Sol.

Here we have-

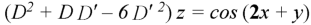
Auxiliary equation will be-

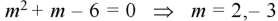
C.F.-

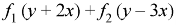
P.I.-

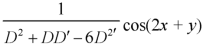
Here

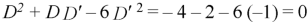
This is the case of failure.

Now-

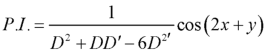
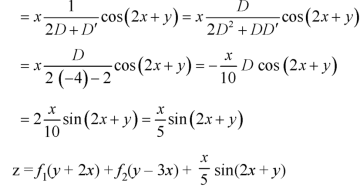
Question-10: Solve-

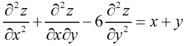
Sol.

This equation can be written as-

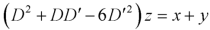
Writing D = m and D’ = 1, then the auxiliary equation will be-

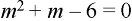
m = -3, 2

C.F.-

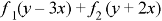
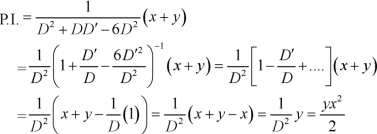
Hence the complete solution is-