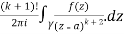Question Bank

Module–4

Functions of complex variable

Question-1: Find-

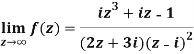
Sol. Here we have-

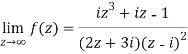
Divide numerator and denominator by 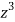, we get-

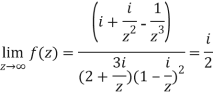
Question-2: If w = log z, then find 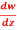. Also determine where w is non-analytic.

Sol. Here we have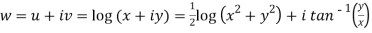

Therefore-

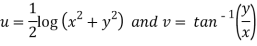
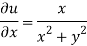
And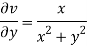
 

Again-

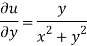
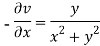
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).

So that w is analytic everywhere but not at z = 0

Question-3: Prove that the function 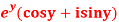is an analytical function.

Sol. Let 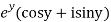=u+iv

Let 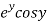=u and =v

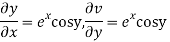
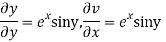
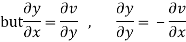
Hence C-R-Equation satisfied.

Question-4: Prove that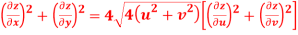

Sol. Given that

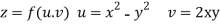
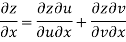
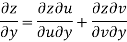
Since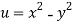      

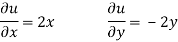
V=2xy

Now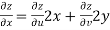

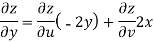
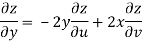
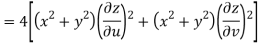
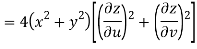
But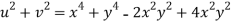                                      

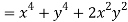
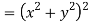
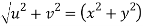
Hence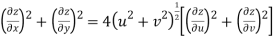 

Question-5: Check whether the function w = sin z is analytic or not.

Sol. Here-

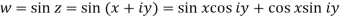
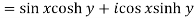
Now-

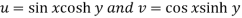
And

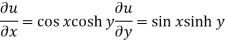
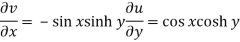
Here we see that C-R conditions are satisfied and partial derivatives are continuous.

Question-6: Evaluate along the path y = x.

Sol.

Along the line y = x,

Dy = dx that dz = dx + idy

Dz = dx + i dx = (1 + i) dx

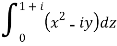
On putting y = x and dz = (1 + i)dx

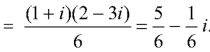
Question-7:Evaluate 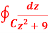where C is |z + 3i| = 2

Sol.

Here we have-

Hence the poles of f(z),

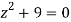
Note- put determine equal to zero to find the poles.

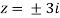
Here pole z = -3i lies in the given circle C.

So that-

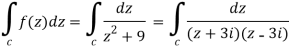
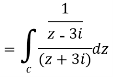
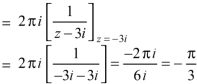
Question-8: Solve the following by cauchy’s integral method:

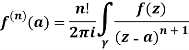
Solution:

Given,

                  =

          =

            =

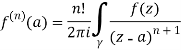
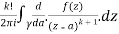
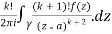
Question-9: Evaluate the integral given below by using Cauchy’s integral formula-

Sol. Here we have-

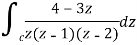
Find its poles by equating denominator equals to zero.

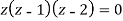
We get-

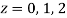
There are two poles in the circle-

Z = 0 and z = 1

So that-

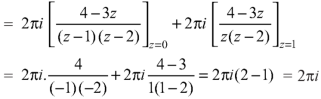
Question-10: Find the singularity of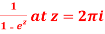

Sol.

Here we have-

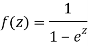
We find the poles by putting the denominator equals to zero.

That means-

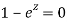
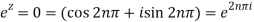
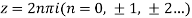
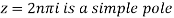
Question-11: Find the poles of the following functions and residue at each pole:

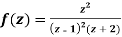and hence evaluate-

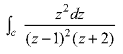where c: |z| = 3.

Sol.

The poles of the function are-

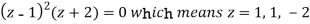
The pole at z = 1 is of second order and the pole at z = -2 is simple-

Residue of f(z) (at z = 1)

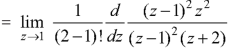
Residue of f(z) ( at z = -2)

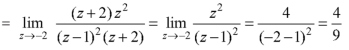
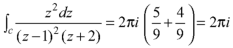
Question-12: Evaluate-

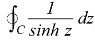
Where C is the circle |z| = 4.

Sol.

Here we have,

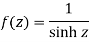
Poles are given by-

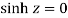
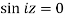
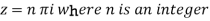
Out of these, the poles z = -πi , 0 and πi lie inside the circle |z| = 4.

The given function 1/sinh z is of the form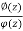

Its poles at z = a is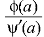

Residue (at z = -πi)

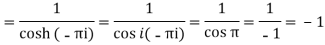
Residue (at z = 0)

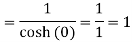
Residue (at z = πi)

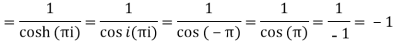
Hence the required integral is =

Question-13: Evaluate  where c;|z|=4

Sol.

Here f(z)=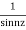

Poles are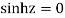

                 Sin iz=0

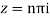
Poles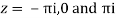

Lie inside the circle |z|=4

The given function 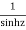is of the form

Its pole at z=a is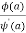

Residue (at

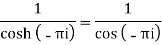
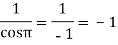
Residue at z=0=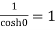

Residue at =

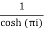
Residue at 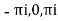are

Respectively -1,1 and -1

Hence the required integrand

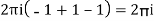
Question-14: Evaluation of definite integrand

Show that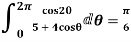 

Sol.

I=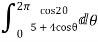

Real part of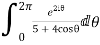

Now I= =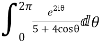

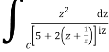
Putting z=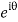 where c is the unit circle |z|=1

I=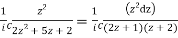

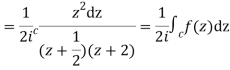
Now f(z) has simple poles at 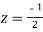and z=-2 of which only 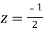lies inside c.

Residue at 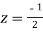is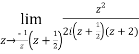 

                      =

=

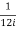
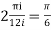
Now equating real parts on both sides we get

I=

1. Prove that

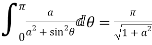
Solution Let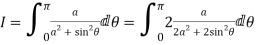

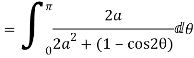
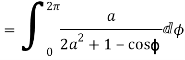
Putting 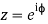where c is the unit circle |z|=1

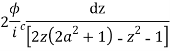
2ai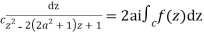

Poles of f(z) are given by the roots of

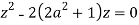
Or

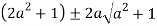
Let

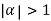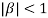Clearly and since we have Hence the only pole inside c is at z=

Residue (at   )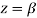

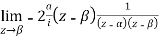
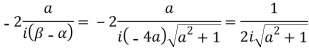
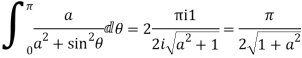
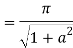
Question-15: Prove that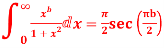

Sol.

Consider

Where c is the contour consisting of a large semicircle in the upper half plane indented at the origin as shown in the figure

Here we have avoided the branch point o, of by indenting the origin

Then only simple of f(z) within c is at z=i

The residue(at z=i) =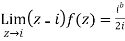

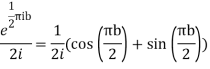
Hence by residue theorem

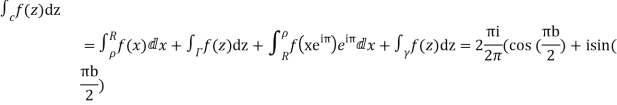
Since 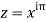on -ve real axis.

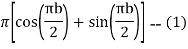
Now

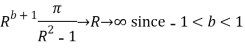
Similarly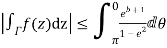 

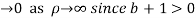
Hence when

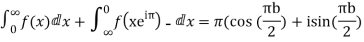
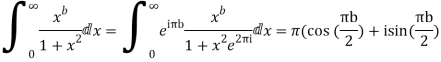
Equating real parts we get

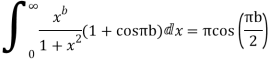
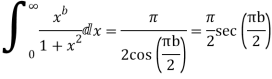
Question-16: Solve the following by cauchy’s integral method:

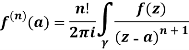
Solution:

Given,

                  =

          =

            =
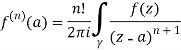
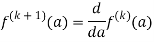